[POI2006]ORK-Ploughing

Description

Byteasar想耕种他那块矩形的田，他每次能耕种矩形的一边（上下左右都行），在他每次耕完后，剩下的田也一定是矩形，每块小区域边长为1，耕地的长宽分别为m和n，不幸的是Byteasar只有一匹老弱的马，从马开始耕地开始，只有当它耕完了一边才会停下休息。但有些地会非常难耕以至于马会非常的累，因此Byteasar需要特别小心。当耕完了一边之后，马可以停下来休息恢复体力。每块地耕种的难度不一，但是Byteasar都非常清楚。我们将地分成m x n块单位矩形——我们用坐标（I,j）来定义它们。每块地都有一个整数T[I,J],来定义（I,j）的耕种难度。所以每次马耕一边地时的难度就是所有它耕种的地的难度总和，对于这匹虚弱的马而言，这个值不能超过他的体力值。Byteasar想知道在马不死掉的情况下最少需要耕多少次才能把地耕完。

Input

第一行三个整数，K,M,N。1<=k<=200 000 000,1<=m,n<=2000.其中K表示马的体力值。

接下来N行每行M个整数表示难度值。（0<=难度值<=10 000）

Output

一个整数表示最少的耕种次数（保证马能耕完）。

Sample Input

12 6 4

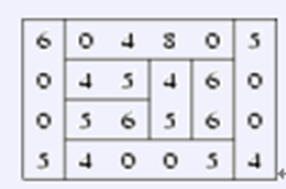
6 0 4 8 0 5

0 4 5 4 6 0

0 5 6 5 6 0

5 4 0 0 5 4

Sample Output

8

题解：贪心

首先，如果确定了最后一次耕地是竖着耕的时候，那么可以确定总共竖着耕了M次（想一想，为什么？）。因此，竖着耕的次数确定了，我们只需要使横着耕的次数最少即可。对此，我们枚举和最后一次竖着耕的那根竖条的上端点高度，则只需要下端点尽量往下延伸即可。 

因此贪心的顺序应该这样：

先贪心左右竖条，能耕则耕，再贪心上横条，最后再贪心下横条，这样的方法必是当前枚举的量中最优的（再想一想，这又是为什么？）。设枚举的上端点为L时，贪心的下端点最下为R。则此时的解为m+n-(r-l+1),如果能更新答案则加入ANS。

我用的是类似记忆化搜索的实现，不过因为贪心竖条，所以只要记录横条的情况l,r，则不必记录竖条情况

同理对于最后一次耕地时横着耕的情况类似。

时间复杂度(n+m)^2；

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int f[][],t2[][],t1[][],k,n,m,a[][],ans;
 int dfs(int l,int r,int L,int R)
 {
     int x1,x2;
     if (f[l][r]!=-) return f[l][r];
     while (L<=R&&t1[L][r]-t1[L][l-]<=k) L++;
     while (L<=R&&t1[R][r]-t1[R][l-]<=k) R--;
     if (L>R)
     {
      f[l][r]=;
       return f[l][r];
     }
    f[l][r]=2e9;
      if (t2[R][l]-t2[L-][l]<=k&&((x1=dfs(l+,r,L,R))!=-))
       f[l][r]=min(f[l][r],x1+);
       if (t2[R][r]-t2[L-][r]<=k&&((x2=dfs(l,r-,L,R))!=-))
       f[l][r]=min(f[l][r],x2+);
      if (f[l][r]==2e9) f[l][r]=-;
      return f[l][r];
 }
 int main()
 {int i,j;
     cin>>k>>m>>n;
     for (i=;i<=n;i++)
     {
         for (j=;j<=m;j++)
         scanf("%d",&a[i][j]);
     }
 for (int i=; i<=n; i++)
         for (int j=; j<=m; j++)
             t1[i][j]=a[i][j]+t1[i][j-],t2[i][j]=a[i][j]+t2[i-][j];
             for (i=;i<=m;i++)
              for (j=;j<=m;j++)
              f[i][j]=-;
       ans=dfs(,m,,n);
       if (ans==-) ans=2e9;
       else ans=ans+n;
     for (int i=; i<=max(n,m); i++)
         for (int j=i+; j<=max(n,m); j++)
             swap(a[i][j],a[j][i]);
     swap(n,m);
     for (int i=; i<=n; i++)
         for (int j=; j<=m; j++)
             t1[i][j]=a[i][j]+t1[i][j-],t2[i][j]=a[i][j]+t2[i-][j];
             for (i=;i<=m;i++)
              for (j=;j<=m;j++)
              f[i][j]=-;
     int x=dfs(,m,,n);
     if (x==-) x=2e9;
     else x=x+n;
     ans=min(ans,x);
     cout<<ans<<endl;
 }