Feign远程调用源码阅读
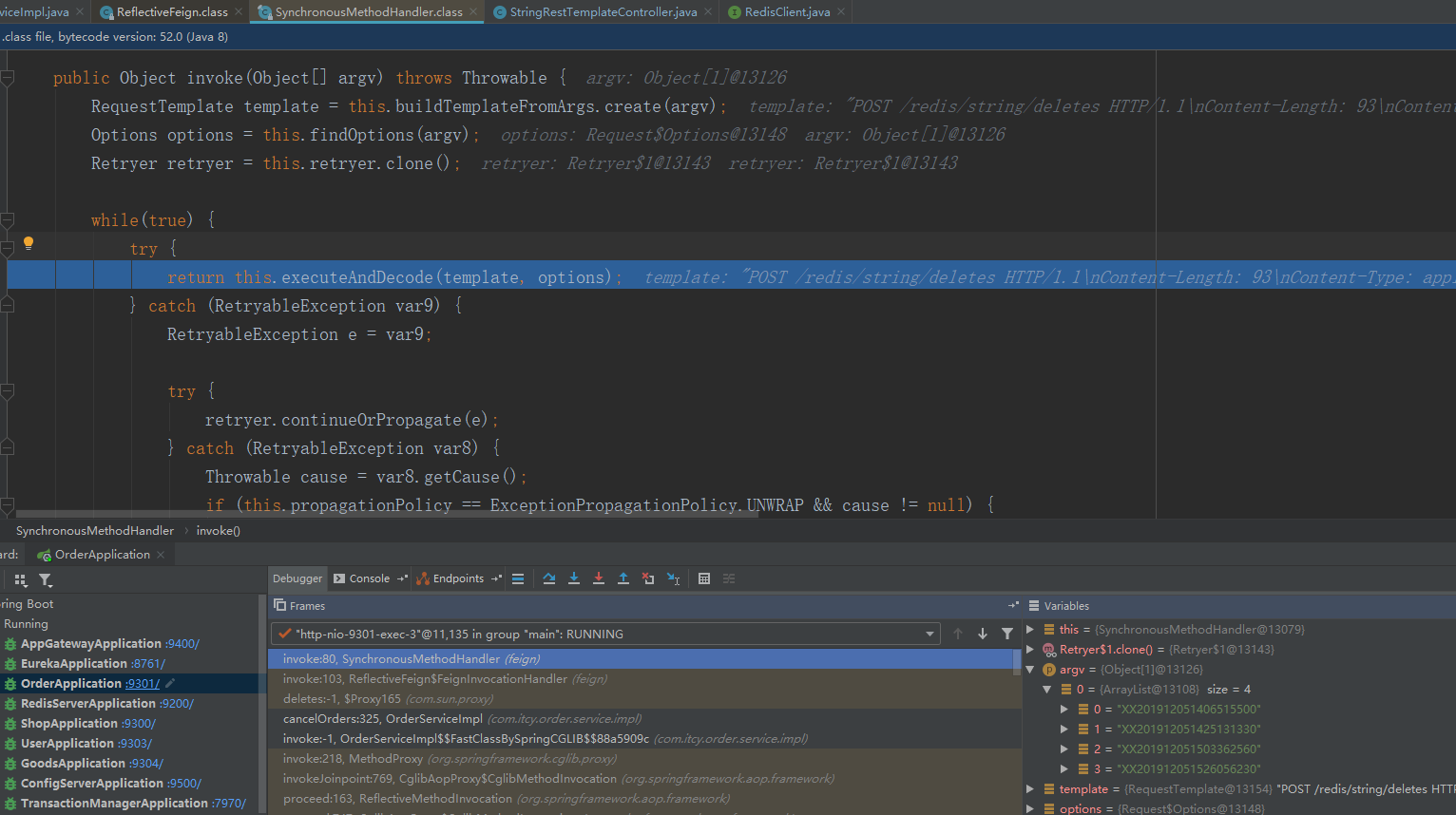

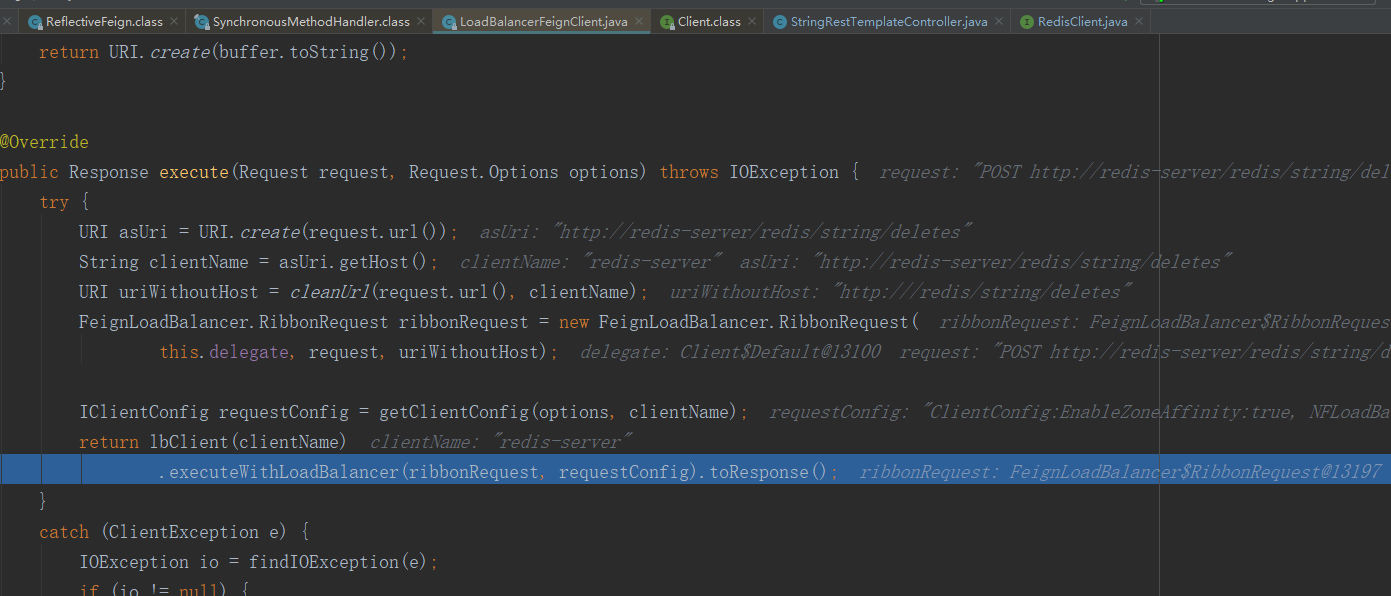
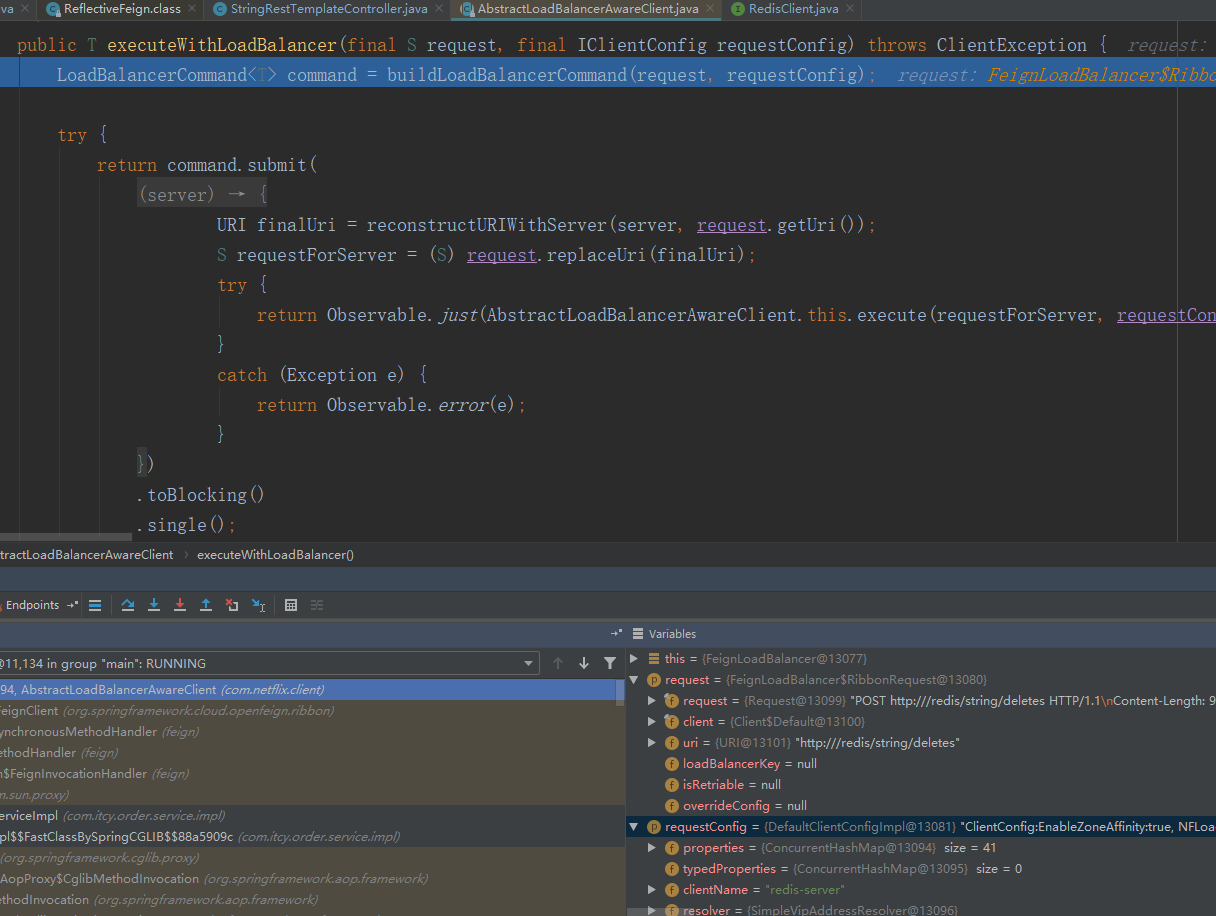
Feign远程调用源码阅读的更多相关文章
- 【Dubbo源码阅读系列】之远程服务调用(上)
今天打算来讲一讲 Dubbo 服务远程调用.笔者在开始看 Dubbo 远程服务相关源码的时候,看的有点迷糊.后来慢慢明白 Dubbo 远程服务的调用的本质就是动态代理模式的一种实现.本地消费者无须知道 ...
- 【Dubbo源码阅读系列】服务暴露之远程暴露
引言 什么叫 远程暴露 ?试着想象着这么一种场景:假设我们新增了一台服务器 A,专门用于发送短信提示给指定用户.那么问题来了,我们的 Message 服务上线之后,应该如何告知调用方服务器,服务器 A ...
- 【原】SDWebImage源码阅读(一)
[原]SDWebImage源码阅读(一) 本文转载请注明出处 —— polobymulberry-博客园 1. 前言 一直没有系统地读过整套源码,就感觉像一直看零碎的知识点,没有系统读过一本专业经典书 ...
- Hive cli源码阅读和梳理
对Cli的重新认识*). hive cli有两种模式, 本地模式: 采用持有的driver对象来处理, 远程模式: 通过连接HiveServer来实现, 由此可见之前的架构图中的描述还是模糊且带有误导 ...
- Spark源码阅读之存储体系--存储体系概述与shuffle服务
一.概述 根据<深入理解Spark:核心思想与源码分析>一书,结合最新的spark源代码master分支进行源码阅读,对新版本的代码加上自己的一些理解,如有错误,希望指出. 1.块管理器B ...
- Rpc框架dubbo-client(v2.6.3) 源码阅读(二)
接上一篇 dubbo-server 之后,再来看一下 dubbo-client 是如何工作的. dubbo提供者服务示例, 其结构是这样的!dubbo://192.168.11.6:20880/com ...
- 【Dubbo源码阅读系列】服务暴露之本地暴露
在上一篇文章中我们介绍 Dubbo 自定义标签解析相关内容,其中我们自定义的 XML 标签 <dubbo:service /> 会被解析为 ServiceBean 对象(传送门:Dubbo ...
- Struts2源码阅读(一)_Struts2框架流程概述
1. Struts2架构图 当外部的httpservletrequest到来时 ,初始到了servlet容器(所以虽然Servlet和Action是解耦合的,但是Action依旧能够通过httpse ...
- Flink源码阅读(1.7.2)
目录 Client提交任务 flink的图结构 StreamGraph OptimizedPlan JobGraph ExecutionGraph flink部署与执行模型 Single Job Jo ...
随机推荐
- Android开发笔记之ArrayAdapter
1,ArrayAdapter的item中的条目的布局文件的正确写法: item.xml <?xml version="1.0" encoding="utf-8&qu ...
- jquery实现表格复选框---多行选择问题(php变量)
1.html多选框标签行 表头的多选框,用于全选,取消全选 <th><input id='allSelected' type="checkbox">< ...
- 【leetcode】969. Pancake Sorting
题目如下: Given an array A, we can perform a pancake flip: We choose some positive integer k <= A.len ...
- vue 父到子动态传值 子组件实时渲染
近期项目中需要一个功能,根据选择不同的 团队片区 id 展示不同的数据,团队id 在父组件 数据在子组件中展示. 根据不同的团队 动态渲染数据总览. 父组件: <Cards ref=" ...
- idea关联git后 Git上传项目提示Push rejected: Push to origin/master was rejected解决办法
当所有的东西都配好以后 就是不上数据 解决方案是在所属右键 点击Git BashHere后 输入:git pull origin master –allow-unrelated-historie ...
- iOS导航栏的背景颜色设置
方法一: (1) self.navigationController.navigationBar.barStyle = UIBarStyleDefault; self.navigationContro ...
- sql INSERT语句
当我们需要向数据库表中插入一条新记录时,就必须使用INSERT语句. INSERT语句的基本语法是: INSERT INTO <表名> (字段1, 字段2, ...) VALUES (值1 ...
- 微信小程序 在使用wx.request时显示加载中
微信小程序中,向后台请求数据是,通常想给用户提示正在加载中,如下图: 我们可以用wx.showLoading(OBJECT),当请求服务器的地方多了,怎么才能不每次都要去调用函数,我们只要对wx.re ...
- 18、webservice使用
1.将axis2.war文件拷到tomcat,webapp文件夹下,然后重启tomcat 访问
- Android逆向之smali语法宝典
0x01.前言 Android采用的是java语言进行开发,但是Android系统有自己的虚拟机Dalvik,代码编译最终不是采用的java的class,而是使用的smali.我们反编译得到的代码,j ...
