Chapter 6 排序

Chapter 6 排序

1-   直接插入排序 O(n²) O(1)

2-   折半插入排序 O(n²) O(1)

适合关键字较多

3-   希尔排序O(nlogn) O(1)

又名，缩小增量排序

4-   冒泡排序O(n²) O(1)

一趟排序后一个关键字到达最终位置

5-   快速排序O(nlogn) O(nlogn)栈

一趟排序后一个关键字到达最终位置

设置一个枢轴，待排序序列越接近无序效率越高

6-   简单选择排序O(n²) O(1)

一趟排序后一个关键字到达最终位置，与初始序列无关。

7-   堆排序O(nlogn) O(1)

可以看成一棵完全二叉树。适合关键字很多，e.g.从10000个挑10个最小的

8-   二路归并排序O(nlogn) O(n)

与初始序列无关

9-   基数排序O(d(n+r_d)) O(r_d)

高位有序，低位有序

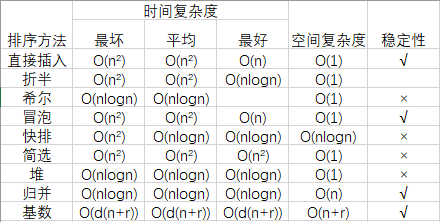
总结：

1   时间复杂度

“快些以nlogn的速度归队”（快排，希尔，归并，堆）

2   空间复杂度

快排O（nlogn）

归并O（n）

基数O（r_d）

3   容易插   直接插入

起的好   冒泡

（都是O(n)，有序）

4   稳定性：考研情绪不稳定，快些选一堆好友聊聊天（快排，希尔，简选，堆）

5   1)一趟排序能保证一个关键字到达最终位置   交换类(2)/选择类(2)

2)关键字比较次数和原始序列无关 ---- 简选，折半

3)排序趟数和原始序列无关 ---- 交换类(2)

直接插入 – 顺序查找

折半插入 – 折半查找

6   内部排序算法应用：

1）n较小：直接插入/简选

2）基本有序：直接插入/冒泡

3）n较大：选择O(nlogn)的“快些归队”

4）n很大：关键字位数较少可分解：基数排序