论文阅读笔记---HetConv

1 写在前边的话

HetConv性能：当使用HetConv取代标准卷积之后，FLOPs大概是之前的1/8到1/3，更重要的是精度几乎不变！！！

论文地址：https://arxiv.org/abs/1903.04120

2 HetConv的结构

实质：是分组卷积与逐点卷积结合的产物。具体如下：

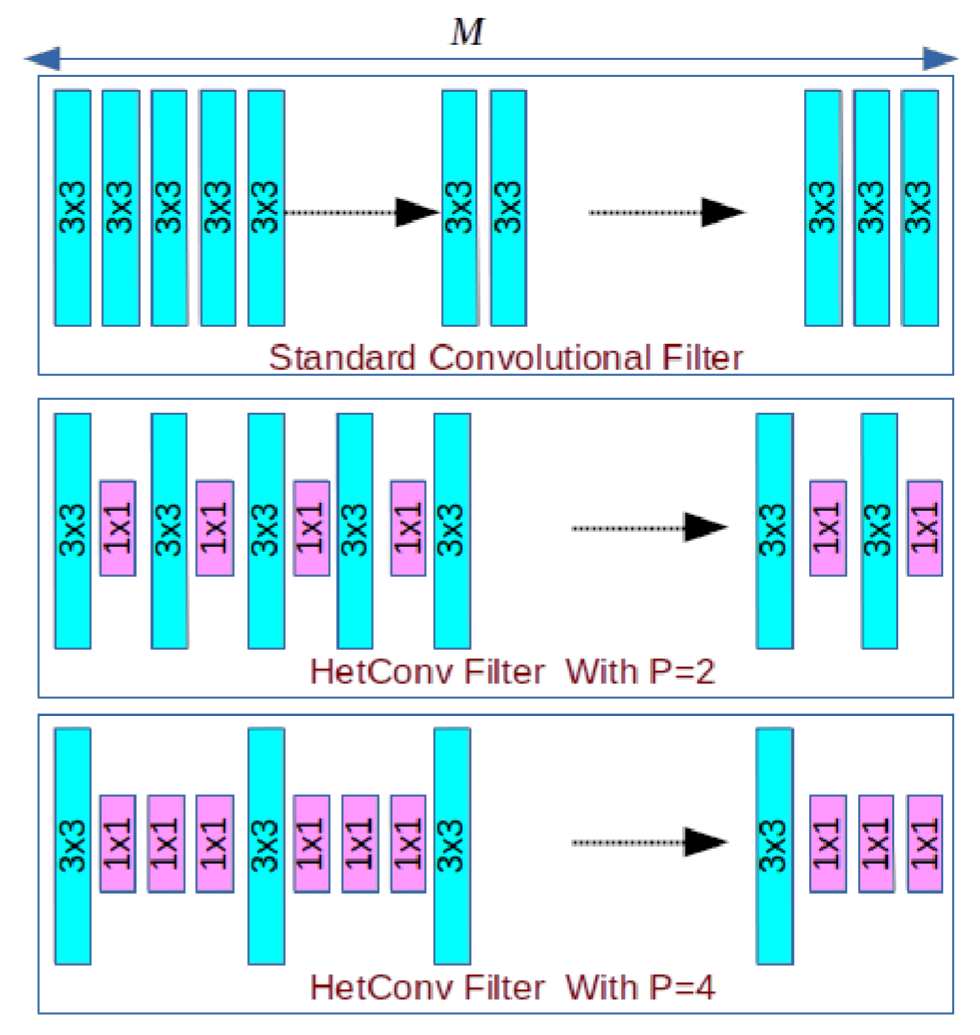
对于卷积（标准卷积；深度卷积；分组卷积；逐点卷积）来讲，每一个filter的尺寸是完全一样的，文章中也称之为同构卷积。

所谓异构卷积，也就是说，对于同一个filter来讲，它的尺寸是不一样的，文章中是有两种。

这样讲可能有点抽象，举个例子来体会一下：

假设原有的一个fliter为：3x3xM，HetConv将M中M/P的3x3卷积核尺寸保留，剩余的M-M/P卷积核尺寸变为1x1的，其中P是一个比例系数。

上边讲的只是一个filter，现假设输出的通道数为N，HetConv是这样做的，假设第一个通道第一个3x3为在第一个位置开始，那么第二个通道中第一个3x3在第二个位置开始，以此类推，如下图所示：

3 计算量比较

假设输入特征图为：\(D_{i} \times D_{i} \times M\)，输出的特征图为：\(D_{o} \times D_{o} \times N\),标准的卷积核为：\(K \times K \times M\)。

对于标准卷积来讲：

计算量为：\(D_{o} \times D_{o} \times M \times N \times K \times K\)

对于异构卷积来讲：

计算量为\(\left(D_{o} \times D_{o} \times M \times N \times K \times K\right) / P\) + \(\left(D_{o} \times D_{o} \times N\right) \times\left(M-\frac{M}{P}\right)\)

异构卷积的计算量/标准卷积的计算量=\(=\frac{1}{P}+\frac{(1-1 / P)}{K^{2}}\)

通过上式中，我们发现，当P=1时，异构卷积就是标准卷积！

对于深度可分离卷积来讲：

计算量为\(D_{o} \times D_{o} \times M \times K \times K+M \times N \times D_{o} \times D_{o}\)

深度可分离卷积的计算量/标准卷积的计算量=\(=\frac{1}{N}+\frac{1}{K^{2}}\)

论文中给出一个极端的case，当P=M时此时效果也比深度可分离卷积好，同时计算量也少，如下所示：

\(\frac{1}{M}+\frac{(1-1 / M)}{K^{2}}<\frac{1}{M}+\frac{1}{K^{2}}\)

对于分组卷积+逐点卷积来讲：

计算量为\(\left(D_{o} \times D_{o} \times M \times N \times K \times K\right) / G+M \times N \times D_{o} \times D_{o}\)

分组卷积+逐点卷积的计算量/标准卷积的计算量=\(\frac{1}{G}+\frac{1}{K^{2}}\)

当P=G时，有：

\(\frac{1}{P}+\frac{(1-1 / P)}{K^{2}}<\frac{1}{P}+\frac{1}{K^{2}}\)

综上所述：

异构卷积比深度可分离卷积，分组卷积计算量都少，并且识别精度还高！

4 代码实现

pytorch实现：https://github.com/sxpro/HetConvolution2d_pytorch