CF572_Div2_D2

题意

http://codeforces.com/contest/1189/problem/D2

---

思考

显然地，如果出现度数为2且两条出边边权不相同的情况，是无法构造合法方案的。

下面考虑缩边后的树，此时每个非叶子节点的度数一定大于等于3。

枚举每个非叶子节点，将其重新作为树的根，并尝试将它所有的出边都达到要求。我们先找到它代表的所有叶子，分两种情况考虑：

1.一条边以下只有一个叶子。如下图所示，红色的路径代表+w/2，w为该边的边权，蓝色路径代表-w/2，能达到平衡。

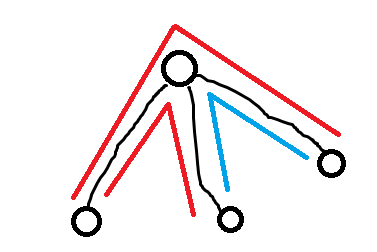
2.一条边以下不止一个叶子。如下图所示，我们要求选定边的子树中挑出的两个叶子的lca的深度必须最大，否则无法消除影响。此处可以挑选dfn最大和最小的那两个。

总复杂度O(n^2)。注意特判一条链的情况。

---

代码

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=2E3+;
 int n;
 int deg[maxn*],hh[maxn];
 int tot,haha;
 bool dot[maxn];
 vector<int>what[maxn];
 vector<int>wait;
 double w[maxn];
 map<pair<int,int>,bool>vis;
 inline pair<int,int>M(int x,int y)
 {
     if(x>y)
         swap(x,y);
     return make_pair(x,y);
 }
 struct edge
 {
     int to,next;
     double w;
 };
 struct note
 {
     int x,y;
     double d;
     note(int a=,int b=,double c=)
     {
         x=a,y=b,d=c;
     }
 };
 vector<note>ans;
 struct graph
 {
     int head[maxn*],size;
     edge E[maxn*];
     inline void add(int u,int v,double w)
     {
         E[++size].to=v;
         E[size].next=head[u];
         E[size].w=w;
         head[u]=size;
     }
     void get(int u,int F,int num)
     {
         for(int i=head[u];i;i=E[i].next)
         {
             int v=E[i].to;
             if(v==F)
                 continue;
             if(u==F)
             {
                 w[++num]=E[i].w;
                 hh[num]=v;
                 get(v,u,num);
             }
             else
                 get(v,u,num);
         }
         if(deg[u]==)
             what[num].push_back(u);
         if(u==F)
             for(int i=;i<=num;++i)
             {
                 if(vis[M(u,hh[i])])
                     continue;
                 if(what[i].size()==)
                 {
                     int u1=what[i][];
                     int x=what[i+<=num?i+:i+-num][];
                     int y=what[i+<=num?i+:i+-num][];
                     double d=w[i]/;
                     ans.push_back(note(u1,x,d));
                     ans.push_back(note(u1,y,d));
                     ans.push_back(note(x,y,-d));
                     vis[M(u,hh[i])]=;
                 }
                 else
                 {
                     int u1=what[i][],u2=what[i][what[i].size()-];
                     int x=what[i+<=num?i+:i+-num][];
                     int y=what[i+<=num?i+:i+-num][];
                     double d=w[i]/;
                     ans.push_back(note(u1,x,d));
                     ans.push_back(note(u2,y,d));
                     ans.push_back(note(u1,u2,-d));
                     ans.push_back(note(x,y,-d));
                     vis[M(u,hh[i])]=;
                 }
             }
     }
     void find(int u,int F,int last)
     {
         dot[u]=;
         if(deg[u]!=)
         {
             haha=last;
             wait.push_back(u);
             return;
         }
         for(int i=head[u];i;i=E[i].next)
         {
             int v=E[i].to;
             if(v==F)
                 continue;
             if(last==)
             {
                 find(v,u,E[i].w);
                 last=E[i].w;
             }
             else if(last==E[i].w)
                 find(v,u,E[i].w);
             else
             {
                 cout<<"NO"<<endl;
                 exit();
             }
         }
     }
     int sum;
     void getsize(int u,int F)
     {
         ++sum;
         for(int i=head[u];i;i=E[i].next)
         {
             int v=E[i].to;
             if(v==F)
                 continue;
             getsize(v,u);
         }
     }
 }source,G;
 int main()
 {
     ios::sync_with_stdio(false);
     cin>>n;
     for(int i=;i<=n;++i)
     {
         int x,y;
         double z;
         cin>>x>>y>>z;
         source.add(x,y,z);
         source.add(y,x,z);
         ++deg[x],++deg[y];
     }
     int P1=,P2=;
     for(int u=;u<=n;++u)
     {
         if(deg[u]==)
         {
             if(!dot[u])
             {
                 source.find(u,u,);
                 wait.clear();
                 G.add(wait[],wait[],haha);
                 G.add(wait[],wait[],haha);
                 P1=wait[],P2=wait[];
             }
             continue;
         }
         for(int i=source.head[u];i;i=source.E[i].next)
         {
             int v=source.E[i].to;
             haha=source.E[i].w;
             if(deg[v]!=)
                 G.add(u,v,source.E[i].w);
         }
     }
     cout<<"YES"<<endl;
     G.getsize(P1,P1);
     if(G.sum==)
     {
         cout<<<<endl;
         cout<<P1<<" "<<P2<<" "<<haha<<endl;
         return ;
     }
     for(int u=;u<=n;++u)
     {
         if(deg[u]==)
             continue;
         for(int i=;i<=n;++i)
             what[i].clear();
         G.get(u,u,);
     }
     int del=;
     for(int i=;i<ans.size();++i)
         if(abs(ans[i].d-)<=0.01)
             ++del;
     cout<<ans.size()-del<<endl;
     for(int i=;i<ans.size();++i)
         if(abs(ans[i].d-)>0.01)
             cout<<ans[i].x<<" "<<ans[i].y<<" "<<ans[i].d<<endl;
     return ;
 }