Codeforces Hello2020 A-E简要题解

contest链接：https://codeforces.com/contest/1284

A. New Year and Naming

思路：签到，字符串存一下，取余拼接。

 #include<iostream>
 #include<vector>
 #include<cstring>
 #include<map>
 #include<algorithm>
 using namespace std;
 const int maxn = 1e+;
 int main(){
     vector<string> s1;
     vector<string> s2;
     int n,m;cin>>n>>m;
     for(int i = ;i<n;i++){
         string t;cin>>t;
         s1.push_back(t);
     }
     for(int i = ;i<m;i++){
         string t;cin>>t;
         s2.push_back(t);
     }
     int q;cin>>q;
     while(q--){
         long long y;cin>>y;
         cout<<s1[(y-)%n]+s2[(y-)%m]<<endl;
     }
     return ;
 }

B. New Year and Ascent Sequence

题意：定义上升序列Ascent,在一组序列A中，存在1<i<j<n，使得Ai<Aj。现在给定n个序列，求n个序列两两组合的n^2个组合序列中，有多少个组合是Ascent序列。。

思路： 用两个MAX,MIN数组分别记录下每个序列的最大值和最小值，然后把最大值进行排序。每次做一遍二分，取每个数组中的最小值到所有数组中的最大值中找有多少个数比它大，这样组合的新序列便是满足Ascent性质。如果本身这个序列就已经满足Ascent的性质，那么直接把最大值设置为9999999，最小值设置为-1存进去。

 #include<iostream>
 #include<vector>
 #include<cstring>
 #include<map>
 #include<algorithm>
 using namespace std;
 vector<int> MAX;
 vector<int> MIN;
 int main(){
     int t;
     cin>>t;
     for(int i = ;i<t;i++){
         int Length;
         cin>>Length;
         long long Min = ;
         long long Max = -;
         int ok = ;
         for(int j = ;j<Length;j++){
             long long cur;
             cin>>cur;
             if(cur> Min && ok == ){
                 ok = ;
             }
             Min = min(Min,cur);
             Max = max(Max,cur);
         }
         if(ok == ){
             MAX.push_back(Max);
             MIN.push_back(Min);
         }
         else{
             MAX.push_back();
             MIN.push_back(-);
         }
     }
     sort(MAX.begin() ,MAX.end() );
     long long ans = ;
     for(int i = ;i<t;i++){
         ans+=(MAX.end() -upper_bound(MAX.begin() ,MAX.end() ,MIN[i]));
         //cout<<ans<<endl;
     }
     cout<<ans;
     return ;
 }

C. New Year and Permutation

题意：定义一个framed segment，在区间[l,r]中，max值-min值 = r - l。求有1-n 组成的序列中，所有framed segment的个数%m

思路：组合数学推一个结论。例如假设1到n组成的序列中，求长度为k的framed segment，那么其一段序列的最大值 - 最小值 = k，例如n = 5,k = 3，这些framed segment 必定是 1 2 3 或者2 3 4 或者 3 4 5，可以观测到其长度为k的framed segment必定是连续的，可以把他们单独算一个整体，这样序列总体长度变为n - k + 1，内部长度为k，内部组合种类就是k!个，总体组合种类就是(n-k+1)！，长度为k的framed segment种类又是（123，234，345）n - k + 1种，所以长度为k的framed segment 最终答案就是(n-k+1)*(n-k+1)!*k!，预处理一下阶乘即可。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 typedef long long ll;
 const int maxn = 2e5+5e4+;
 ll fac[maxn];
 int main(){
     ll n,m;
     cin>>n>>m;
     fac[] = ;
     for(int i = ;i<=n;i++){
         fac[i] = (fac[i-]*i)%m;
     }
     ll ans = ;
     for(int i = ;i<=n;i++){
         ans +=((n+-i)*(fac[i])%m)*(fac[n+-i])%m;
         ans = ans%m;
     }
     // 1 2 3
     cout<<ans%m;
     return ;
 }

D. New Year and Conference

题意：有n场讲座，有两个场地a和b，如果在a场地开讲座则需要占用[sai,eai],在b场地开讲座则需要占用[sbi,ebi]这个时间段,假如开两场讲座,如果在a场地开不冲突,而b场地开冲突,则称其为敏感的，同理a和b反过来也是一样的,如果ab两场地都冲突则也不是敏感的，先求给定的n场讲座,任意的两两讲座是否在ab场地敏感。

思路：暴力枚举是O（n^2）复杂度，必定超时，这里可以用线段树或ST表做，达到一个nlogn的复杂度。对于任意一个讲座x，找出所有与x讲座在a场地冲突的讲座，再判断其是否在b场地冲突，如果不是则直接输出“NO”

首先对所有讲座的sa和ea进行升序（sa为a场地开始时间，ea为a场地结束时间，sb和eb就是b场地开始结束时间），例如讲座 i 的时间片是[x,y]，在其时间片上与 i 在a场地冲突的讲座用二分的方法可以枚举出来一个离散化后的区间，然后我们用线段树维护b场地的sb最大值和eb最小值，每次查询出这个区间的的sb最大值和eb最小值，此时如果说sb最大值 > y 或者 eb最小值 < x,那么这些表演中必定存在b场地与表演i不冲突的情况，此时直接输出“NO”，把所有的讲座都check一遍，交换ab次序再check即可，上述只检验了在a场地冲突一定在b场地冲突的情况，但并未考虑在b场地冲突而在a场地不冲突的情况。

总体时间复杂度nlogn。

AC代码:

 #include<iostream>
 #include<vector>
 #include<cstdlib>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<map>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e5+;
 struct node{
     int sa,ea,sb,eb;
     node(){};
     node(int a,int b,int c,int d){
         sa = a,ea = b,sb = c,eb = d;
     }
     bool operator<(node cur)const{
         if(sa == cur.sa ) return ea<cur.ea ;
         return sa < cur.sa ;
     }
 }point[maxn];
 int segt_max[*maxn],segt_min[*maxn];
 void build(int l,int r,int k){//建两个线段树维护区间最大最小值
     if(l == r) {
         segt_max[k] = point[l].sb;
         segt_min[k] = point[l].eb;
         return ;
     }
     int mid = (l+r)/;
     build(l,mid,*k);
     build(mid+,r,*k+);
     segt_max[k] = max(segt_max[*k],segt_max[*k+]);
     segt_min[k] = min(segt_min[*k],segt_min[*k+]);
 }
 int queryMin(int l,int r,int al,int ar,int k){//查询区间最小值
     if(l >= al && r <= ar) return segt_min[k];
     int mid = (l+r)/;
     if(ar<=mid) return queryMin(l,mid,al,ar,*k);
     else if(al>mid){
         return queryMin(mid+,r,al,ar,*k+);
     }
     else {
         return min(queryMin(l,mid,al,mid,*k),queryMin(mid+,r,mid+,ar,*k+));
     }
 }
 int queryMax(int l,int r,int al,int ar,int k){//查询区间最大值
     if(l >= al && r <= ar) return segt_max[k];
     int mid = (l+r)/;
     if(ar<=mid) return queryMax(l,mid,al,ar,*k);
     else if(al>mid){
         return queryMax(mid+,r,al,ar,*k+);
     }
     else {
         return max(queryMax(l,mid,al,mid,*k),queryMax(mid+,r,mid+,ar,*k+));
     }
 }
 bool check(int n){
     sort(point+,point++n);
     build(,n,);
     for(int i = ;i<=n;i++){
         int pos = lower_bound(point+,point++n,node(point[i].ea ,1e9+,,))-point-;
         //查找与第i场演讲冲突的集合
         if(i+>pos) continue;//无冲突直接跳过
         //check一下另一个场地的所有表演是否都冲突
         if(queryMin(,n,i+,pos,)<point[i].sb || queryMax(,n,i+,pos,)>point[i].eb){
             return false;
         }
     }
     return true;
 }
 int main()
 {
     int n;
     cin>>n;
     int f = ;
     for(int i = ;i<=n;i++){
         cin>>point[i].sa>>point[i].ea>>point[i].sb>>point[i].eb;
     }
     if(check(n)) f++;
     for(int i = ;i<=n;i++){
         swap(point[i].sa,point[i].sb);
         swap(point[i].ea,point[i].eb);
     }
     if(check(n)) f++;
     if(f == ) cout<<"YES";
     else cout<<"NO";
     return ;
 }

E. New Year and Castle Construction

题意：平面上有ｎ个点，问你存在多少组四个点围成的四边形 严格包围某个点P的情况。不存在三点共线。

思路：首先看数据范围是2500，可以做n^2的枚举，我们可以枚举两遍n。正面求解有些困难，反面求解可以考虑有多少组子集不满足题目要求，拿总的子集数量减去不满足的就是答案。

那么考虑不满足题意的点集。

首先如果对于一对点P和P1，让它们连线，以P为基准，相对度数为0度，枚举P和P1这个条线以上的所有点，假设枚举出n个点，n个点加P1,从中选出4个点，这4个点组成的四边形必定不含点P，以此性质就可以做了。

首先做一遍极角排序，然后固定一条边，以这条边为0度，开始扫描这条边0到180度的所有点，然后从中任意选出3个点C（n,3），与P1组成的四边形便不封闭包围P1，统计所有不满足条件的点集，用总体点集

个数C（n,5）- 不满足的组合个数 就是答案。

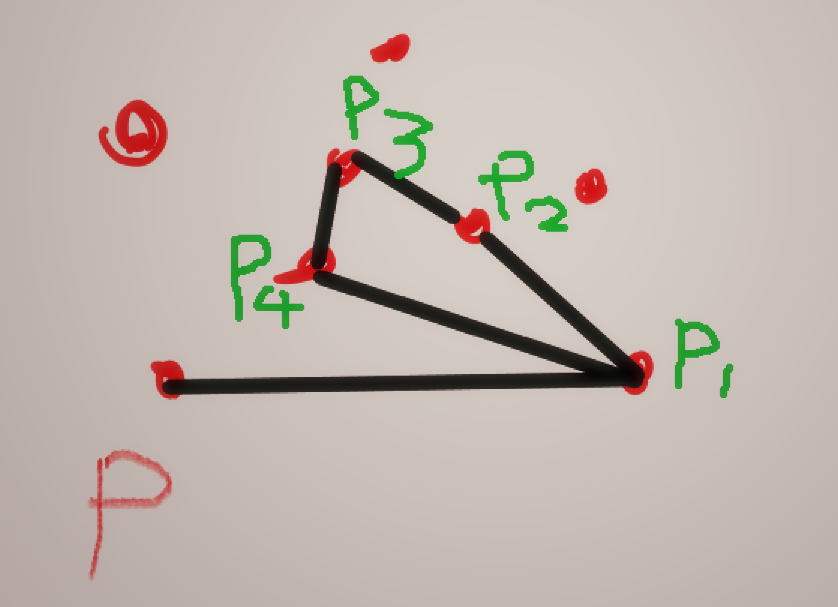
如图所示，P1,P2,P3,P4组成的四边形不封闭包围点P。

AC代码：

 #include<iostream>
 #include<vector>
 #include<cstdlib>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<map>
 using namespace std;
 typedef long long ll;
 const long double pi = acos(-.0L);
 const int maxn = 2e3+;
 long double x[maxn],y[maxn];
 int main()
 {
     int n;cin>>n;
     ll ans = (ll)n*(n-)*(n-)*(n-)*(n-)/; //计算C(n,5)
     for(int i = ;i<n;i++){
         ll xi,yi;
         cin>>xi>>yi;
         x[i] = xi,y[i] = yi;
     }
     for(int i = ;i<n;i++){
         vector<long double> v;
         for(int j = ;j<n;j++){
             if(i == j) continue;
             v.push_back(atan2(y[j]-y[i],x[j]-x[i])); //算一下角度
         }
         sort(v.begin(),v.end());//做极角排序
         int k = n -  , cur = ;
         for(int j = ;j<k;j++){
             while(cur < j+k){ //枚举点个数增加一倍
                 long double angle = v[cur%k] - v[j];//枚举两条边的夹角
                 if(angle < ) angle+=*pi;//如果角度小于0,则增加2*pi转一圈
                 if(angle < pi) cur++;//如果该点在枚举的这条线上面，则cur++
                 else break;
             }
             long long cnt = cur - j - ;
             ans-=1ll*cnt*(cnt-)*(cnt-)/;
         }
     }
     cout<<ans;
     return ;
 }