bzoj 2427 软件安装 - Tarjan - 树形动态规划

题目描述

现在我们的手头有N个软件，对于一个软件i，它要占用W_i的磁盘空间，它的价值为V_i。我们希望从中选择一些软件安装到一台磁盘容量为M计算机上，使得这些软件的价值尽可能大（即V_i的和最大）。

但是现在有个问题：软件之间存在依赖关系，即软件i只有在安装了软件j（包括软件j的直接或间接依赖）的情况下才能正确工作（软件i依赖软件j)。幸运的是，一个软件最多依赖另外一个软件。如果一个软件不能正常工作，那么它能够发挥的作用为0。

我们现在知道了软件之间的依赖关系：软件i依赖软件D_i。现在请你设计出一种方案，安装价值尽量大的软件。一个软件只能被安装一次，如果一个软件没有依赖则D_i=0，这时只要这个软件安装了，它就能正常工作。

输入

第1行：N, M  （0<=N<=100, 0<=M<=500）
      第2行：W₁, W₂, ... W_i, ..., W_n （0<=W_i<=M ）
      第3行：V₁, V₂, ..., V_i, ..., V_n  （0<=Vi<=1000 ）
      第4行：D₁, D₂, ..., D_i, ..., D_n（0<=D_i<=N, D_i≠i ）

输出

一个整数，代表最大价值。

样例输入

3 10
5 5 6
2 3 4
0 1 1

样例输出

5

来源

Day2

（转自http://www.lydsy.com/JudgeOnline/problem.php?id=2427）

---

　　这道题看起来像是树归，首先来判断一下，一个软件只能依赖于一个软件，正如树，一个节点只有一个父节点（除了根节点）（把所有节点都连接到0号节点下），但是来构思一组数据:

　　D：

　　像这样，1依赖于2，2依赖于3.，3依赖于1，构成了一个环（强连通分量），明显不符合树的性质，但是仔细想想，要么全选要么全不选

就可以把它当成一个节点来看待。

　　至于缩点。。。这个也比较简单，和codevs上"爱在心中"差不多，首先给belong数组赋初值：

for(int i = ;i <= n;i++)
belong[i] = i;

　　再Tarjan一次，将元素弹出栈时要将对应belong数组中这个强连通分量的值全部设成这中间任意元素的值（但必须一样）

接着for循环扫描一次，凡是belong[i] != i的像这样处理一下:

w[belong[i]] += w[i];
v[belong[i]] += v[i];

　　如果出现访问d[i]就像这样访问:

d[belong[i]]......

　　是不是十分方便快捷？（除了Tarjan算法的代码复杂度）

　　下面思考一下树归方程，感觉如果玩多叉树的话状态很多，就转成二叉树，为了代码简洁，有这么两种方法

第一种方法是记录每个节点添加进的"兄弟"的地址，就加一个指针变量，添加一个"儿子"或者"兄弟"时,就访问

这个对应的指针变量，先正常加入，然后把指针指向它

for(int i = ;i <= n;i++){
    for(int j = head[i];j;j = edge[j].next){
        if(belong[i] == i && belong[i] != belong[edge[j].end]){
            if(node[i]->left != NULL)
                node[i]->left->bro = &node[edge[belong[j]].end];
            else node[i]->left = &node[edge[belong[j]].end];;
        }
    }
}

　　是不是显得有点麻烦？而且严重牺牲了可读性，在看了某大神的代码后，我知道了这种方法:

用bro[i]储存i节点的右子树(原先的"兄弟"),用son[i]储存i节点的左子树(原先的"子节点")，

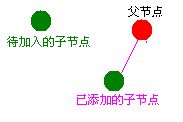
然后：

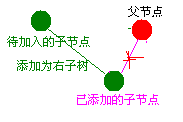
最后：

代码实现也比较简单：

for(int i = ;i <= n;i++){
    for(int j = head[i];j;j = edge[j].next){
        if(belong[i] == i && belong[i] != belong[edge[j].end]){
            bro[i] = son[belong[edge[j].end]];
            son[belong[edge[j].end]] = i;
        }
    }
}

　　另外关于左右子树出现空的时候，如果多加几个if语句的话，可能树形DP的代码就和Tarjan算法有的一拼了，可以把

它的左右子树的位置设成一个值为0的节点，这就相当于一个空节点，但并不影响计算结果

　　写出树归方程:

f[index][i] = max(f[index][i],v[index] + f[left][j] + f[right][limit - j]);

（index是第index个节点，limit是i - w[i],left = son[index],right = bro[index]）

最后附上我超级不简洁的代码（如果想要速度更快，可以把cin，cout改成scanf和printf）

Code:

 /**
  * bzoj
  * Problem#2427
  * Accepted
  * Time:220ms
  * Memory:1492k
  */
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<stack>
 #include<vector>
 #define _min(a,b) ((a)<(b))?(a):(b)
 using namespace std;
 typedef bool boolean;
 typedef class Edge{
     public:
         int end;
         int next;
         Edge():end(),next(){}
         Edge(int end,int next):end(end),next(next){}
 }Edge;
 Edge *edge;
 int n,m;
 int *w;        //软件大小
 int *v;        //价值
 int *d;
 int *head;
 int top;
 inline void addEdge(int from,int end){
     top++;
     edge[top].next=head[from];
     edge[top].end=end;
     head[from]=top;
 }
 boolean *visited;
 int *visitID;
 int *exitID;
 int entryed;
 stack<int> sta;
 int *belong;
 boolean *inStack;
 int *bro;
 int *son;
 void getSonMap(int end){
     int now=-;
     int exits=;
     while(now!=end){
         now=sta.top();
         belong[now]=end;
         inStack[now]=false;
         exits++;
         sta.pop();
     }
 }
 void Tarjan(const int pi){
     int index=head[pi];
     visitID[pi]=++entryed;
     exitID[pi]=visitID[pi];
     visited[pi]=true;
     inStack[pi]=true;
     sta.push(pi);
     while(index!=){
         if(!visited[edge[index].end]){
             Tarjan(edge[index].end);
             exitID[pi]=_min(exitID[pi],exitID[edge[index].end]);
         }else if(inStack[edge[index].end]){
             exitID[pi]=_min(exitID[pi],visitID[edge[index].end]);
         }
         index=edge[index].next;
     }
     if(exitID[pi]==visitID[pi]){
         getSonMap(pi);
     }
 }
 void rebuild(){
     vector<int> indexs;
     for(int i=;i<=n;i++){
         if(belong[i] != i){
             v[belong[i]] += v[i];
             w[belong[i]] += w[i];
             indexs.push_back(belong[i]);
         }
     }
     for(int i = ;i < indexs.size();i++)
         edge[head[indexs[i]]].end = ;
 }
 void create(){
     bro = new int[(const int)(n + )];
     son = new int[(const int)(n + )];
     for(int i = ;i <= n;i++){
         son[i] = n + ;
         bro[i] = n + ;
     }
     for(int i = ;i <= n;i++){
         for(int j = head[i];j;j = edge[j].next){
             if(belong[i] == i && belong[i] != belong[edge[j].end]){
                 bro[i] = son[belong[edge[j].end]];
                 son[belong[edge[j].end]] = i;
             }
         }
     }
 }
 int f[][];
 void solve(int index){
     if(index > n) return ;
     solve(son[index]);
     solve(bro[index]);
     int left = son[index];
     int right = bro[index];
     for(int i = ;i <= m;i++){
         f[index][i] = max(f[index][i],f[right][i]);
         int limit = i - w[index];
         for(int j = ;j <= limit;j++){
             f[index][i] = max(f[index][i],v[index] + f[left][j] + f[right][limit - j]);
         }
     }
 }
 int main(){
     cin>>n>>m;
     head=new int[(const int)(n+)];
     edge=new Edge[(const int)(n+)];
     visited=new boolean[(const int)(n+)];
     visitID=new int[(const int)(n+)];
     exitID =new int[(const int)(n+)];
     belong =new int[(const int)(n+)];
     inStack=new boolean[(const int)(n+)];
     memset(head,,sizeof(int)*(n+));
     memset(visited,false,sizeof(boolean)*(n+));
     memset(inStack,false,sizeof(boolean)*(n+));
     w = new int[(const int)(n + )];
     v = new int[(const int)(n + )];
     d = new int[(const int)(n + )];
     for(int i=;i<=n;i++)
         scanf("%d",&w[i]);
     for(int i = ;i <= n;i++)
         scanf("%d",&v[i]);
     for(int i = ;i <= n;i++){
         scanf("%d",&d[i]);
         addEdge(i, d[i]);
     }
     for(int i=;i<=n;i++) belong[i]=i;
     for(int i=;i<=n;i++){
         if(!visited[i])
             Tarjan(i);
     }
     delete[] visited;
     delete[] inStack;
     rebuild();
     delete[] exitID;
     delete[] visitID;
     create();
     w[] = ;
     v[] = ;
     solve();
     printf("%d",f[][m]);
     return ;
 }