LCA

2016.1.28

LCA，就是最近公共祖先，这里介绍倍增的算法。

首先我们要预处理，设f[i][j]为编号为i的节点的2^j级祖先，所谓2^j级祖先，就是从i节点开始往树的上层数2^j个节点。如下图所示

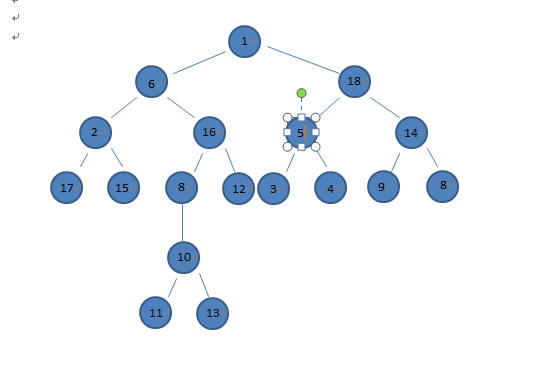编号是乱编的。。。

节点11的2⁰级祖先就是他爹10号节点，节点11的2¹级祖先就是8号节点，节点11的2²级祖先就是6号节点。

这样我们就有递归式：f[i][j]=f[ f[i][j-1] ][ j-1 ],i号节点的2^j级祖先就是i号节点的2^j-1级祖先的2^j-1级祖先。

这件事情我们可以通过从根节点进行一次dfs来完成，在递归之前处理当前结点的祖先即可。

代码如下：

void LCA(int x)
{
    vis[x]=;
    for(int i=;(<<i)<=dep[x];i++)
    {
        int c=f[x][i-];//c为x的2^i-1级祖先
        f[x][i]=f[c][i-];//f[x][i]赋值为c的2^i-1级祖先
    }
    for(int i=final[x];i;i=last[i])
    {
        if(!vis[to[i]])
        {
            dep[to[i]]=dep[x]+;//更新深度
            f[to[i]][]=x;//更新该边到达节点的2^0级祖先
            LCA(to[i]);
        }
    }
}

然后，我们对于询问的节点a和b的最近公共祖先，开始倍增。具体操作如下：（假设在11号和3号节点各站了一个小人a和b）

1、让深度较大的节点（假设是上图11号节点）上的小人沿着边一直向上层跳到和深度较小的节点（假设是上图3号节点）同一深度。（也就是a跳到8号节点）

2、a和b同时开始倍增，如果倍增之后两人所在位置不同，即执行倍增，否则，减小倍增的倍数（假设倍增2^k后发现两人在同一位置了，则尝试倍增2^k-1）。

3、重复执行操作2，直到无法继续执行。

4、现在，a一定6号节点，b一定在18号节点。换句话说，a和b一定在他俩lca的下一层。

5、a和b往上跳一层便是他俩的lca了

这段操作并不好理解，对着代码看就好了:

int query(int a,int b)
{
    if(dep[a]<dep[b]) swap(a,b);
    for(int i = maxlog ; i >=  ; i-- ) //2^maxlog是这棵树的最大可能深度，从大级别往小级别倍增，直到a跳到与b同深度
        if(dep[a]-(<<i)>=dep[b])
            a=f[a][i];
    if(a==b) return b;//注意特判，b可能就是他俩的lca
    for(int i = maxlog ; i >=  ; i-- ) //a和b同时开始往上倍增
        if(dep[a] > (<<i) && f[a][i] != f[b][i])
        {
            a=f[a][i];
            b=f[b][i];
        }
    //此时a和b的上一层就是lca
    return f[a][];
}

然后再来看题：NOIP201307货车运输

BZOJ 3732 Network