POJ2779 线性DP 或 杨氏三角 和 钩子公式

POJ2779 线性DP 或 杨氏三角 和 钩子公式

本来就想回顾一下基础的线性DP谁知道今早碰到的都是这种大难题，QQQQ，不会

这个也没有去理解线性DP的解法，了解了杨氏三角和钩子公式，做出了POJ2779

杨氏矩阵和勾长公式

杨氏矩阵又叫杨氏图表，它是这样一个矩阵，满足条件：

(1)如果格子(i,j)没有元素，则它右边和上边的相邻格子也一定没有元素。

(2)如果格子(i,j)有元素a[i][j]，则它右边和上边的相邻格子要么没有元素，要么有元素且比a[i][j]大。

1 ~ n所组成杨氏矩阵的个数可以通过下面的递推式得到：

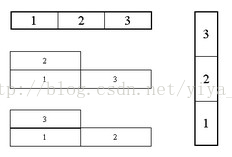
如图就是n=3时的杨氏矩阵。

 

下面介绍一个公式，那就是著名的钩子公式。

对于给定形状，不同的杨氏矩阵的个数为：n！除以每个格子的钩子长度加1的积。其中钩子长度定义为该格子

右边的格子数和它上边的格子数之和。

钩子公式：res=n!  /  (hock[1]*hock[2]*.....hock[n]);

hock[i]=在其上方和右方的所有个数+1；

reference : 咿呀而已

知道了这个就能后解出来了

奥，有一个地方要注意就是res=n!  /  (hock[1]*hock[2]*.....hock[n]);

为了防止分子或分母的越界情况，要进行单一元素的约分化简；很好理解看代码就ok

#include <iostream>
#include <cstdio>
#include <string.h>
using namespace std;
int gcd(int a,int b)
{
    return b ==  ? a : gcd(b,a % b);
}

int d[];
int num[];

int main()
{
    int n;
    while(~scanf("%d",&n) && n)//行数
    {
        for(int i = ;i <= n;i++)
        {
            scanf("%d",&d[i]);//行长度
        }
        int tot = ;
        memset(num,,sizeof(num));
        //计算hock值————
        long long t1,t2;
        for(int i = ;i <= n;i++)//遍历行数
        {
            for(int j = ;j <= d[i];j++)//遍历行上的铜须
            {
                tot++;
                num[tot] += d[i] - j + ;//应该求右面
                for(int k = i + ;k <= n;k++)//和下面的看后面的同学有没有满足的
                {
                    if(d[k] >= j)
                    {
                        num[tot]++;
                    }
                    else////如果紧靠的都没有，下面的更不会有
                    {
                        break;
                    }

                }
            }
        }
        //代入钩子公式——互相约分一下
        t1 = ;
        t2 = ;
        for(int i = ;i <= tot;i++)
        {
            t1 *= i;
            t2 *= num[i];
            int t = gcd(t1,t2);
            t1 /= t;
            t2 /= t;
        }
        printf("%lld\n",t1 / t2);

    }return ;
}

#include <iostream>
#include <cstdio>
#include <string.h>
using namespace std;
int gcd(int a,int b)
{
    return b ==  ? a : gcd(b,a % b);
}

int d[];
int num[];

int main()
{
    int n;
    while(~scanf("%d",&n) && n)//行数
    {
        for(int i = ;i <= n;i++)
        {
            scanf("%d",&d[i]);//行长度
        }
        int tot = ;
        memset(num,,sizeof(num));
        //计算hock值————
        long long t1,t2;
        for(int i = ;i <= n;i++)//遍历行数
        {
            for(int j = ;j <= d[i];j++)//遍历行上的铜须
            {
                tot++;
                num[tot] += d[i] - j + ;//应该求右面
                for(int k = i + ;k <= n;k++)//和下面的看后面的同学有没有满足的
                {
                    if(d[k] >= j)
                    {
                        num[tot]++;
                    }
                    else////如果紧靠的都没有，下面的更不会有
                    {
                        break;
                    }

                }
            }
        }
        //代入钩子公式——互相约分一下
        t1 = ;
        t2 = ;
        for(int i = ;i <= tot;i++)
        {
            t1 *= i;
            t2 *= num[i];
            int t = gcd(t1,t2);
            t1 /= t;
            t2 /= t;
        }
        printf("%lld\n",t1 / t2);

    }return ;
}