Java实现二叉树先序，中序，后序，层次遍历

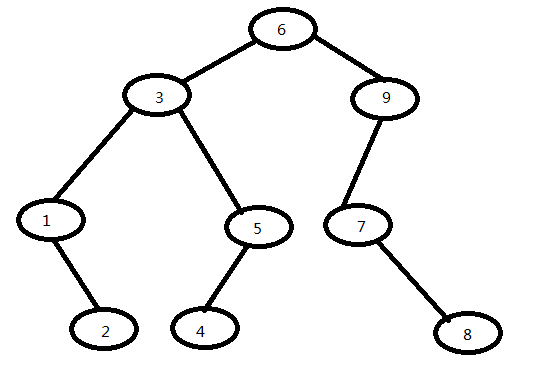
一、以下是我要解析的一个二叉树的模型形状。本文实现了以下方式的遍历：

1、用递归的方法实现了前序、中序、后序的遍历；

2、利用队列的方法实现层次遍历；

3、用堆栈的方法实现前序、中序、后序的遍历。

。

二、遍历

1、首先创建节点类

public class Node {
    private int data;
    private Node leftNode;
    private Node rightNode;
    public Node(int data, Node leftNode, Node rightNode){
        this.data = data;
        this.leftNode = leftNode;
        this.rightNode = rightNode;
    }  

    public int getData() {
        return data;
    }
    public void setData(int data) {
        this.data = data;
    }
    public Node getLeftNode() {
        return leftNode;
    }
    public void setLeftNode(Node leftNode) {
        this.leftNode = leftNode;
    }
    public Node getRightNode() {
        return rightNode;
    }
    public void setRightNode(Node rightNode) {
        this.rightNode = rightNode;
    }
}

2、递归方式实现前序、中序、后续遍历

public class BinaryTree {
    /**
     * @author yaobo
     * 二叉树的先序中序后序排序
     */
    public Node init() {//注意必须逆序建立，先建立子节点，再逆序往上建立，因为非叶子结点会使用到下面的节点，而初始化是按顺序初始化的，不逆序建立会报错
        Node J = new Node(8, null, null);
        Node H = new Node(4, null, null);
        Node G = new Node(2, null, null);
        Node F = new Node(7, null, J);
        Node E = new Node(5, H, null);
        Node D = new Node(1, null, G);
        Node C = new Node(9, F, null);
        Node B = new Node(3, D, E);
        Node A = new Node(6, B, C);
        return A;   //返回根节点
    }

    public void printNode(Node node){
        System.out.print(node.getData());
    }
    public void theFirstTraversal(Node root) {  //先序遍历
        printNode(root);
        if (root.getLeftNode() != null) {  //使用递归进行遍历左孩子
            theFirstTraversal(root.getLeftNode());
        }
        if (root.getRightNode() != null) {  //递归遍历右孩子
            theFirstTraversal(root.getRightNode());
        }
    }
    public void theInOrderTraversal(Node root) {  //中序遍历
        if (root.getLeftNode() != null) {
            theInOrderTraversal(root.getLeftNode());
        }
        printNode(root);
        if (root.getRightNode() != null) {
            theInOrderTraversal(root.getRightNode());
        }
    }

    public void thePostOrderTraversal(Node root) {  //后序遍历
        if (root.getLeftNode() != null) {
            thePostOrderTraversal(root.getLeftNode());
        }
        if(root.getRightNode() != null) {
            thePostOrderTraversal(root.getRightNode());
        }
        printNode(root);
    }  

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        Node root = tree.init();
        System.out.println("先序遍历");
        tree.theFirstTraversal(root);
        System.out.println("");
        System.out.println("中序遍历");
        tree.theInOrderTraversal(root);
        System.out.println("");
        System.out.println("后序遍历");
        tree.thePostOrderTraversal(root);
        System.out.println("");
    }
}

3、借助队列实现层次遍历

//层次遍历
    public void theLeverTraversal(Node root) {
        if (root == null) {
            return;
        }
        //新建一个队列，LinkedList实现了Quene接口，可以直接当作队列来用
        LinkedList<Node> queue = new LinkedList<Node>();

        Node current;  //当前节点
        queue.offer(root);//根节点入队列

        while (!queue.isEmpty()) {
            current = queue.poll();  //取出队列的头节点
            System.out.print(current.val + " ");//输出队列的头节点的值
            if (current.left != null) {
                queue.offer(current.left);  //如果当前节点的左节点不为空，则左节点入队列
            }
            if (current.right != null) {
                queue.offer(current.right); //如果当前节点的右节点不为空，则右节点入队列
            }
        }
    }

4、堆栈方式实现前序、中序、后续遍历

public class BinaryTree1 {
     public Node init() {//注意必须逆序建立，先建立子节点，再逆序往上建立，因为非叶子结点会使用到下面的节点，而初始化是按顺序初始化的，不逆序建立会报错
            Node J = new Node(8, null, null);
            Node H = new Node(4, null, null);
            Node G = new Node(2, null, null);
            Node F = new Node(7, null, J);
            Node E = new Node(5, H, null);
            Node D = new Node(1, null, G);
            Node C = new Node(9, F, null);
            Node B = new Node(3, D, E);
            Node A = new Node(6, B, C);
            return A;   //返回根节点
        } 

    public void printNode(Node node){
        System.out.print(node.getData());
    }

    public void theFirstTraversal_Stack(Node root) {  //先序遍历
        Stack<Node> stack = new Stack<Node>();
        Node node = root;
        while (node != null || stack.size() > 0) {  //将所有左孩子压栈
            if (node != null) {   //压栈之前先访问
                printNode(node);
                stack.push(node);
                node = node.getLeftNode();
            } else {
                node = stack.pop();
                node = node.getRightNode();
            }
        }
    }  

    public void theInOrderTraversal_Stack(Node root) {  //中序遍历
        Stack<Node> stack = new Stack<Node>();
        Node node = root;
        while (node != null || stack.size() > 0) {
            if (node != null) {
                stack.push(node);   //直接压栈
                node = node.getLeftNode();
            } else {
                node = stack.pop(); //出栈并访问
                printNode(node);
                node = node.getRightNode();
            }
        }
    }  

    public void thePostOrderTraversal_Stack(Node root) {   //后序遍历
        Stack<Node> stack = new Stack<Node>();
        Stack<Node> output = new Stack<Node>();//构造一个中间栈来存储逆后序遍历的结果
        Node node = root;
        while (node != null || stack.size() > 0) {
            if (node != null) {
                output.push(node);
                stack.push(node);
                node = node.getRightNode();
            } else {
                node = stack.pop();
                node = node.getLeftNode();
            }
        }
        System.out.println(output.size());
        while (output.size() > 0) {

            printNode(output.pop());
        }
    }

    public static void main(String[] args) {
        BinaryTree1 tree = new BinaryTree1();
        Node root = tree.init();
        System.out.println("先序遍历");
        tree.theFirstTraversal_Stack(root);
        System.out.println("");
        System.out.println("中序遍历");
        tree.theInOrderTraversal_Stack(root);
        System.out.println("");
        System.out.println("后序遍历");
        tree.thePostOrderTraversal_Stack(root);
        System.out.println("");
    }
}

-------------------------------------------------------------------------------------------------------------------------

参考链接：

http://www.cnblogs.com/yaobolove/p/6213936.html

二叉树遍历（前序、中序、后序、层次、深度优先、广度优先遍历）：https://blog.csdn.net/yimingsilence/article/details/54783208