无线通信中FEC 编码原理及评价

转自：http://blog.csdn.net/wiznet2012/article/details/7492146

大家好，前面我们给大家介绍了无线通信中FEC编码原理（1）和（2），今天继续献上FEC编码原理及评价（3），关于不同FEC种类的评价，希望对大家有所帮助～

对于不同FEC的评价

这里我们介绍一些典型的FEC的应用并且做出一些解释和评价。我们根据不同的使用将这一部分分为两块。

1. 互联网中的FEC

这一部分，我们主要关注三个FEC的例子。

（1）Hamming码

Hamming码是由Hamming在1950年最初使用的，它是一种线性的纠错码，能自动监测出两个同时出现的比特错误并且纠正其中一个。这要比基础的奇偶校验码有效。

Hamming码不仅有很好的性能，而且它的编码和解码的电路都非常的简单并且易于实施。所以，它被广泛应用于小的电脑中。但是，Hamming码不能用于两个或两个以上错误比特的纠正。

Hamming码的例子

2）CRC码

CRC，是Cyclic Redundancy Check的缩写，是通信系统中最普遍也是最强大的错误检测码。它根据信息字段的长度而设计，而校验字段的长度可以随意选择。

利用CRC进行的错误检测的过程可以简单的描述为：发送端产生一段k比特的二进制码序列，之后根据特定的规则得出CRC码并附在原始码字后面。这个具有(k+r)比特的二进制码序列就可以被发送了。传输过程之后，接收端根据原始码与CRC码之间的规则检测到其中是否有错误。

CRC在互联网及其他领域的应用非常广泛，因为它具有很强的错误检测能力，低成本并且易于实现。CRC不能检测到错误的概率仅为0.0047%或更少。对于性能和成本来讲，CRC要比奇偶校验和算术检测要好的多。但是，CRC也很有可能会对于不同的信息产生相同的CRC码，尤其是当大量信息同时出现的时候。在这种情况下，CRC将会出现错误并且对于接收方重建原始信息增加了困难。例如，接收方必须要逐个比特进行检查来避免错误，这样会增加很多处理时间，所以，我们需要高性能的发送端和接收端。还有，CRC显然并不适合只具有低端CPU的设备。

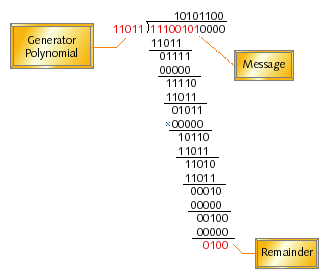
CRC码的计算

（3）BCH码

BCH码，最初由Bose、Ray-Chaudhuri and Hocquenghem提出，是Cyclic码的另一种重要分支。它具有纠正多个错误的能力。BCH码有严格的代数理论，是一种被最深入研究的编码方式。

BCH码的理论优势就是它的解码非常简便，通过被称为综合解码的代数方法来进行解码。这种方法只需要非常简单的电子硬件来完成这一任务，并不需要电脑。这样，解码的设备就可以做的很小并且需要很少的能源。所以，在BCH码的帮助下，我们可以利用低端的CPU和小型的设备高效的完成错误纠正，比如我们的手机。

无线通信中FEC 编码原理及评价（2）请参考：http://blog.csdn.net/wiznet2012/article/details/7468178