第四章 PCA降维
目录
1. PCA降维
PCA:主成分分析(Principe conponents Analysis)
2. 维度的概念
一般认为时间的一维,而空间的维度,众说纷纭。霍金认为空间是10维的。
3. 为什么要进行降维?
维度灾难:当维度超过一定值的时候,分类器效果呈现明显下降。
PCA旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。举一个简单的例子,在三维空间中有一系列数据点,这些点分布在一个过原点的平面上。如果我们用自然坐标系x,y,z三个轴来表示数据,就需要使用三个维度。而实际上,这些点只出现在一个二维平面上,如果我们通过坐标系旋转变换使得数据所在平面与x,y平面重合,那么我们就可以通过x,y两个维度表达原始数据,并且没有任何损失,这样就完成了数据的降维。而x,y两个轴所包含的信息就是我们要找到的主成分。
4. 目标
提取最有价值的信息(基于方差)
5. 降维后的数据的意义?
降维后物理意义变得模糊,但是不影响我们去后续做分类、预测等的结果。
6. PCA推导过程

7. 结论
- 我们要找最大的方差也就是协方差矩阵最大的特征值;
- 最佳投影方向就是最大特征值对应的特征向量
- 次佳投影方向位于最佳投影方向的正交空间中,是第二大特征值对应的特征向量
求解步骤:
- 对样本数据进行中心化处理
- 求协方差矩阵
- 对协方差矩阵进行特征值分解,将特征值从到小排列
- 取特征值前d大对应的特征向量w1, w2, ..., wd。通过映射关系将n维样本映射到d维空间。
降维后的信息占比定义为:
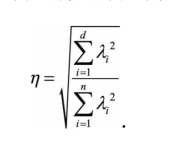
第四章 PCA降维的更多相关文章
- 第十四章:降维:奇异值分解SVD
- 机器学习实战基础(二十三):sklearn中的降维算法PCA和SVD(四) PCA与SVD 之 PCA中的SVD
PCA中的SVD 1 PCA中的SVD哪里来? 细心的小伙伴可能注意到了,svd_solver是奇异值分解器的意思,为什么PCA算法下面会有有关奇异值分解的参数?不是两种算法么?我们之前曾经提到过,P ...
- PRML读书会第四章 Linear Models for Classification(贝叶斯marginalization、Fisher线性判别、感知机、概率生成和判别模型、逻辑回归)
主讲人 planktonli planktonli(1027753147) 19:52:28 现在我们就开始讲第四章,第四章的内容是关于 线性分类模型,主要内容有四点:1) Fisher准则的分类,以 ...
- 《机器学习实战》学习笔记第十四章 —— 利用SVD简化数据
相关博客: 吴恩达机器学习笔记(八) —— 降维与主成分分析法(PCA) <机器学习实战>学习笔记第十三章 —— 利用PCA来简化数据 奇异值分解(SVD)原理与在降维中的应用 机器学习( ...
- R in action读书笔记(19)第十四章 主成分和因子分析
第十四章:主成分和因子分析 本章内容 主成分分析 探索性因子分析 其他潜变量模型 主成分分析(PCA)是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关变量称为主成分.探索性因 ...
- 【机器学习】--主成分分析PCA降维从初识到应用
一.前述 主成分分析(Principal Component Analysis,PCA), 是一种统计方法.通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分. ...
- Python机器学习笔记 使用scikit-learn工具进行PCA降维
之前总结过关于PCA的知识:深入学习主成分分析(PCA)算法原理.这里打算再写一篇笔记,总结一下如何使用scikit-learn工具来进行PCA降维. 在数据处理中,经常会遇到特征维度比样本数量多得多 ...
- PCA降维笔记
PCA降维笔记 一个非监督的机器学习算法 主要用于数据的降维 通过降维, 可以发现更便 于人类理解的特征 其他应用:可视化:去噪 PCA(Principal Component Analysis)是一 ...
- sklearn pca降维
PCA降维 一.原理 这篇文章总结的不错PCA的数学原理. PCA主成分分析是将原始数据以线性形式映射到维度互不相关的子空间.主要就是寻找方差最大的不相关维度.数据的最大方差给出了数据的最重要信息. ...
随机推荐
- jquery 特效
http://demo.howtoexe.com/instagram-gravity-gallery/index.html
- 实现一套山寨springMVC
重复造轮子没有意义,但是通过现已存在的轮子,模仿着思路去实现一套,还是比较cool的.花了三天,终于深夜搞定!收益都在代码里,我干了,您随意! 一.简单思路 简单介绍: 1.所有的请求交给TyDisp ...
- C++ dynamic_cast 的使用
C++中的dynamic_cast 执行运行时刻类型转换,起作用有点类似于Java当中的instance of reference:http://www.cnblogs.com/chio/archiv ...
- TortoiseGit disconnected no supported authentication
从远程服务器上获取到的工程,用Git没问题,而TortoiseGit报错: Disconnected: No supported authentication methods available(se ...
- linux之vim配置及使用示例
作者:tongqingliu 转载请注明出处:http://www.cnblogs.com/liutongqing/p/7056193.html linux之vim配置及使用示例 vi的三种模式: 一 ...
- 在Ubuntu上建立Arm Linux 开发环境
我使用的是友善2410的板子,以前都是用Fedora,现在家里的电脑被我转为Linux专用的了,装的是Ubuntu.但是嵌入式还是要玩的,在装载过程中也遇到一些小麻烦.在此记录一下,一来自己比较健忘, ...
- 利用irc服务器做物联网数据转发 c# winform程序
利用irc协议的优点: 免费,不用购买服务器就可以实现稳定公网转发数据 开源,irc的客户端和开源库众多,省去了自己造轮子的时间 历史悠久,互联网诞生伊始就有irc 缺点:安全性比较差 简单协议接收可 ...
- 第四章-shceme和数据类型优化
选择数据类型的原则: 1.更小通常更好.因为占用更少磁盘,内存和cpu缓存.但是要确保没有低估,因为进行alter时,是很耗时和头疼的操作.所以当无法确定数据类型的时候,选择不会超过范围的最小类型. ...
- Docker windows下安装并搭建Nodejs的webapp
一.关于Docker 什么是Docker?Docker 采用go语言编写,是一个开源的应用容器引擎.让开发者可以快速打包他们的应用以及依赖包到一个封装的可移植的容器Image中,然后发布到任何流行的机 ...
- U盘或者移动银盘退出时一直显示占用中问题解决--最粗暴解决方式
问题描述: ---------------------------弹出 USB 大容量存储设备 时出问题---------------------------Windows 无法停用“通用卷”设备,原 ...
