[学习笔记] Tarjan算法求强连通分量

今天，我们要探讨的就是——Tarjan算法。

Tarjan算法的主要作用便是求一张无向图中的强连通分量，并且用它缩点，把原本一个杂乱无章的有向图转化为一张DAG（有向无环图），以便解决之后的问题。

首先，我们在原图上跑一遍DFS，然后会发现三种边：

1、正常边：嗯，顾名思义就是连接祖先和儿子节点的边。

2、横叉边：连接到了已经弹出的节点的边（也能叫它小三边）。

3、返祖边：从儿子节点连到祖先的边。

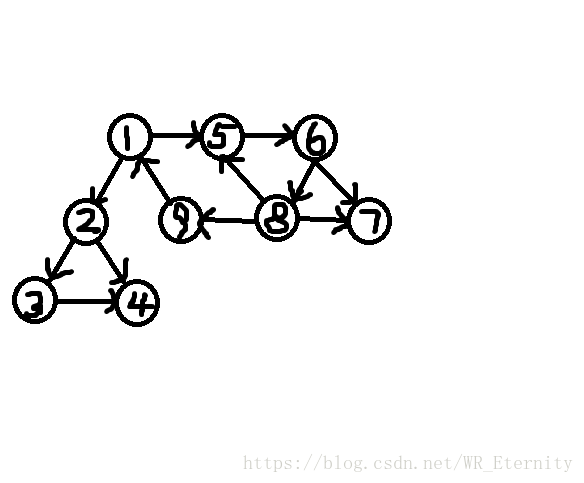
那么通过进一步的观察我们可以发现：返祖边可能产生强连通分量，而横叉边不能。（如下图所示）

DFS遍历之后即为：

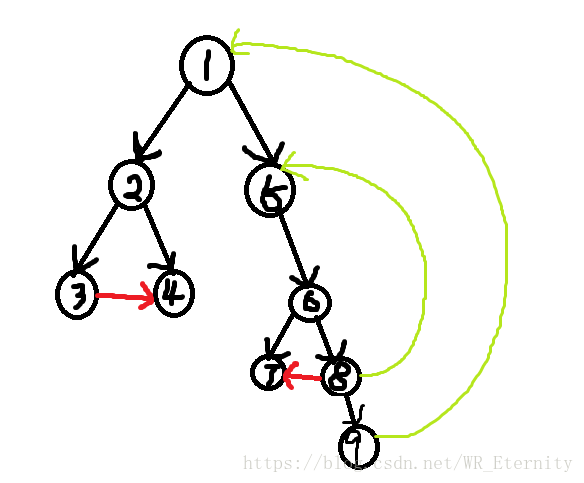
这时，我们发现上图出现了一种“大圈包小圈”的情况（{1-5-6-8-9}和{5-6-8-5}）那么我们应该如何处理才能做到当出现上图情况时只计算最大的那个强连通分量呢？

我们可以开两个数组：

dfn[i]：记录当遍历到节点i时是第几次dfs。

low[i]：记录以i为根的子树中能够连接到当前栈中最小的dfn值（也就是最上面的节点）。

然后每次取最小的low[i]就可以了。

Emmmmmmmmmmm，那就上代码吧。（Pascal党的福利哦）

var
  vis:array[1..100000]of boolean;
  stack,dfn,low,head,next,vet,blong,belong:array[1..100000]of longint;
  tot,time,top,x,y,i,n,m,point:longint;
function min(a,b:longint):longint;
begin
  if a<b then exit(a) else exit(b);
end;
procedure add(x,y:longint);
begin
  inc(tot);
  next[tot]:=head[x];
  vet[tot]:=y;
  head[x]:=tot;
end;
procedure tarjan(u:longint);
var
  i,v:longint;
begin
  inc(time);
  dfn[u]:=time; low[u]:=time;
  inc(top);
  stack[top]:=u; vis[u]:=true;
  i:=head[u];
  while i<>0 do
  begin
    v:=vet[i];
    if vis[v] then low[u]:=min(dfn[v],low[u])
      else if dfn[v]=0 then
      begin
        tarjan(v);
        low[u]:=min(low[v],low[u]);
      end;
    i:=next[i];
  end;
  if dfn[u]=low[u] then
  begin
    inc(point); belong[u]:=point;
    while stack[top]<>u do
    begin
      belong[stack[top]]:=point;
      vis[stack[top]]:=false;
      dec(top);
    end;
    vis[u]:=false; dec(top)
  end;
end;
procedure shrink_point;
var
  u,i,v:longint;
begin
  for u:=1 to n do
  begin
    i:=head[u];
    while i<>0 do
    begin
      v:=vet[i];
      if belong[i]<>belong[v] then add(belong[u],belong[v]);
      i:=next[i];
    end;
  end;
end;
begin
  read(n,m);
  point:=n;
  for i:=1 to m do
  begin
    read(x,y);
    add(x,y);
  end;
  for i:=1 to n do
    if dfn[i]=0 then tarjan(i);
  shrink_point;
end.