C#处理医学图像(二):基于Hessian矩阵的医学图像增强与窗宽窗位
根据本系列教程文章上一篇说到,在完成C++和Opencv对Hessian矩阵滤波算法的实现和封装后,
再由C#调用C++ 的DLL,(参考:C#处理医学图像(一):基于Hessian矩阵的血管肺纹理骨骼增强对比)
功能虽然已经实现,但在实际应用中要考虑到性能和耦合,本篇将介绍性能方面的注意点以及和其他功能的联动。
我们将Demo里面的功能集成到正式工程中:
1.新建一个新窗体,用来显示结果和调整滤波参数:
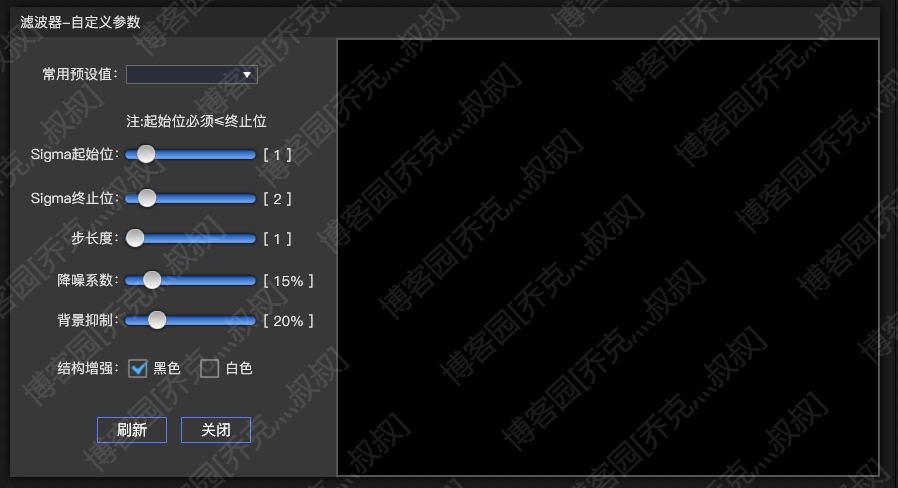
其中滑块控件选择工具箱中的Slider,定义好控件样式,变化事件选择PreviewMouseLeftButtonUp,不要用ValueChanged,
考虑到性能问题,因为是base64转码和解码,所以不推荐用ValueChanged,它的触发频率要高得多,
而在图像大小比较大的时候 base64加解密的效率显得不是很高,会造成主线程UI卡顿,所以只要响应鼠标抬起时计算图像即可。
<Slider x:Name="SgStart" Style="{StaticResource Slider_CustomStyle}" Width="132" Height="19" Value="1" IsMoveToPointEnabled="True" PreviewMouseLeftButtonUp="SgStart_PreviewMouseLeftButtonUp" />
2.显示计算结果:
在Slider控件鼠标抬起的事件中,先将目标单元格内WPF图像转为base64,发送给我们生成的C++接口,再将返回的base64转为WPF图像
[DllImport(@"opencv\ET.Functions.dll", EntryPoint = "GetFrangiBase64Code", CallingConvention = CallingConvention.Cdecl)]
public static extern IntPtr GetFrangiBase64Code(string base64code, int SIGMA_START, int SIGMA_END, int SIGMA_STEP, float BETA_ONE, float BETA_TWO, bool BLACKWHITE); /// <summary>
/// 获取滤波图像
/// </summary>
/// <param name="filterParm">滤波参数对象</param>
public void GetFilterImg(FilterParm filterParm)
{
try
{
string base64 = WriteableBitmapToBase64(Wbp);
IntPtr intPtr = GetFrangiBase64Code(base64,
filterParm.Start,
filterParm.End,
filterParm.Step,
filterParm.DenoiseNum,
filterParm.BgArgs,
filterParm.BgType); if (intPtr != IntPtr.Zero)
{
string filterCode = Marshal.PtrToStringAnsi(intPtr);
ImgBox.Source = Base64ToWriteableBitmap(filterCode);
}
}
catch (Exception e)
{
LogApi.WriteErrLog(e);
}
} /// <summary>
/// base64转WriteableBitmap
/// </summary>
/// <param name="base64">base64字符串</param>
public WriteableBitmap Base64ToWriteableBitmap(string base64)
{
byte[] streamBase = Convert.FromBase64String(base64);
BitmapImage bi = new BitmapImage();
bi.BeginInit();
bi.StreamSource = new MemoryStream(streamBase);
bi.EndInit();
WriteableBitmap wbp = new WriteableBitmap(bi);
return wbp;
} /// <summary>
/// WriteableBitmap转base64
/// </summary>
/// <param name="writeableBitmap">图像对象</param>
public string WriteableBitmapToBase64(WriteableBitmap writeableBitmap)
{
MemoryStream memStream = new MemoryStream();
JpegBitmapEncoder encoder = new JpegBitmapEncoder();
encoder.Frames.Add(BitmapFrame.Create(writeableBitmap));
encoder.Save(memStream);
byte[] bytes = memStream.ToArray();
string code = Convert.ToBase64String(bytes);
return code;
}
看效果:
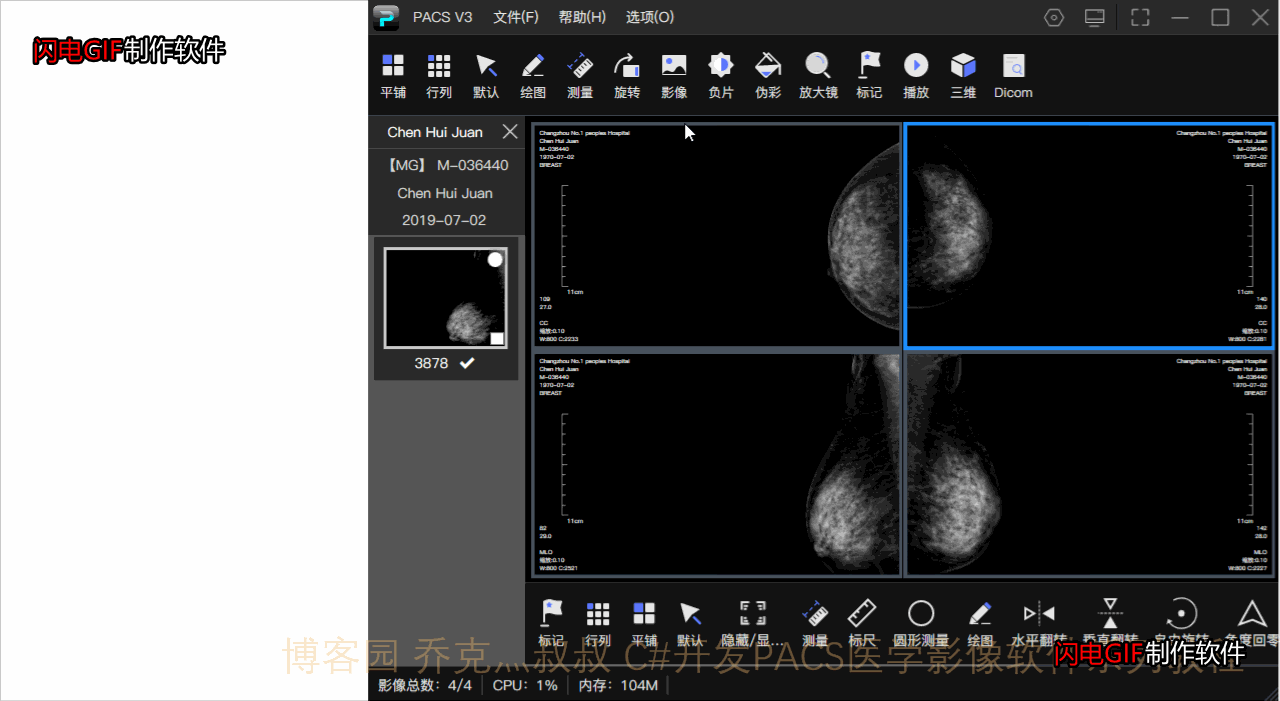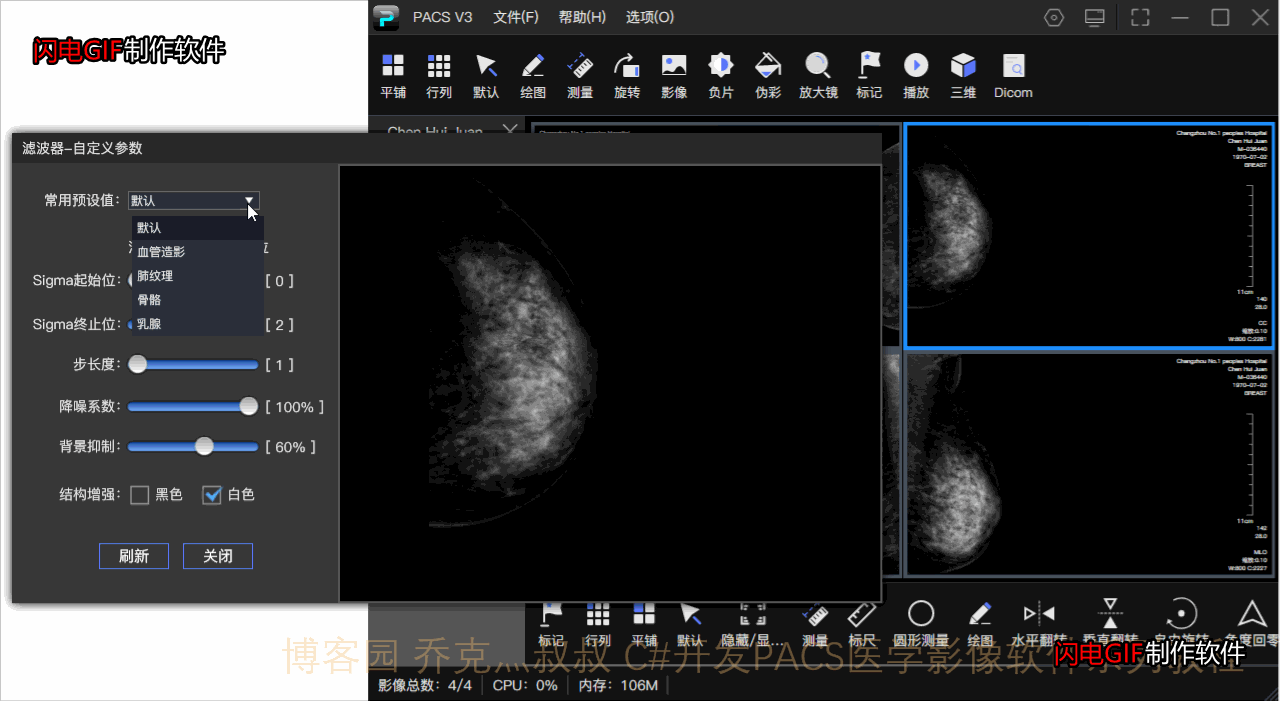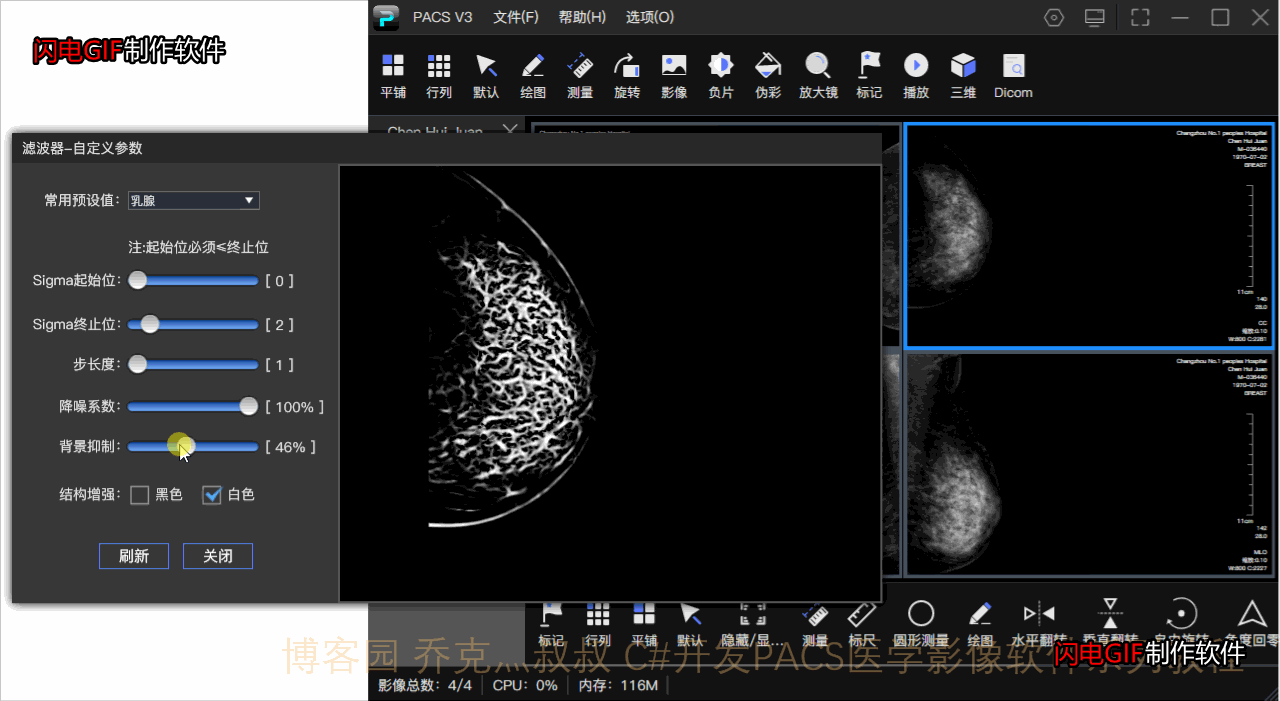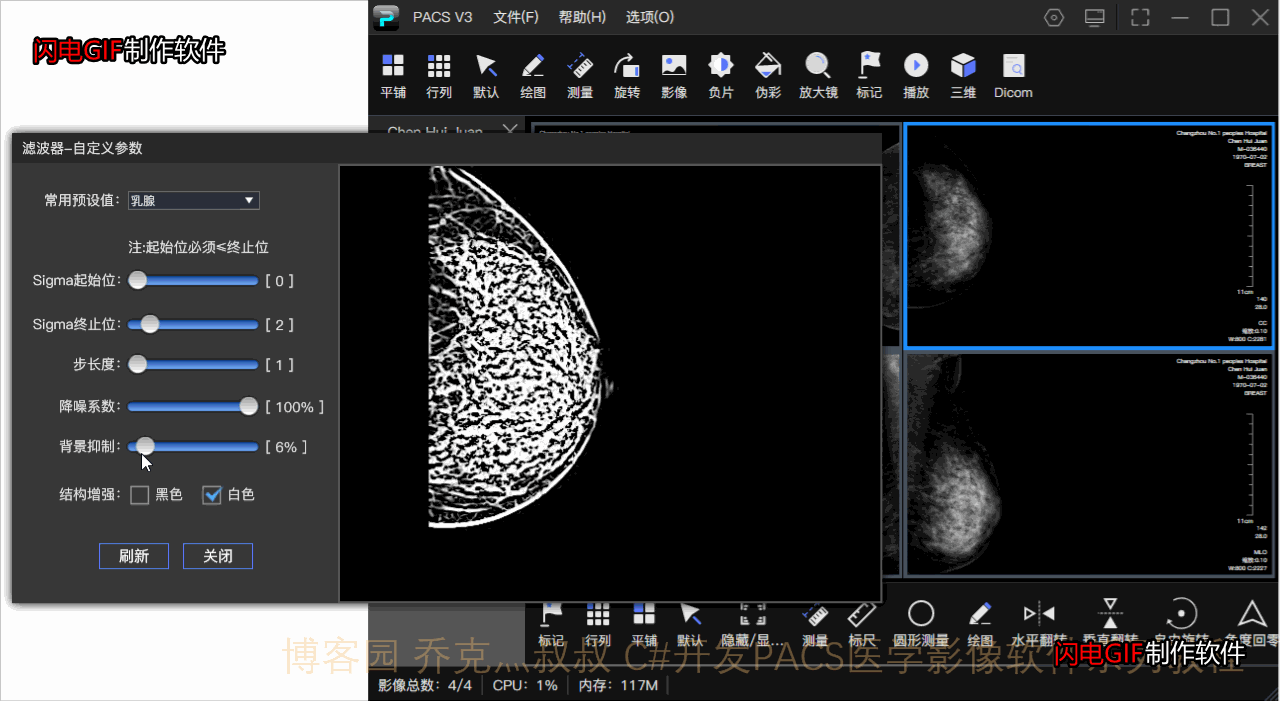
乳腺影像由原始dcm显示的絮状腺体在图像增强下变成丝状,对于乳腺中存在肿瘤或其他病症的显示更为明显,亦可自由调整参数达到自己想要的效果。
但有的情况下,增强效果却很差,显示的结果对于提取有价值的病灶信息几乎没有意义:
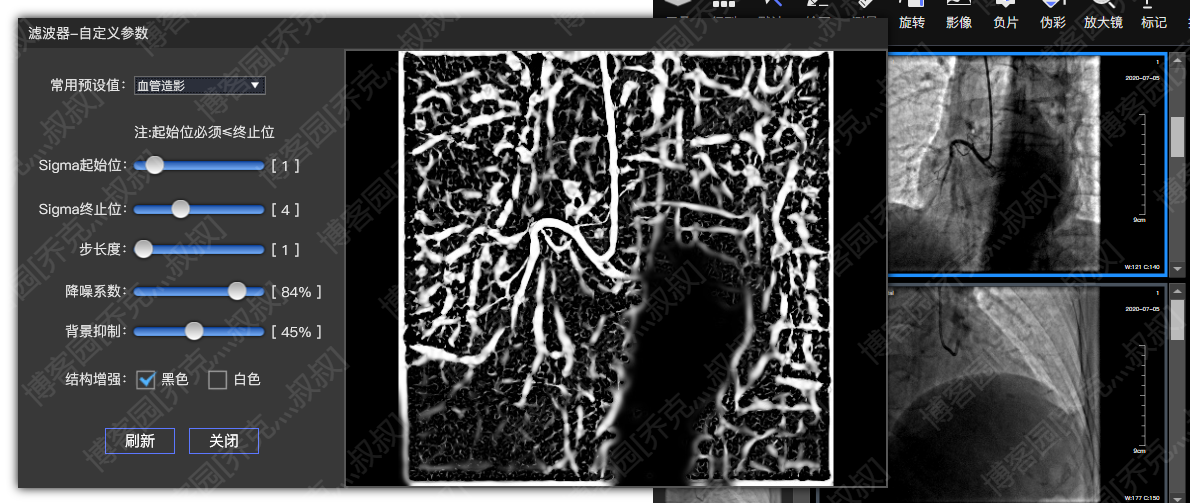
根据Hessian矩阵部分概念:

由原理中得知,求得特征值和特征向量反应出的变化上的各向异性,在二维图像中,
圆(点)具有各向同性,线性强度与各向异性程度成正比,
而在窗宽与窗位个概念中,血管的CT值为30左右,将窗宽窗位调整至增强前肉眼可见的差别,
最大程度降低二维图像上的无用信息,再利用海森矩阵加强线性结构,过滤圆(点)和降噪。
综上总结:先调整窗宽窗位,再图像增强和调整参数,使得效果最大化:
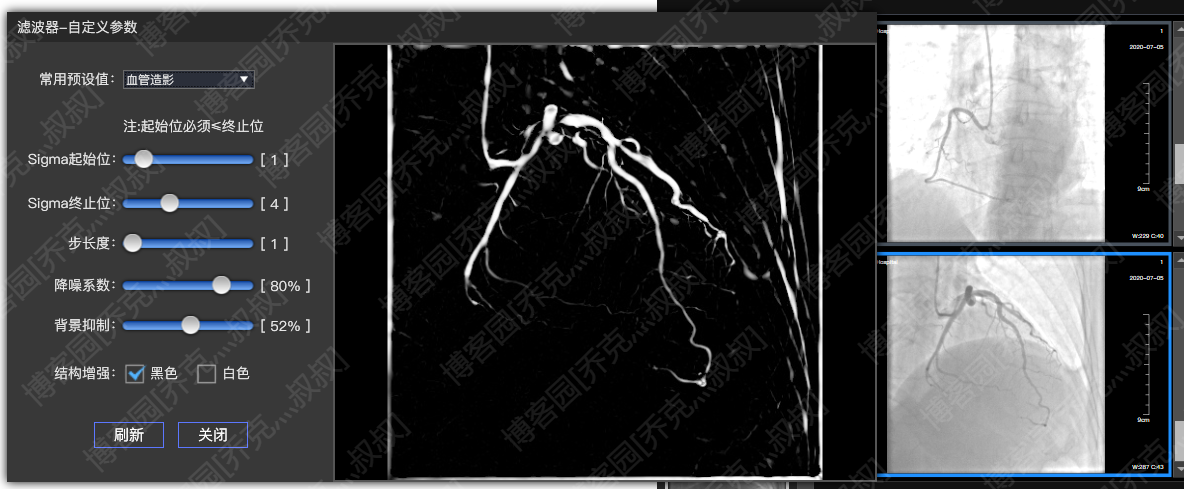
C#处理医学图像(二):基于Hessian矩阵的医学图像增强与窗宽窗位的更多相关文章
- C#处理医学图像(一):基于Hessian矩阵的血管肺纹理骨骼增强对比
在医院实际环境中,经常遇到有问题的患者,对于一些特殊的场景,比如骨折,肺结节,心脑血管问题 需要图像对比增强来更为清晰的显示病灶助于医生确诊,先看效果: 肺纹理增强: 肺结节增强: 血管对比增强: 骨 ...
- Hessian矩阵与多元函数极值
Hessian矩阵与多元函数极值 海塞矩阵(Hessian Matrix),又译作海森矩阵,是一个多元函数的二阶偏导数构成的方阵.虽然它是一个具有悠久历史的数学成果.可是在机器学习和图像处理(比如SI ...
- java学习-zxing生成二维码矩阵的简单例子
这个例子需要使用google的开源项目zxing的核心jar包 core-3.2.0.jar 可以百度搜索下载jar文件,也可使用maven添加依赖 <dependency> <gr ...
- Hessian矩阵与牛顿法
Hessian矩阵与牛顿法 牛顿法 主要有两方面的应用: 1. 求方程的根: 2. 求解最优化方法: 一. 为什么要用牛顿法求方程的根? 问题很多,牛顿法 是什么?目前还没有讲清楚,没关系,先直观理解 ...
- 【机器学习】梯度、Hessian矩阵、平面方程的法线以及函数导数的含义
想必单独论及" 梯度.Hessian矩阵.平面方程的法线以及函数导数"等四个基本概念的时候,绝大部分人都能够很容易地谈个一二三,基本没有问题. 其实在应用的时候,这几个概念经常被混 ...
- 梯度、Hessian矩阵、平面方程的法线以及函数导数的含义
本文转载自: Xianling Mao的专栏 =========================================================================== 想 ...
- Keil MDK STM32系列(二) 基于标准外设库SPL的STM32F401开发
Keil MDK STM32系列 Keil MDK STM32系列(一) 基于标准外设库SPL的STM32F103开发 Keil MDK STM32系列(二) 基于标准外设库SPL的STM32F401 ...
- CRL快速开发框架系列教程二(基于Lambda表达式查询)
本系列目录 CRL快速开发框架系列教程一(Code First数据表不需再关心) CRL快速开发框架系列教程二(基于Lambda表达式查询) CRL快速开发框架系列教程三(更新数据) CRL快速开发框 ...
- Jacobian矩阵和Hessian矩阵
1.Jacobian矩阵 在矩阵论中,Jacobian矩阵是一阶偏导矩阵,其行列式称为Jacobian行列式.假设 函数 $f:R^n \to R^m$, 输入是向量 $x \in R^n$ ,输出为 ...
随机推荐
- web移动端css reset
通用版css reset,pc端使用只需要修改html{font-size: 10px;}为html{font-size: 12px;} @charset "utf-8"; htm ...
- js onreadystatechange 和 onload的区别
IE的script 元素只支持onreadystatechange事件,不支持onload事件. FF的script 元素不支持onreadystatechange事件,只支持onload事件. 如果 ...
- NOI2008 志愿者招聘
文化课 + 竞赛双废物又来水题解了. 首先,对于题干中的人,很像网络流中的流量,但是他有一个每天人数的下限,我从网上借鉴(chaoxi)到了两种思路: 把下界限制转化为一条边的流量下界,这样就是最小费 ...
- Dwango Programming Contest 6th E 题解
题目大意 你有一条区间\([0, X)\),并且有一个数组\(L_1, ..., L_n\).对于任意\(1 \leq i \leq n\),你可以指定一个非负整数\(0 \leq j_i \leq ...
- Docker安装rocketmq踩坑指南
Docker 网络 Docker容器运行的时候有host.bridge.none三种网络可供配置. 默认是bridge,即桥接网络,以桥接模式连接到宿主机:host是宿主网络,即与宿主机共用网络:no ...
- 使用Swiper快速实现3D效果轮播
最近经常接到轮播图3D效果的需求, 特在此记录一下以备之后使用. 具体实现效果如下: 在这里介绍两种使用方式, 一种原生的html+php后端渲染, 一种是使用vue. 原生实现 引入 首先我们介绍原 ...
- mysql 8.0忘记root密码
1.修改参数文件添加以下内容 skip-grant-tables 2.关闭数据库 [root@node01 ~]# /etc/init.d/mysqld8 stop Shutting down MyS ...
- IOS UITableView 加载未知宽高图片的解决方案
在开发中遇到了UITableView列表 UITableViewCell装载图片但不知Image的宽高 问题. 在解决该问题的时候,首先想到的是异步加载图片 采用第三方框架SDWebImage 实现对 ...
- Spark内核-内存管理
Spark 集群会启动 Driver 和 Executor 两种 JVM 进程 我们只关注Executor的内存. 分为堆内内存和堆外内存 内存分为 存储内存 : 存储数据用的. 执行内存: 执行sh ...
- Linux音频编程--使用ALSA库播放wav文件
在UBUNTU系统上使用alsa库完成了对外播放的wav文件的案例. 案例代码: /** *test.c * *注意:这个例子在Ubuntu 12.04.1环境下编译运行成功. * */ #inclu ...
