机器学习:Python中如何使用支持向量机(SVM)算法
(简单介绍一下支持向量机,详细介绍尤其是算法过程可以查阅其他资)
在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别、分类(异常值检测)以及回归分析。
其具有以下特征:
(1)SVM可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法都采用一种基于贪心学习的策略来搜索假设空间,这种方法一般只能获得局部最优解。
(2) SVM通过最大化决策边界的边缘来实现控制模型的能力。尽管如此,用户必须提供其他参数,如使用核函数类型和引入松弛变量等。
from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt #准备训练样本
x=[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49]]
y=[1,1,-1,-1,1,-1,-1,1] ##开始训练
clf=svm.SVC() ##默认参数:kernel='rbf'
clf.fit(x,y) #print("预测...")
#res=clf.predict([[2,2]]) ##两个方括号表面传入的参数是矩阵而不是list ##根据训练出的模型绘制样本点
for i in x:
res=clf.predict(np.array(i).reshape(1, -1))
if res > 0:
plt.scatter(i[0],i[1],c='r',marker='*')
else :
plt.scatter(i[0],i[1],c='g',marker='*') ##生成随机实验数据(15行2列)
rdm_arr=np.random.randint(1, 15, size=(15,2))
##回执实验数据点
for i in rdm_arr:
res=clf.predict(np.array(i).reshape(1, -1))
if res > 0:
plt.scatter(i[0],i[1],c='r',marker='.')
else :
plt.scatter(i[0],i[1],c='g',marker='.')
##显示绘图结果
plt.show()
结果如下图:
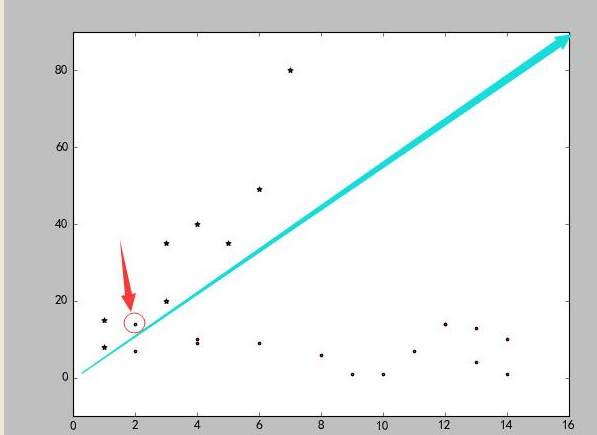
从图上可以看出,数据明显被蓝色分割线分成了两类。但是红色箭头标示的点例外,所以这也起到了检测异常值的作用。
2.在上面的代码中提到了kernel='rbf',这个参数是SVM的核心:核函数
重新整理后的代码如下:
from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt ##设置子图数量
fig, axes = plt.subplots(nrows=2, ncols=2,figsize=(7,7))
ax0, ax1, ax2, ax3 = axes.flatten() #准备训练样本
x=[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49]]
y=[1,1,-1,-1,1,-1,-1,1]
'''
说明1:
核函数(这里简单介绍了sklearn中svm的四个核函数,还有precomputed及自定义的) LinearSVC:主要用于线性可分的情形。参数少,速度快,对于一般数据,分类效果已经很理想
RBF:主要用于线性不可分的情形。参数多,分类结果非常依赖于参数
polynomial:多项式函数,degree 表示多项式的程度-----支持非线性分类
Sigmoid:在生物学中常见的S型的函数,也称为S型生长曲线 说明2:根据设置的参数不同,得出的分类结果及显示结果也会不同 '''
##设置子图的标题
titles = ['LinearSVC (linear kernel)',
'SVC with polynomial (degree 3) kernel',
'SVC with RBF kernel', ##这个是默认的
'SVC with Sigmoid kernel']
##生成随机试验数据(15行2列)
rdm_arr=np.random.randint(1, 15, size=(15,2)) def drawPoint(ax,clf,tn):
##绘制样本点
for i in x:
ax.set_title(titles[tn])
res=clf.predict(np.array(i).reshape(1, -1))
if res > 0:
ax.scatter(i[0],i[1],c='r',marker='*')
else :
ax.scatter(i[0],i[1],c='g',marker='*')
##绘制实验点
for i in rdm_arr:
res=clf.predict(np.array(i).reshape(1, -1))
if res > 0:
ax.scatter(i[0],i[1],c='r',marker='.')
else :
ax.scatter(i[0],i[1],c='g',marker='.') if __name__=="__main__":
##选择核函数
for n in range(0,4):
if n==0:
clf = svm.SVC(kernel='linear').fit(x, y)
drawPoint(ax0,clf,0)
elif n==1:
clf = svm.SVC(kernel='poly', degree=3).fit(x, y)
drawPoint(ax1,clf,1)
elif n==2:
clf= svm.SVC(kernel='rbf').fit(x, y)
drawPoint(ax2,clf,2)
else :
clf= svm.SVC(kernel='sigmoid').fit(x, y)
drawPoint(ax3,clf,3)
plt.show()
结果如图:
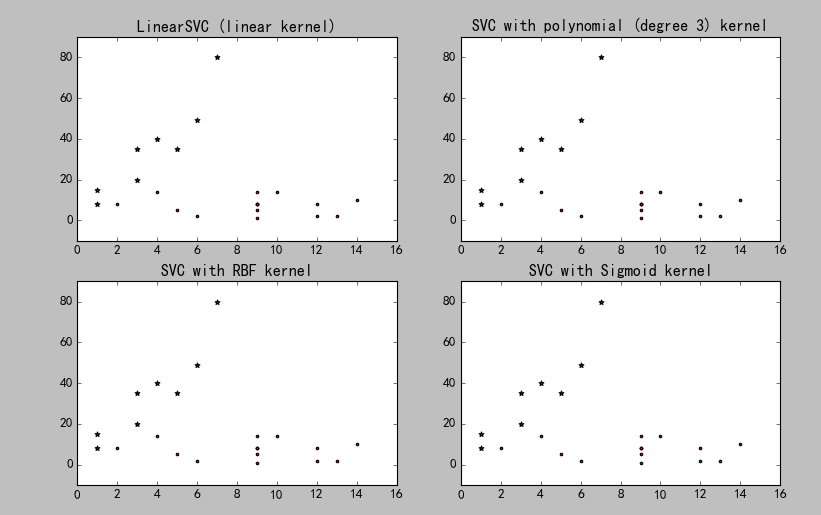
由于样本数据的关系,四个核函数得出的结果一致。在实际操作中,应该选择效果最好的核函数分析。
3.在svm模块中还有一个较为简单的线性分类函数:LinearSVC(),其不支持kernel参数,因为设计思想就是线性分类。如果确定数据
可以进行线性划分,可以选择此函数。跟kernel='linear'用法对比如下:
from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt ##设置子图数量
fig, axes = plt.subplots(nrows=1, ncols=2,figsize=(7,7))
ax0, ax1 = axes.flatten() #准备训练样本
x=[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49]]
y=[1,1,-1,-1,1,-1,-1,1] ##设置子图的标题
titles = ['SVC (linear kernel)',
'LinearSVC'] ##生成随机试验数据(15行2列)
rdm_arr=np.random.randint(1, 15, size=(15,2)) ##画图函数
def drawPoint(ax,clf,tn):
##绘制样本点
for i in x:
ax.set_title(titles[tn])
res=clf.predict(np.array(i).reshape(1, -1))
if res > 0:
ax.scatter(i[0],i[1],c='r',marker='*')
else :
ax.scatter(i[0],i[1],c='g',marker='*')
##绘制实验点
for i in rdm_arr:
res=clf.predict(np.array(i).reshape(1, -1))
if res > 0:
ax.scatter(i[0],i[1],c='r',marker='.')
else :
ax.scatter(i[0],i[1],c='g',marker='.') if __name__=="__main__":
##选择核函数
for n in range(0,2):
if n==0:
clf = svm.SVC(kernel='linear').fit(x, y)
drawPoint(ax0,clf,0)
else :
clf= svm.LinearSVC().fit(x, y)
drawPoint(ax1,clf,1)
plt.show()
结果如图所示:
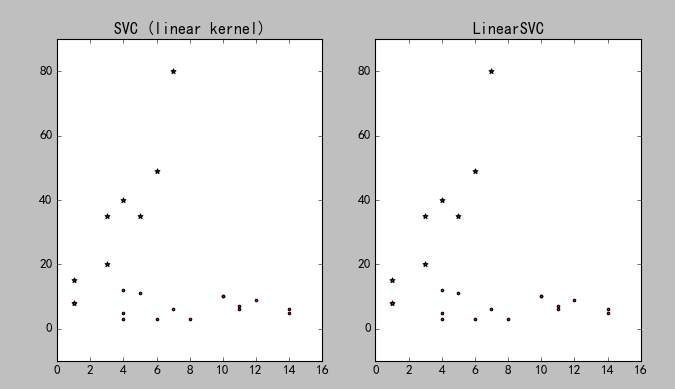
机器学习:Python中如何使用支持向量机(SVM)算法的更多相关文章
- 一步步教你轻松学支持向量机SVM算法之案例篇2
一步步教你轻松学支持向量机SVM算法之案例篇2 (白宁超 2018年10月22日10:09:07) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- 一步步教你轻松学支持向量机SVM算法之理论篇1
一步步教你轻松学支持向量机SVM算法之理论篇1 (白宁超 2018年10月22日10:03:35) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- 4、2支持向量机SVM算法实践
支持向量机SVM算法实践 利用Python构建一个完整的SVM分类器,包含SVM分类器的训练和利用SVM分类器对未知数据的分类, 一.训练SVM模型 首先构建SVM模型相关的类 class SVM: ...
- Spark机器学习系列之13: 支持向量机SVM
Spark 优缺点分析 以下翻译自Scikit. The advantages of support vector machines are: (1)Effective in high dimensi ...
- spark机器学习从0到1支持向量机SVM(五)
分类 分类旨在将项目分为不同类别. 最常见的分类类型是二元分类,其中有两类,通常分别为正数和负数. 如果有两个以上的类别,则称为多类分类. spark.mllib支持两种线性分类方法:线性支持 ...
- 吴恩达机器学习笔记(六) —— 支持向量机SVM
主要内容: 一.损失函数 二.决策边界 三.Kernel 四.使用SVM (有关SVM数学解释:机器学习笔记(八)震惊!支持向量机(SVM)居然是这种机) 一.损失函数 二.决策边界 对于: 当C非常 ...
- 机器学习(四):通俗理解支持向量机SVM及代码实践
上一篇文章我们介绍了使用逻辑回归来处理分类问题,本文我们讲一个更强大的分类模型.本文依旧侧重代码实践,你会发现我们解决问题的手段越来越丰富,问题处理起来越来越简单. 支持向量机(Support Vec ...
- python中的MRO和C3算法
一. 经典类和新式类 1.python多继承 在继承关系中,python子类自动用友父类中除了私有属性外的其他所有内容.python支持多继承.一个类可以拥有多个父类 2.python2和python ...
- 机器学习-Python中训练模型的保存和再使用
模型保存 BP:model.save(save_dir) SVM: from sklearn.externals import joblib joblib.dump(clf, save_dir) 模型 ...
随机推荐
- node.js 学习随笔
一,cnmp的操作: 1,cnmp info jquery查询jquery的版本: 2,cnmp install jquery@1.11.1:安装: 3,cnmp list查询所有下载的内容: 4,c ...
- 获取div滚动条的宽度
获取滚动条的宽度: function getScrollWidth() { var noScroll, scroll, oDiv = document.createElement('div'); oD ...
- (Jquery)避免数据相加小数点后产生多位数和计算精度损失
/** * 加法运算,避免数据相加小数点后产生多位数和计算精度损失. * * @param num1加数1 | num2加数2 */ function numAdd(num1, num2) { var ...
- 深入了解Unity中LineRenderer与TrailRenderer
LineRender和TrailRender是两个好东西,很多Unity拖尾特效都会使用到它们.一些简单的介绍可以参见官方的API文档.在这里探讨一下它们具体的渲染方式,而后给出一些Shader以便更 ...
- Windows Form线程同步
.Net多线程开发中,经常需要启动工作线程Worker thread处理某些事情,而工作线程中又需要更新主线程UI thread的界面状态.我们只能在主线程中操作界面控件,否则.Net会抛出异常. 那 ...
- Unity3d的序列帧动画
马上这星期就要过去了,为了完成每星期写一篇博客的目标,熬夜也要写完. 最近项目中用到了很多序列帧动画,之前看教程也接触过序列帧动画,但当时没用到,就没仔细研究,这次就借着这个机会好好总结一下序列帧动画 ...
- 漂亮的代码2:遍历文件夹目录,使用promise
看到一个问题: 找到文件夹下所有文件: 自己写了一个: function walk(dir, ext, callback) { ext = ext.charAt(0) === "." ...
- 每天一个linux命令(32)--/etc/group文件详解
Linux /etc/group 文件与 /etc/passwd 和/etc/shadow 文件都是有关于系统管理员对用户和用户组管理时相关的文件.Linux /etc/group 文件是有关于系统管 ...
- 【Zookeeper】源码分析之Leader选举(二)
一.前言 前面学习了Leader选举的总体框架,接着来学习Zookeeper中默认的选举策略,FastLeaderElection. 二.FastLeaderElection源码分析 2.1 类的继承 ...
- Java I/O之NIO概念理解
JDK1.4的java.nio.*包引入了新的Java I/O新类库,其目的在于提高速度.实际上,旧的I/O包已经使用nio重新实现过,以便充分利用这种速度提高,因此即使我们不显式地用nio编码,也能 ...
