【js数据结构】可逐次添加叶子的二叉树(非最优二叉树)
最近小菜鸟西瓜莹看到了一道面试题:
给定二叉树,按层打印。例如1的子节点是2、3, 2的子节点是3、4, 5的子节点是6,7.
需要建立如图二叉树:
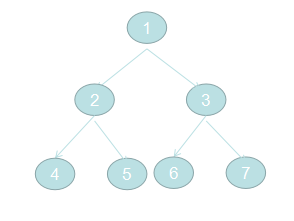
但是西瓜莹找到的相关代码都是用js构建最优二叉树,假如,依次向二叉树中添加4,2,6,1,3,5,7最优二叉树如图:

比根节点小的节点总是放在根节点的左节点上,比根节点大的节点总是放在根节点的右节点上。
假如想依次向二叉树添加1,2,3,4,5,6,7 二叉树又是如何呢?
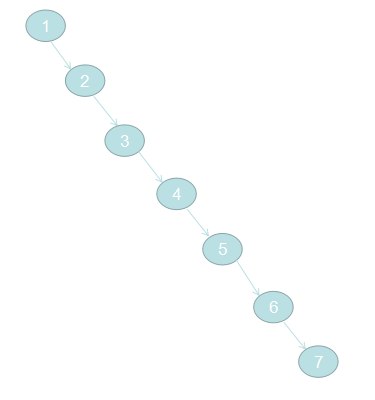
后一个数据总是比前一个数据大,那么就会一直在根节点的右节点上。
构建最优二叉树的核心就是添加节点的函数,记录当前节点,如果新数据比当前节点小,则让新数据成为左节点。否则成为右节点。
代码如下:
function addNode(ele){
var n = new Node(ele, null, null);
var Que = [];
if(this.root == null)
{
this.root = n;
}
else {
var curr = this.root;
var parent;
while(true)
{
parent = curr;
if(ele<curr.element)
{
curr = curr.left;
if( curr == null)
{
parent.left = n;
break;
}
}
else{
curr = curr.right;
if(curr == null)
{
parent.right = n;
break;
}
}
}
}
}
}
可是目的并不是创建最优二叉树,而是创建1,2,3,4,5,6,7这样的二叉树,那么如何实现呢?
思路:用一个队列来存储节点,将根节点放入队列中,如果根节点既有左节点又有右节点,将左右节点放入队列,如果没有左节点,将新数据放在左节点上,如果没有右节点,就将新数据放在右节点上。
代码:
function addNode(ele){
var n = new Node(ele, null, null);
var Que = [];
if(this.root == null)
{
this.root = n;
}
else {
var curr = this.root;
Que.push(curr);
}
while(Que.length>0)
{
curr = Que.shift();
if(curr.left != null && curr.right != null)
{
Que.push(curr.left);
Que.push(curr.right);
}
else if(curr.left == null )
{
curr.left = n;
break;
}
else if(curr.right == null)
{
curr.right = n;
break;
}
}
}
二叉树的遍历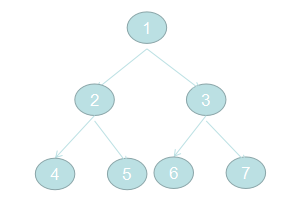
层次遍历也采用队列思想:
function showLevel(node)
{
var queue = [];
var curr;
if(this.root != null)
{
queue.push(this.root)
}
while(queue.length>0)
{
curr = queue.shift();
console.info(curr.element)
if(curr.left != null && curr.right != null)
{
queue.push(curr.left);
queue.push(curr.right);
}
else if(curr.left == null )
{
continue;
}
else if(curr.right == null)
{
queue.push(curr.left);
continue;
}
}
}
执行结果:

先序遍历:
function showTree(node){
if(!(node == null))
{
node.show();
showTree(node.left);
showTree(node.right);
}
}
运行结果:

完整代码:
function Node(ele, left, right){
this.element = ele;
this.left = left;
this.right = right;
this.show = show;
}
function show(){
console.log(this.element);
}
function BinaryTree(){
this.root = null;
this.addNode = addNode;
this.showTree = showTree;
this.showLevel = showLevel;
}
function addNode(ele){
var n = new Node(ele, null, null);
var Que = [];
if(this.root == null)
{
this.root = n;
}
else {
var curr = this.root;
Que.push(curr);
}
while(Que.length>0)
{
curr = Que.shift();
if(curr.left != null && curr.right != null)
{
Que.push(curr.left);
Que.push(curr.right);
}
else if(curr.left == null )
{
curr.left = n;
break;
}
else if(curr.right == null)
{
curr.right = n;
break;
}
}
}
function showTree(node){
if(!(node == null))
{
node.show();
showTree(node.left);
showTree(node.right);
}
}
function showLevel(node)
{
var queue = [];
var curr;
if(this.root != null)
{
queue.push(this.root)
}
while(queue.length>0)
{
curr = queue.shift();
console.info(curr.element)
if(curr.left != null && curr.right != null)
{
queue.push(curr.left);
queue.push(curr.right);
}
else if(curr.left == null )
{
continue;
}
else if(curr.right == null)
{
queue.push(curr.left);
continue;
}
}
}
var Tree = new BinaryTree();
Tree.addNode(1)
Tree.addNode(2)
Tree.addNode(3)
Tree.addNode(4)
Tree.addNode(5)
Tree.addNode(6)
Tree.addNode(7)
showTree(Tree.root)
Tree.showLevel(Tree.root)
这样,我们就构建了一个二叉树:
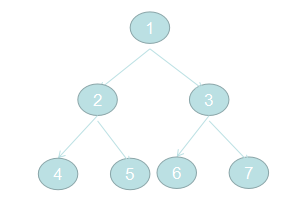
【js数据结构】可逐次添加叶子的二叉树(非最优二叉树)的更多相关文章
- Data Structure 之 最优二叉树
给定n个权值作为n的叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree).哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近. ...
- 树和二叉树->最优二叉树
文字描述 结点的路径长度 从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径,路径上的分支数目称作路径长度. 树的路径长度 从树根到每一个结点的路径长度之和叫树的路径长度. 结点的带权路径长 ...
- 数据结构(3) 第三天 栈的应用:就近匹配/中缀表达式转后缀表达式 、树/二叉树的概念、二叉树的递归与非递归遍历(DLR LDR LRD)、递归求叶子节点数目/二叉树高度/二叉树拷贝和释放
01 上节课回顾 受限的线性表 栈和队列的链式存储其实就是链表 但是不能任意操作 所以叫受限的线性表 02 栈的应用_就近匹配 案例1就近匹配: #include <stdio.h> in ...
- JS数据结构第五篇 --- 二叉树和二叉查找树
一.二叉树的基本概念 从逻辑结构角度来看,前面说的链表.栈.队列都是线性结构:而今天要了解的“二叉树”属于树形结构. 1.1 多叉树的基本概念,以上图中“多叉树”为例说明 节点:多叉树中的每一个点都叫 ...
- 数据结构之Huffman树与最优二叉树
最近在翻炒一些关于树的知识,发现一个比较有意思的二叉树,huffman树,对应到离散数学中的一种名为最优二叉树的路径结构,而Huffman的主要作用,最终可以归结到一种名为huffman编码的编码方式 ...
- JS数据结构第三篇---双向链表和循环链表之约瑟夫问题
一.双向链表 在上文<JS数据结构第二篇---链表>中描述的是单向链表.单向链表是指每个节点都存有指向下一个节点的地址,双向链表则是在单向链表的基础上,给每个节点增加一个指向上一个节点的地 ...
- JS数据结构之 Map
JS数据结构之 Map Map介绍 Map(映射)是ES6引入的一种数据结构.这是一种存储键值对列表很方便的方法,类似于其他编程语言的哈希表. HashMap(哈希表),也叫做散列表.是根据关键码值 ...
- js对select动态添加和删除OPTION
<select id="ddlResourceType" onchange="getvalue(this)"> </select> 动态 ...
- JS对select动态添加options操作[IE&FireFox兼容]
<select id="ddlResourceType" onchange="getvalue(this)"> </select> 动态 ...
随机推荐
- Linux配置JDK
在etc/profile文件下添加 export JAVA_HOME=/root/Desktop/jdk1.7.0_79 export CLASSPATH=/root/Desktop/jdk1.7.0 ...
- BOM元素之location对象
location对象提供了与当前窗口中加载的文档有关的信息,还提供了一些导航功能,它既是window对象的属性,也是document对象的属性:换句话说,window.location和documen ...
- 【Zookeeper】源码分析之网络通信(二)
一.前言 前面介绍了ServerCnxn,下面开始学习NIOServerCnxn. 二.NIOServerCnxn源码分析 2.1 类的继承关系 public class NIOServerCnxn ...
- Jquery之JSON的用法
今天讲了Jquery里面JSON的用法,下面是今天讲课给的例子: <!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01//EN" &quo ...
- ASP渲染下拉框使时间依次减少
<% x=year(now()) y=year(now())-1 Do While y>2002%><li><a href="#201 ...
- 在.NET项目中使用PostSharp,使用CacheManager实现多种缓存框架的处理
在前面几篇随笔中,介绍了PostSharp的使用,以及整合MemoryCache,<在.NET项目中使用PostSharp,实现AOP面向切面编程处理>.<在.NET项目中使用Pos ...
- Linux命令语句秘籍
系统管理命令 stat 显示指定文件的详细信息,比ls更详细 who 显示在线登陆用户 whoami 显示当前操作用户 host ...
- jmeter的http cookies管理器使用
关于Cookie不过多介绍,测试UI的小伙伴们应该对此有深深的爱和恨~ 本文介绍如何:1.获取Cookie.2.保存Cookie 3.引用Cookie 最终达到Cookie类似无法失效的目的~ Coo ...
- Django REST framework使用ViewSets的自定义路由实现过程
在Django中使用基于类的视图(ClassView),类中所定义的方法名称与Http的请求方法相对应,才能基于路由将请求分发(dispatch)到ClassView中的方法进行处理,而Django ...
- NOI全国赛(1998)——围巾裁剪
裁缝有一块非常珍贵的丝绸围巾.可惜的是,围巾的某些部分已经被蛀虫给咬坏了.裁缝当然不愿意就这么把围巾给丢了,于是,他想把围巾给裁成两块小围巾送给他的两个女儿.自然,两块小围巾的面积之和越大越好. 这 ...
