HDU-1828-Picture(线段树)

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the
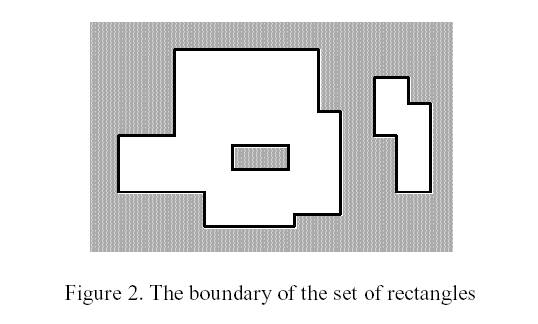
boundary of the union of all rectangles is called the perimeter.



Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.









The corresponding boundary is the whole set of line segments drawn in Figure 2.








The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex
of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.




0 <= number of rectangles < 5000

All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.



Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

 

Sample Output

228

 

Source

IOI 1998

思路：求纵向边要维护重叠次数大于0的纵向长度。用上一次的node[1].m减去当前的node[1].m的绝对值。求横向边要维护每一次更新之后须要加上去的边数。

#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;

struct L{
int val;//1 左边。-1 右边
int x,y1,y2;
}l[10000];

struct N{
int l,r,n,m;//n记录节点相应的有效横向边数量，m记录纵向长度
int cnt;//重叠情况
bool lc,rc;
}node[40000];

int tempy[10000];

bool cmp(struct L a,struct L b)
{
    if(a.x==b.x) return a.val>b.val;

    return a.x<b.x;
}

void build(int idx,int s,int e)
{
    node[idx].cnt=0;
    node[idx].m=0;
    node[idx].lc=node[idx].rc=0;
    node[idx].l=tempy[s-1];
    node[idx].r=tempy[e-1];

    if(s+1!=e)
    {
        int mid=(s+e)>>1;

        build(idx<<1,s,mid);
        build(idx<<1|1,mid,e);
    }
}

void len(int idx,int s,int e)
{
    if(node[idx].cnt>0)
    {
        node[idx].m=node[idx].r-node[idx].l;
        node[idx].n=2;//相应两条边
        node[idx].lc=node[idx].rc=1;
    }
    else
    {
        if(s+1!=e)
        {
            int mid=(s+e)>>1;

            node[idx].m=node[idx<<1].m+node[idx<<1|1].m;
            node[idx].n=node[idx<<1].n+node[idx<<1|1].n;
            node[idx].lc=node[idx<<1].lc;
            node[idx].rc=node[idx<<1|1].rc;
            if(node[idx<<1].rc && node[idx<<1|1].lc) node[idx].n-=2;//假设左右儿子是连着的。就要减去多计算的两条边
        }
        else
        {
            node[idx].m=0;
            node[idx].n=0;
            node[idx].lc=node[idx].rc=0;
        }
    }
}

void update(int idx,int s,int e,struct L line)
{
    if(node[idx].l==line.y1 && node[idx].r==line.y2)
    {
        node[idx].cnt+=line.val;
        len(idx,s,e);
        return;
    }

    if(s+1!=e)
    {
        int mid=(s+e)>>1;

        if(line.y2<=node[idx<<1].r) update(idx<<1,s,mid,line);
        else if(line.y1>=node[idx<<1|1].l) update(idx<<1|1,mid,e,line);
        else
        {
            int temp=line.y2;

            line.y2=node[idx<<1].r;
            update(idx<<1,s,mid,line);
            line.y2=temp;

            line.y1=node[idx<<1|1].l;
            update(idx<<1|1,mid,e,line);
        }

    }

    len(idx,s,e);
}

int main()
{
    int T,n,i,t;
    int x1,x2,y1,y2;

    while(~scanf("%d",&n))
    {
        for(i=0;i<n;i++)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);

            tempy[i*2]=y1;
            tempy[i*2+1]=y2;

            l[i*2].val=1;
            l[i*2].x=x1;
            l[i*2].y1=y1;
            l[i*2].y2=y2;

            l[i*2+1].val=-1;
            l[i*2+1].x=x2;
            l[i*2+1].y1=y1;
            l[i*2+1].y2=y2;
        }

        sort(tempy,tempy+n*2);
        sort(l,l+n*2,cmp);

        t=unique(tempy,tempy+n*2)-tempy;//去重

        build(1,1,t);

        int ans=0,last=0;

        for(i=0;i<n*2;i++)
        {
            if(i) ans+=node[1].n*(l[i].x-l[i-1].x);

            update(1,1,t,l[i]);

            ans+=abs(node[1].m-last);
            last=node[1].m;
        }

        printf("%d\n",ans);
    }
}