[国家集训队]最长双回文串 manacher

～～～题面～～～

题解：

首先有一个直观的想法，如果我们可以求出对于位置i的最长后缀回文串和最长前缀回文串，那么我们枚举分界点然后合并前缀和后缀不就可以得到答案了么？

所以我们的目标就是求出这两个数列，

我们令f[i] 表示以i为结尾的最长回文后缀的长度，g[i]表示以i为开头的最长回文后缀的长度。

由于要找回文串，因此我们先想到manacher。

然后我们可以发现对于这样一个串：

原串：xxxxxxxxxx

新串：#x#x#x#x#x#x#x#x#x#x#

我们可以观察到，假设这时我们已经求出了f和g，那么对于任意位置而言，合并出的最长双回文串中，都是“偶串”，且有一半是'#',一半是原串。

因此我们可以直接合并f[i-1] 和 g[i],并用ans记录最大值，那么这时真正的答案就是ans / 2.

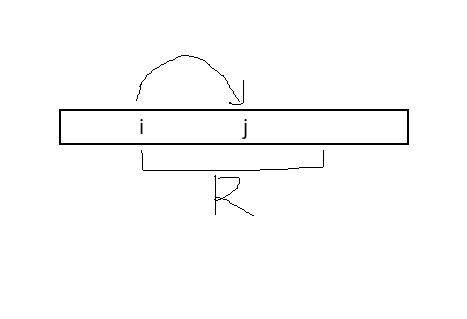
假设我们manacher已经求到了第i位，此时i的最长回文半径是R，且j已经被包括在R里面了，那么显然i对j的贡献是(j - i) * 2 + 1。

而因为贡献只和i与j的位置有关，并且我们的i是从1开始，逐渐递增的，因此对于任意一个j，第一次将它更新的i必然可以产生最优解，因此每个j会且仅会被更新一次。

而被更新的j显然也是递增的，因为如果j后面的k已经被更新的话，说明之前已经有一个i可以使得k被覆盖在内了。那么j既然在k前面，肯定也被覆盖过了，

因此求出f[j]时，j肯定是递增的（也就是说肯定是先求出前面的在求出后面的），因此我们可以直接维护一个指针t（这个指针只是字面上的指针），表示当前已经更新到了t，

一旦被覆盖的MaxRight > t,我们就直接用当前的i来更新t。

对于前缀回文串，我们直接把字符串翻转过来，然后再做一遍相同的操作，再把得到的数组反转回来就可以了

 #include<bits/stdc++.h>
 using namespace std;
 #define R register int
 #define AC 202000
 /*处理出前缀半径和后缀半径，然后合并。可以发现，在扩充了数列之后（#），
 获取的最长双回文串一定是偶串，且# 和 真实字符数量相同。
 因此ans就是合并后的最长长度/2*/
 int n, pos, maxn, ans;
 int f[AC], g[AC], tmp[AC], r[AC];
 char s[AC], p[AC];

 void pre()//读入
 {
     scanf("%s", s + );
     n = strlen(s + );
     for(R i = n; i; --i) s[i * ] = s[i];
     n =  * n + ;
     for(R i = ; i <= n; i += ) s[i] = '#';
     for(R i = ; i <= n; i++) p[i] = s[n - i + ];//把原串倒过来做一遍就是后缀了
     s[] = p[] = '$', s[n + ] = p[n + ] = '$';
 }

 void build()//处理出前缀半径和后缀半径
 {
     int t = ;
     pos = maxn = ;
     for(R i = ; i <= n; i++)
     {
         r[i] = maxn > i ? min(r[ * pos - i], maxn - i + ) : ;
         while(s[i - r[i]] == s[i + r[i]]) ++r[i];
         if(i + r[i] -  > maxn)
         {
             maxn = i + r[i] - , pos = i;
             if(maxn > t)//更新后缀
             {
                 for(R j = t + ; j <= maxn; j++) f[j] = (j - i) *  + ;
                 t = maxn;
             }
         }
     }
     pos = maxn = t = ;
     for(R i = ; i <= n; i++)
     {
         r[i] = maxn > i ? min(r[ * pos - i], maxn - i + ) : ;
         while(p[i - r[i]] == p[i + r[i]]) ++r[i];
         if(i + r[i] -  > maxn)
         {
             maxn = i + r[i] - , pos = i;
             if(maxn > t)//更新后缀
             {
                 for(R j = t + ; j <= maxn; j++) tmp[j] = (j - i) *  + ;
                 t = maxn;
             }
         }
     }
     for(R i = ; i <= n; i++) g[i] = tmp[n - i + ];
 //    for(R i = 1; i <= n; i++) printf("%d ", f[i]);
 //    printf("\n");
 }

 inline void upmax(int &a, int b)
 {
     if(b > a) a = b;
 }

 void work()//合并
 {
     for(R i = ; i <= n; i++)
         upmax(ans, f[i - ] + g[i]);
     printf("%d\n", ans/);
 }

 int main()
 {
     freopen("in.in", "r", stdin);
     pre();
     build();
     work();
     fclose(stdin);
     return ;
 }