POJ 1179 IOI1998 Polygon

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5472		Accepted: 2334

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N. 

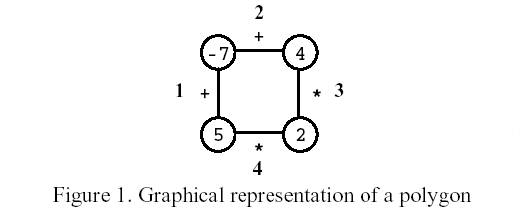
On the first move, one of the edges is removed. Subsequent moves involve the following steps: 
�pick an edge E and the two vertices V1 and V2 that are linked by E; and 
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2. 
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.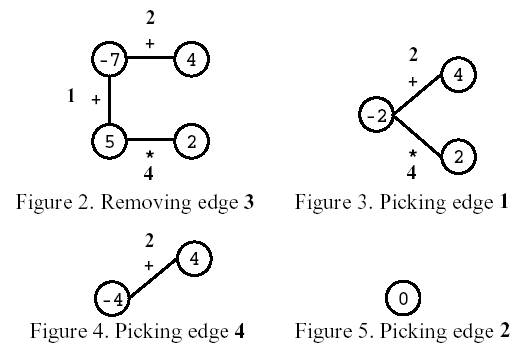 

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score. 

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50 
For any sequence of moves, vertex labels are in the range [-32768,32767]. 

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

Source

IOI 1998

大概就是一个比较简单的dp，枚举中间断开的位置，唯一注意的就是要维护两个值最大值和最小值，因为存在一种情况最小值*最小值反而负负得正了。

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 const int N =  +  ;
 using namespace std ;
 int n,a[N];
 char ss[N];
 long long f[N][N],g[N][N],ans;

 void Init()
 {
     scanf("%d",&n);
     for(int i =  ; i <= n ; ++i)
     {
         cin>>ss[i]>>a[i];
         a[n+i]=a[i],ss[n+i]=ss[i];
     }
 }

 void Solve( )
 {
     for(int i =  ; i <= (n<<) ; ++i) for(int j =  ; j <= (n<<) ; ++j)f[i][j] = -0x3f3f3f3f ;
     for(int i =  ; i <= (n<<) ; ++i) for(int j =  ; j <= (n<<) ; ++j)g[i][j] = 0x3f3f3f3f ;
     for(int i =  ; i <= (n<<) ; ++i)
     {
         if(ss[i+]=='t')
             f[i][i+] = g[i][i+] = a[i] + a[i+];
         else
             f[i][i+] = g[i][i+] = a[i] * a[i+];
          f[i][i] = g[i][i] = a[i];
     }
     long long ans = -0x3f3f3f3f ;
     for(int i = (n<<);--i;)
         for(int j = i +  ; j <=(n<<);++j)
             for(int k = i;k<j;++k)
                 if(ss[k+] == 't')
                 {
                     f[i][j] = max(f[i][j],f[i][k]+f[k+][j]);
                     g[i][j] = min(g[i][j],g[i][k]+g[k+][j]);
                 }
                 else
                 {
                     long long int a = f[i][k]*g[k+][j],b = f[i][k]*f[k+][j];
                     long long int c = g[i][k]*f[k+][j],d = g[i][k]*g[k+][j];
                     f[i][j] = max(f[i][j],max(max(a,b),max(c,d)));
                     g[i][j] = min(g[i][j],min(min(a,b),min(c,d)));
                 }
     for(int i = ; i<= n ;++i)
         ans = max(ans,f[i][i+n-]);
     printf("%lld\n",ans);
     for(int i=;i<=n;++i)
         if(f[i][i+n-] == ans)
             printf("%d ",i);
     puts("");
 }

 int main( )
 {
 //    freopen("polygon.in","r",stdin);
 //    freopen("polygon.out","w",stdout);
     Init();
     Solve();
     fclose(stdin);
     fclose(stdout);
     return  ;
 }