POJ_1631_Bridging_Signals_(动态规划,LIS)

描述

---

http://poj.org/problem?id=1631

铁路左右相连,要求去掉一些边,使得剩下的边不交叉,求剩余边数的最大值.

Bridging signals

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 12652		Accepted: 6898

Description

'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without crossing each other, is imminent. Bearing in mind that there may be thousands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?


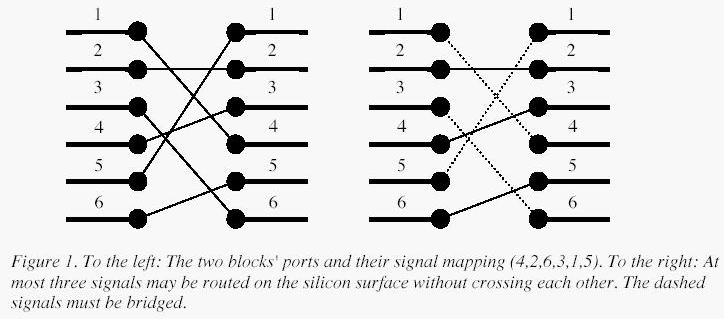
A typical situation is schematically depicted in figure 1. The ports
of the two functional blocks are numbered from 1 to p, from top to
bottom. The signal mapping is described by a permutation of the numbers 1
to p in the form of a list of p unique numbers in the range 1 to p, in
which the i:th number specifies which port on the right side should be
connected to the i:th port on the left side.Two signals cross if and
only if the straight lines connecting the two ports of each pair do.

Input

On
the first line of the input, there is a single positive integer n,
telling the number of test scenarios to follow. Each test scenario
begins with a line containing a single positive integer p < 40000,
the number of ports on the two functional blocks. Then follow p lines,
describing the signal mapping:On the i:th line is the port number of the
block on the right side which should be connected to the i:th port of
the block on the left side.

Output

For
each test scenario, output one line containing the maximum number of
signals which may be routed on the silicon surface without crossing each
other.

Sample Input

4
6
4
2
6
3
1
5
10
2
3
4
5
6
7
8
9
10
1
8
8
7
6
5
4
3
2
1
9
5
8
9
2
3
1
7
4
6

Sample Output

3
9
1
4

Source

Northwestern Europe 2003

分析

---

当去掉一些边,剩下的边不交叉时,对于左边第 i 的连有边的点,设它连的右边的点为 k , 那么左边第 ( i+1 ) 个连有边的点连的右边的点为了保证边不交叉,一定在 k 的下面.这样的话剩下的边连接的右边的点就是单增的.问题就转化为求边的最长上升子序列.

 #include<cstdio>
 #include<algorithm>
 #define read(a) a=getnum()
 #define for1(i,a,n) for(int i=(a);i<=(n);i++)
 using namespace std;

 const int maxn=,INF=0x7fffffff;
 int q,n;
 int a[maxn],dp[maxn];

 inline int getnum(){ int r=,k=;char c;for(c=getchar();c<''||c>'';c=getchar()) if(c=='-') k=-;for(;c>=''&&c<='';c=getchar()) r=r*+c-''; return r*k; }

 int bsearch(int l,int r,int v)
 {
     while(l<r)
     {
         int m=l+(r-l)/;
         if(dp[m]>=v) r=m;
         else l=m+;
     }
     return l;
 }

 void solve()
 {
     for1(i,,n+) dp[i]=INF;
     for1(i,,n)
     {
         int idx=bsearch(,n,a[i]);
         dp[idx]=a[i];
     }
     int ans=bsearch(,n+,INF)-;
     printf("%d\n",ans);
 }

 void init()
 {
     read(q);
     while(q--)
     {
         read(n);
         for1(i,,n) read(a[i]);
         solve();
     }
 }

 int main()
 {
 #ifndef ONLINE_JUDGE
     freopen("bridge.in","r",stdin);
     freopen("bridge.out","w",stdout);
 #endif
     init();
 #ifndef ONLINE_JUDGE
     fclose(stdin);
     fclose(stdout);
     system("bridge.out");
 #endif
     return ;
 }