Sigma Function （LightOJ - 1336）【简单数论】【算术基本定理】【思维】

Sigma Function （LightOJ - 1336）【简单数论】【算术基本定理】【思维】

标签： 入门讲座题解 数论

---

题目描述

Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer is



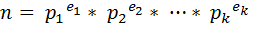
Then we can write,



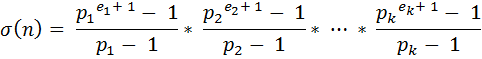
For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 1012).

Output

For each case, print the case number and the result.

Sample Input

4

3

10

100

1000

Sample Output

Case 1: 1

Case 2: 5

Case 3: 83

Case 4: 947

---

题意

约数和函数$$\sigma{(n)} = \sum_{d | n} d;.$$

给定\(n\)，询问\([1, n]\)区间内有几个\(i\)，使得\(\sigma{(i)}\)为偶数？

---

解析

根据算数基本定理，正整数\(n\)，有唯一质因数分解形式，$$n = p_1^{\alpha_1}\cdot p_2^{\alpha_2} \cdot p_3^{\alpha_3} \cdot ,,\cdots ,, \cdot p_n^{\alpha_n}\quad(p_i ;is ;a ;prime).$$

那么，根据乘法计数原理，显然有\(\sigma{(n)} = (1 + p_1^1 + p_1^2 + \cdots p_1^{\alpha_1}) \cdot (1 + p_2^1 + p_2^2 + \cdots + p_2^{\alpha_2}) \cdot (1 + p_3^1 + p_3^2 + \cdots + p_3^{\alpha_3}) \cdot \,\, \cdots \,\, \cdot (1 + p_n^1 + p_n^2 + \cdots + p_n^{\alpha_n})\).

正难则反，我们不方便研究\(\sigma{(n)}\)为偶数的情况，我们可以研究\(\sigma{(n)}\)为奇数的个数，然后用总数减掉奇数个数，就得到偶数个数。

1. 首先，我们要清楚

• 偶数 + 偶数 = 偶数
  
  奇数 + 偶数 = 奇数
  
  奇数 + 奇数 = 偶数

• 偶数 * 偶数 = 偶数
  
  奇数 * 偶数 = 偶数
  
  奇数 * 奇数 = 奇数。

1. 我们知道，只有让\(\sigma{(n)}\)的全部因数都为奇数才可以使\(\sigma{(n)}\)为奇数。

• 若\(2 \,| \,n\)，则\((1 + p_1^1 + p_1^2 + \cdots p_1^{\alpha_1})\)这项一定是奇数。因为\(2\)的任何次幂都是偶数，且偶数 + 奇数 = 奇数。

• 对于除\(2\)以外的其他质数，它的任何次幂都一定是奇数。要想使因数项为奇数，则只能构造($1 + $ 偶数) 的这种形式.当有偶数个奇数相加时，它们的和是偶数。所以，\(\alpha_1,\alpha_2, \alpha_3, \dots,\alpha_n\)（不包括\(2\)的指数）都应该是偶数。

• \(n\) 可以是一个完全平方数。当\(n\)是一个完全平方数时，\(\alpha_1,\alpha_2, \alpha_3, \dots,\alpha_n\)都是偶数。因为\(n\)可以找到两个完全相同的因子。
  
  或者，\(n\)可以是$2 \times $ 完全平方数。因为把\(2\)当作底数的因数项永远是奇数，所以乘上\(2\)依然能保持所有乘数项都是奇数。（为什么没有$2^2, 2^3, 2^4, \dots \times $ 完全平方数？当\(2\)的指数为偶数时，用完全平方数就可以找到这个数。如果是奇数时，指数 = 1 + 偶数，又还原为$2 \times $ 完全平方数。）

• 综上，\(ans = n - \sqrt{n} - \sqrt{n / 2}\)。

---

通过代码

/*
Problem
    LightOJ - 1336
Status
	Accepted
Time
	151ms
Memory
	2084kB
Length
	411
Lang
	C++
Submitted
	2019-11-26 23:30:58
RemoteRunId
	1641328
*/

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int main()
{
    int times, kase = 0;

    scanf("%d", &times);

    while(times --){
        ll n, cnt = 0;                //cnt也有可能会超过1e9，所以要声明为long long类型.
        scanf("%lld", &n);

        for(ll i = 1; i * i <= n; i ++){
            cnt ++;                 //不超过n的完全平方数计数.

            if(2 * i * i <= n)
                cnt ++;             //不超过n/2的完全平方数计数.
        }

        printf("Case %d: %lld\n", ++ kase, n - cnt);
    }

    return 0;
}

---