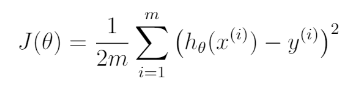【Python】机器学习之单变量线性回归练习(计算Cost Function)
注:练习来自于吴恩达机器学习
翻译后的题目:
你是一个餐厅的老板,你想在其他城市开分店,所以你得到了一些数据(数据在本文最下方),数据中包括不同的城市人口数和该城市带来的利润。第一列是城市的人口数,第二列是在这个城市开店所带来的利润数。
现在,假设θ0和θ1都是0,计算CostFunction,即计算损失函数
首先,本题线性回归的公式应该是这样的:
H(θ) = θ0 + θ1*X
简单的来说,本题中,θ0和θ1都为0,即求H(θ) = 0的损失值,
然后我们再给出损失的定义:
损失,通俗的来讲,即你预测值和给定值的差
这样就得出了损失函数J(θ)的定义:
m为数据的总条数,即m代表有几条数据。
第一步,导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
第二步,把数据读入,然后把图打出来看一下:
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12, 8))
plt.show()
图:
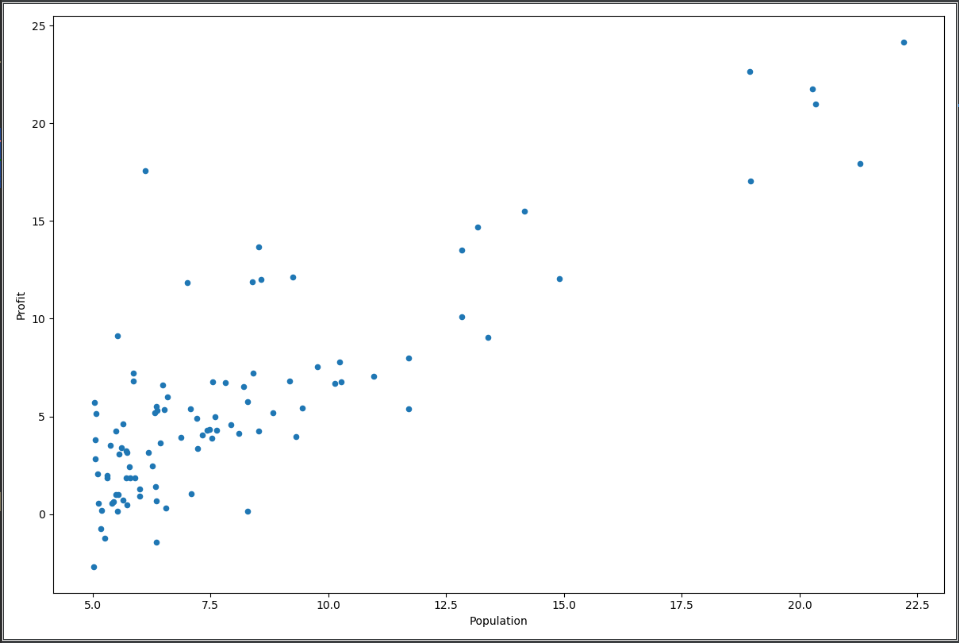
第三步,定义一下costFunction
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
第四步,然后把X从data分出来,Y从data分出来,在X的左边再加一列1,
分出来后的结果为,X为97行2列,Y为97行1列,θ为1行2列,
costFunction是计算矩阵X*矩阵θ的转置得到的值来和真实的Y值比较,计算Cost
data.insert(0, 'Ones', 1)
rows = data.shape[0]
cols = data.shape[1]
X = data.iloc[:, 0:cols - 1]
Y = data.iloc[:, cols - 1:cols]
theta = np.mat('0,0')
X = np.mat(X.values)
Y = np.mat(Y.values) cost = computeCost(X, Y, theta)
print(cost)
标准答案:
32.072733877455676
附数据集ex1data1.txt
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
7.4764,4.3483
8.5781,12
6.4862,6.5987
5.0546,3.8166
5.7107,3.2522
14.164,15.505
5.734,3.1551
8.4084,7.2258
5.6407,0.71618
5.3794,3.5129
6.3654,5.3048
5.1301,0.56077
6.4296,3.6518
7.0708,5.3893
6.1891,3.1386
20.27,21.767
5.4901,4.263
6.3261,5.1875
5.5649,3.0825
18.945,22.638
12.828,13.501
10.957,7.0467
13.176,14.692
22.203,24.147
5.2524,-1.22
6.5894,5.9966
9.2482,12.134
5.8918,1.8495
8.2111,6.5426
7.9334,4.5623
8.0959,4.1164
5.6063,3.3928
12.836,10.117
6.3534,5.4974
5.4069,0.55657
6.8825,3.9115
11.708,5.3854
5.7737,2.4406
7.8247,6.7318
7.0931,1.0463
5.0702,5.1337
5.8014,1.844
11.7,8.0043
5.5416,1.0179
7.5402,6.7504
5.3077,1.8396
7.4239,4.2885
7.6031,4.9981
6.3328,1.4233
6.3589,-1.4211
6.2742,2.4756
5.6397,4.6042
9.3102,3.9624
9.4536,5.4141
8.8254,5.1694
5.1793,-0.74279
21.279,17.929
14.908,12.054
18.959,17.054
7.2182,4.8852
8.2951,5.7442
10.236,7.7754
5.4994,1.0173
20.341,20.992
10.136,6.6799
7.3345,4.0259
6.0062,1.2784
7.2259,3.3411
5.0269,-2.6807
6.5479,0.29678
7.5386,3.8845
5.0365,5.7014
10.274,6.7526
5.1077,2.0576
5.7292,0.47953
5.1884,0.20421
6.3557,0.67861
9.7687,7.5435
6.5159,5.3436
8.5172,4.2415
9.1802,6.7981
6.002,0.92695
5.5204,0.152
5.0594,2.8214
5.7077,1.8451
7.6366,4.2959
5.8707,7.2029
5.3054,1.9869
8.2934,0.14454
13.394,9.0551
5.4369,0.61705
ex1data1.txt
【Python】机器学习之单变量线性回归练习(计算Cost Function)的更多相关文章
- 【Python】机器学习之单变量线性回归 利用批量梯度下降找到合适的参数值
[Python]机器学习之单变量线性回归 利用批量梯度下降找到合适的参数值 本题目来自吴恩达机器学习视频. 题目: 你是一个餐厅的老板,你想在其他城市开分店,所以你得到了一些数据(数据在本文最下方), ...
- 【Python】机器学习之单变量线性回归 利用正规方程找到合适的参数值
[Python]机器学习之单变量线性回归 利用正规方程找到合适的参数值 本次作业来自吴恩达机器学习. 你是一个餐厅的老板,你想在其他城市开分店,所以你得到了一些数据(数据在本文最下方),数据中包括不同 ...
- 机器学习之单变量线性回归(Linear Regression with One Variable)
1. 模型表达(Model Representation) 我们的第一个学习算法是线性回归算法,让我们通过一个例子来开始.这个例子用来预测住房价格,我们使用一个数据集,该数据集包含俄勒冈州波特兰市的住 ...
- 机器学习 (一) 单变量线性回归 Linear Regression with One Variable
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang的个人笔 ...
- 吴恩达机器学习(二) 单变量线性回归(Linear Regression with one variable)
一.模型表示 1.一些术语 如下图,房价预测.训练集给出了房屋面积和价格,下面介绍一些术语: x:输入变量或输入特征(input variable/features). y:输出变量或目标变量(out ...
- python 单变量线性回归
单变量线性回归(Linear Regression with One Variable)¶ In [54]: #初始化工作 import random import numpy as np imp ...
- 【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 2_Linear regression with one variable 单变量线性回归
Lecture2 Linear regression with one variable 单变量线性回归 2.1 模型表示 Model Representation 2.1.1 线性回归 Li ...
- 机器学习(二)--------单变量线性回归(Linear Regression with One Variable)
面积与房价 训练集 (Training Set) Size Price 2104 460 852 178 ...... m代表训练集中实例的数量x代表输入变量 ...
- Coursera《machine learning》--(2)单变量线性回归(Linear Regression with One Variable)
本笔记为Coursera在线课程<Machine Learning>中的单变量线性回归章节的笔记. 2.1 模型表示 参考视频: 2 - 1 - Model Representation ...
随机推荐
- 再谈C#装箱和拆箱操作
1. 使用非泛型集合时引发的装箱和拆箱操作 看下面的一段代码: 1 2 3 4 5 6 7 8 var array = new ArrayList(); array.Add(1); array.Add ...
- KDTree 板子
从杨哥哪里偷的板子, 存一下. #include<bits/stdc++.h> using namespace std; #define Fopen freopen("_in.t ...
- dp递推题2010年吉林省省赛 1456: 逃票的chanming(3)
1456: 逃票的chanming(3) 时间限制: 2 Sec 内存限制: 128 MB提交: 326 解决: 48[提交][状态][讨论版] 题目描述 这是一个神奇的国度. 这个国度一 ...
- Java集合:LinkedList (JDK1.8 源码解读)
LinkedList介绍 还是和ArrayList同样的套路,顾名思义,linked,那必然是基于链表实现的,链表是一种线性的储存结构,将储存的数据存放在一个存储单元里面,并且这个存储单元里面还维护了 ...
- 【1】KNN(K-nearest neighbors algorithm)
基本原理 KNN算法又叫最近邻居法,是一种非常简单易于掌握的分类算法. 其基本原理是,存在一个已知标签的数据集合,也就是训练样本集. 这个样本集中的每一个数据所属的分类都是已知的. 当一个没有标签的新 ...
- 【Offer】[53-2] 【0~n-1中缺失的数字】
题目描述 思路分析 测试用例 Java代码 代码链接 题目描述 一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内.在范围0~n-1内的n个数字中有且只有一个数字 ...
- 【Offer】[18-2] 【删除链表中重复的节点】
题目描述 思路分析 测试用例 Java代码 代码链接 题目描述 在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针. 例如,链表1->2->3- ...
- 056 模块7-os库的基本使用
目录 一.os库基本介绍 二.os库之路径操作 2.1 路径操作 三.os库之进程管理 3.1 进程管理 四.os库之环境参数 4.1 环境参数 一.os库基本介绍 os库提供通用的.基本的操作系统交 ...
- 使用Nginx实现负载均衡(tomcat集群之后实现交叉访问)
tomcat集群(多一台服务器),使用nginx实现负载均衡(upstream sina中配置即可):使用上次博客中的sina案例 1.首先再加一个tomcat服务: 2.修改server.xml配置 ...
- 小白专场-树的同构-c语言实现.md
目录 一.题意理解 二.求解思路 2.1 二叉树表示 2.2 程序框架搭建 2.3 如何建二叉树 2.4 如何判别两二叉树同构 更新.更全的<数据结构与算法>的更新网站,更有python. ...