web-文件上传漏洞总结

思维导图：

一，js验证绕过

1.我们直接删除代码中onsubmit事件中关于文件上传时验证上传文件的相关代码即可。

或者可以不加载所有js，还可以将html源码copy一份到本地，然后对相应代码进行修改，本地提交即可。

2.burp改包，由于是js验证，我们可以先将文件重命名为js允许的后缀名，在用burp发送数据包时候改成我们想要的后缀。

 

二，服务端验证绕过

黑名单

1.上传特殊可解析后缀

可以使用php345，phtml，PHP,phP,等

2.上传.htaccess

我们需要上传一个.htaccess文件，内容为：

SetHandler application/x-httpd-php


上传该apache配置文件，会修改apache的配置，使后面上传的文件都会被看成php文件执行，所以直接上传图片一句话木马

3.后缀大小写绕过

后缀名改为PHP即可

4.空格绕过

黑名单没有对文件中的空格进行处理，使用burpsuite截取数据包，在上传文件后缀名中加空格绕过。

5.点绕过$

windows会对文件中的点进行自动去除，所以可以在文件末尾加点绕过，使用burpsuite抓包在上传文件后缀名中加点绕过

6.::$DATA绕过（windows）

使用burpsuite抓包在上传文件后缀名中加 ::$DATA绕过,使用burpsuite抓包在上传文件后缀名中加::$DATA绕过，1.php::$DATA ==》1.php

7.路径拼接绕过

可以构造文件名1.PHP. . （点+空格+点），经过处理后，文件名变成1.PHP.，即可绕过。

8.双写绕过

可以采用双写绕过：1.pphphp,使用burpsuite抓包在上传文件后缀名该为pphphp

9. 配合解析漏洞，

如apache，1.php.xxx,apache会将该文件后缀名解析为1.php执行

如iis6，使用burpsuite抓包，修改upfile为 。。/1.asp/

　　目录解析(6.0)

　　形式：www.xxx.com/xx.asp/xx.jpg 原理: 服务器默认会把.asp，.asp目录下的文件都解析成asp文件。

　　文件解析

　　如：使用burpsuite抓包，修改upfile为

　　形式：www.xxx.com/xx.asp;.jpg 原理：服务器默认不解析;号后面的内容，因此xx.asp;.jpg便被解析成asp文件了。 解析文件类型

　

　IIS6.0 默认的可执行文件除了asp还包含这三种 :

　　1. /test.asa

　　2./test.cer

　　3./test.cdx

三，白名单绕过

1.mime绕过

通过burpsuite抓包比较上传正常jpg和非法文件php的Content-type的区别

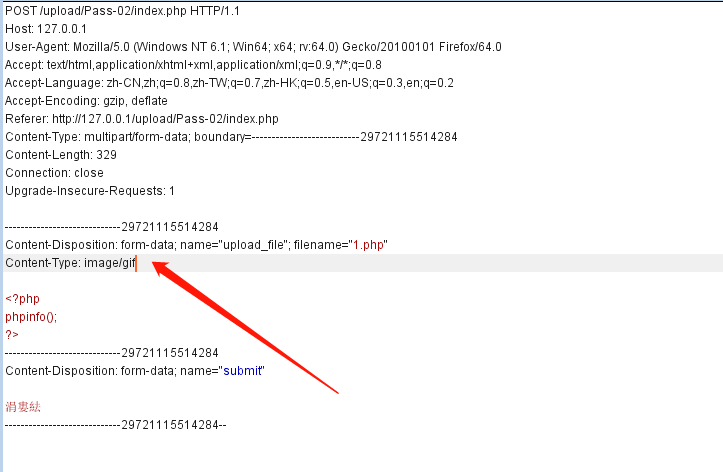
2.%00 截断

使用burpsuite自带工具将00%转换为url编码，如：filename=“1.jpg00%” ==》burpsuite编码后变成1.jpg，forward上传

3.文件幻数检测绕过

在木马内容的前面插入对应的文件头内容，例如：GIF89a ，更保险的方法是在可上传的文件中插入木马代码，然后修改后缀

4.二次渲染绕过

通过例如加载文件进行图像渲染的方式来测试，这个时候就一般需要在正常的文件中插入木马代码了，例如图像，那么插入的代码一般会放在图像的注释区，因此不会影响图像正常渲染绕过这种检测，此时可以使用工具（称为插马器）来进行插入，例如edjpgcom，或者直接用copy命令来合成也可以。当然这种检测不一定能够完全绕过

5.条件竞争

这里先将文件上传到服务器，然后通过rename修改名称，再通过unlink删除文件，因此可以通过条件竞争的方式在unlink之前，访问webshell。