Java中浮点数的基础知识

偶然查看Math.round的JDK

  public static int round(float a) {
         if (a != 0x1.fffffep-2f) // greatest float value less than 0.5
             return (int)floor(a + 0.5f);
         else
             return 0;
     }

注释说0x1.fffffep-2f是最接近0.5的float类型的小数，咦，科学计数法用e表示指数我是知道的，但是这个p是什么鬼。可能有的读者还会问，为什么这个数时最接近0.5的数，这个数到底是多少呢？所以现在的问题有两个：

1、p代表什么。

2、0x1.fffffep-2f 用十进制表示到底是多少。

先公布答案，P在16进制表示的浮点数中代替e作为科学计数法指数部分的标志，1.fffffep-2f中的e是十六进制中的14;第二个问题很简单，也很复杂。说它简单是因为只需要几行代码就可以知道该值是多少。

System.out.println( 0x1.fffffep-2f);
BigDecimal bigDecimal=new BigDecimal(0x1.fffffep-2f);
System.out.println(bigDecimal.toPlainString());

/*输出
0.49999997
0.4999999701976776123046875

说它复杂是理解它为什么是最近0.5的float数。

1、P究竟是什么

原来为了和十六进制中的e进行区分，在java中用16进制表示的浮点数，我们用P代替e作为指数的标志。所以该常数代表0x1.fffffe * 2^(-2),f(F)是float后缀，不写代表是double类型。

A floating-point literal has the following parts: a whole-number part, a decimal or hexadecimal point (represented by an ASCII period character), a fractional part, an exponent, and a type suffix. A floating point number may be written either as a decimal value or as a hexadecimal value. For decimal literals, the exponent, if present, is indicated by the ASCII letter e or E followed by an optionally signed integer. For hexadecimal literals, the exponent is always required and is indicated by the ASCII letter p or P followed by an optionally signed integer.

参考链接:https://stackoverflow.com/questions/8603232/p-in-constant-declaration/8603263#8603263(中文版Java语言规范3.10.2)

2、为什么是最接近0.5的数

任意一个二进制浮点数V可以表示成下面的形式：

　

　　（1）(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。

　　（2）M表示尾数，范围是[1,2)(规格化)或者是[0,1)(非规范化)。

　　（3）2^E表示阶码。

IEEE 754规定，对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。e代表指数部分的无符号数e_k-1e_k-2...e₀,f代表尾数部分的无符号数表示,0.f_n-1...f₁f_0。

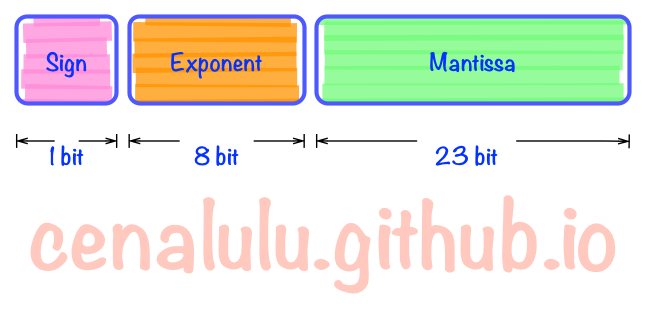
对于exp非零的数即规格化数而言，指数部分的取值范围E=e-127，是[-126,127],尾数部分是[1,2-2^(-23)](M=1+f)。

要得到最接近0.5的数，我们不能用1*2(-1)，因为是完全相等。退而求其次，我们用2-2^(-23)*2(-2)，一个非常接近2的数(3.9999998)除以4来表示0.5无疑是最正确的选择。

看到这里细心的读者可能会问，为什么不用一个非常接近4的数去除以8来到答案呢？无论十六进制浮点数写成0x1.fffffep2这种形式，还是写成0x3.3fffff这种尾数大于2的，Java内部都会通过调整阶码自动将尾数部分控制在[1,2)之间。所以无论使用3.99999(近似表示，下同)除以8还是7.9999999除以16，最后都要表示为一个尾数在[1,2)范围内，乘以一个阶码。换句话说，无论是用3.99999除以8还是7.9999999除以16最终的结果都是一样的。为了看起来比较直观，避免尾数转换之后精度丢失的麻烦，我们直接将尾数固定在[1,2)去确定阶码无疑是最正确的选择。

0x1.fffffep-2f二进制表示是 0 11111100 1111 1111 1111 1111 1111 111。

我们可以猜想对于double类型最接近0.5的数而言，应该同样是尾数全是1，阶码为-2。即为0x1.fffffffffffffp-2。

 public static long round(double a) {
        if (a != 0x1.fffffffffffffp-2) // greatest double value less than 0.5
            return (long)floor(a + 0.5d);
        else
            return 0;
    }

查看JDK,果不其然,说明我的分析是没有问题的。

(以上基础知识来自《深入理解计算机系统》2.4.2)