UVa 11149 矩阵的幂（矩阵倍增法模板题）

https://vjudge.net/problem/UVA-11149

题意：

输入一个n×n矩阵A，计算A+A^2+A^3+...A^k的值。

思路：

矩阵倍增法。

处理方法如下，一直化简下去直到变成A。

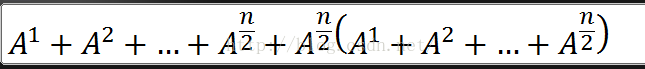
代码如下：

 Matrix solve(Matrix base,int x)
 {
     if(x==)return base;
     Matrix temp=solve(base,x/);
     Matrix sum=add(temp,multi(pow(base,x/),temp));
     if(x&)
         sum=add(pow(base,x),sum);
     return sum;
 }

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 using namespace std;

 const int maxn=+;
 const int MOD=;

 int n,k;

 struct Matrix
 {
     int mat[maxn][maxn];
 }base;

 Matrix multi(Matrix a,Matrix b)
 {
     Matrix temp;
     for(int i=;i<n;i++)
     for(int j=;j<n;j++)
     {
         temp.mat[i][j]=;
         for(int k=;k<n;k++)
             temp.mat[i][j]=(temp.mat[i][j]+a.mat[i][k]*b.mat[k][j])%MOD;
     }
     return temp;
 }

 Matrix pow(Matrix a,int x)
 {
     Matrix res;
     memset(res.mat,,sizeof(res.mat));
     for(int i=;i<n;i++)  res.mat[i][i]=;
     while(x)
     {
         if(x&)  res=multi(res,a);
         a=multi(a,a);
         x>>=;
     }
     return res;
 }

 Matrix add(Matrix a,Matrix b)
 {
     Matrix temp;
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
         temp.mat[i][j]=(a.mat[i][j]+b.mat[i][j])%MOD;
     return temp;
 }

 Matrix solve(Matrix base,int x)
 {
     if(x==)return base;
     Matrix temp=solve(base,x/);
     Matrix sum=add(temp,multi(pow(base,x/),temp));
     if(x&)
         sum=add(pow(base,x),sum);
     return sum;
 }

 int main()
 {
     //freopen("D:\\input.txt","r",stdin);
     while(~scanf("%d%d",&n,&k) &&n)
     {
         for(int i=;i<n;i++)
         for(int j=;j<n;j++)
         {
             scanf("%d",&base.mat[i][j]);
             base.mat[i][j]%=MOD;
         }
         Matrix ans=solve(base,k);
         for(int i=;i<n;i++)
         {
             for(int j=;j<n;j++)
             {
                 if(j)  printf(" ");
                 printf("%d",ans.mat[i][j]);
             }
             printf("\n");
         }
         printf("\n");
     }
     return ;
 }