动态规划_01背包问题_Java实现

原文地址：http://blog.csdn.net/ljmingcom304/article/details/50328141

本文出自：【梁敬明的博客】

1.动态规划　　

　　什么是动态规划？动态规划就是将一个大问题不断向下拆分成小问题，直到拆分出的小问题可以求出其解，然后将小问题的解不断的向上合并，最终得到大问题的解决方案。

2.背包问题　　

　　一个旅行者有一个最多能装m公斤的背包，现在有n中物品，每件的重量分别是W1、W2、……、Wn，每件物品的价值分别为C1、C2、……、Cn， 需要将物品放入背包中，要怎么样放才能保证背包中物品的总价值最大？

3.算法分析

　　假设前n个物品，总承重为j，物品的重量为w，其最大价值为v[n,j]。

　　在背包的总承重不变的前提下，一个物品是否放入背包中直接影响到后面的物品是否能放入到背包中，即一个物品很重同事物品价值又很低时，若装入背包中直接导致其他更多的物品无法放入背包中，从而使得背包中的最大总价值变低。

　　当背包的承重为0，或者不将物品放入背包时，背包中的最大总价值均为0，即v[n,0]=v[0,n]=0。

　　放入当前物品n超过背包的最大承重时，则无法将该物品放入背包中，即v[n,j]=v[n-1,j]。　

　　放入当前物品n不超过背包的最大承重时，则当前物品放入背包时的最大价值为vn+v[n-1,j-wn]，不放入背包时的最大价值为v[n-1,j]，因此对于当前物品是否放入背包中所能获得的最大价值为v[n,j]=max{ v[n-1,j],vn+v[n-1,j-wn] }。　

动态规划



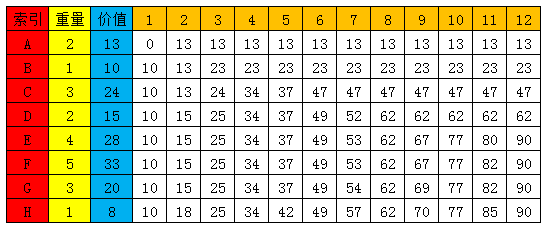
　　上表从上往下，由左至右依次遍历。假设F3的背包承重为3，此时物品的重量为4，所以该物品无法放入背包中，此时背包可以获得的最大总价值为E3的最大总价值25。假设E10的背包承重为10，此时物品的重量为4，所以该物品可以放入背包中，当该物品不放入背包中时，背包的价值为D10的最大价值62，放入背包中时背包的价值为D6的最大价值加上该物品的价值，结果为77，因此最终得出E10的最大价值为77。

　　创建物品对象，存在重量和价值两种属性。

public class Knapsack{
    /** 物品重量 */
    private int weight;
    /** 物品价值 */
    private int value;

    public Knapsack(int weight, int value) {
        this.weight = weight;
        this.value = value;
    }

    public int getWeight() {
        return weight;
    }

    public void setWeight(int weight) {
        this.weight = weight;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

}

　按照动态规划算法将物品放入背包中。

public class DTGHProblem {

    // 所有的物品
    private Knapsack[] bags;
    // 物品的数量
    private int n;
    // 背包总承重
    private int totalWeight;
    // 第一维：当前第几个物品；第二维：当前的背包承重；值：当前背包最大价值
    private int[][] bestValues;
    // 最终背包中最大价值
    private int bestValue;

    public DTGHProblem(Knapsack[] bags, int totalWeight) {
        this.bags = bags;
        this.totalWeight = totalWeight;
        this.n = bags.length;
        if (bestValues == null) {
            // 考虑0的状态+1，防止数组角标越界
            bestValues = new int[n + 1][totalWeight + 1];
        }
    }

    public void solve() {
        // 遍历背包的承重
        for (int j = 0; j <= totalWeight; j++) {
            // 遍历指定物品
            for (int i = 0; i <= n; i++) {
                // 当背包不放入物品或承重为0时，其最大价值均为0
                if (i == 0 || j == 0) {
                    bestValues[i][j] = 0;
                } else {
                    // 如果第 i个物品重量大于总承重，则最优解存在于前 i-1 个背包中
                    if (j < bags[i - 1].getWeight()) {
                        bestValues[i][j] = bestValues[i - 1][j];
                    } else {
                        // 如果第 i个物品不大于总承重，则最优解要么是包含第 i个背包的最优解，
                        // 要么是不包含第 i个背包的最优解， 取两者最大值
                        int weight = bags[i - 1].getWeight();
                        int value = bags[i - 1].getValue();
                        bestValues[i][j] = Math.max(bestValues[i - 1][j], value
                                + bestValues[i - 1][j - weight]);
                    }
                }
            }
        }

        bestValue = bestValues[n][totalWeight];
    }

    public int getBestValue() {
        return bestValue;
    }

}

最终测试结果：90

public class DTGHTest {
public static void main(String[] args) {
    Knapsack[] bags = new Knapsack[] { new Knapsack(2, 13),
            new Knapsack(1, 10), new Knapsack(3, 24), new Knapsack(2, 15),
            new Knapsack(4, 28), new Knapsack(5, 33), new Knapsack(3, 20),
            new Knapsack(1, 8) };
    int totalWeight = 12;
    DTGHProblem problem = new DTGHProblem(bags, totalWeight);

    problem.solve();
    System.out.println(problem.getBestValue());
}
}

欢迎关注我的微信公众号：“”Java面试通关手册（坚持原创，分享美文，分享各种Java学习资源，面试题，以及企业级Java实战项目回复关键字免费领取）：