Gym 102028C - Supreme Command - [思维题][2018-2019 ACM-ICPC Asia Jiaozuo Regional Contest Problem C]

题目链接：https://codeforces.com/gym/102028/problem/C

Lewis likes playing chess. Now he has n rooks on the chessboard with $n$ rows and $n$ columns. All rows of the chessboard are labelled with $1$ through $n$ from top to bottom. All columns of the chessboard are labelled with $1$ through $n$ from left to right. All rooks are labelled with $1$ through $n$ as well. At the very beginning, each row or column contains exactly one rook. However, Lewis allows a square with two or more rooks during the game.

Now he starts to play a game named Supreme Command. He will provide several supreme commands to all rooks. All possible commands are in the following four different formats.

L $k$: Every rook moves k squares to the left;
R $k$: Every rook moves k squares to the right;
U $k$: Every rook moves k squares upward;
D $k$: Every rook moves k squares downward.
For a Supreme Command with given number $k$, if a rook, after moving less than $k$ squares, had arrived at a boundary (which locates in the left-most columns, right-most column, top row or bottom row) such that the rook cannot move further, it would stay there and not move outside the chessboard.

He will also have several queries about rooks. The only two possible formats about queries are listed as follows.

? $k$: Ask the current position of the $k$-th rook;
!: Ask how many pairs of rooks there are currently located in the same square.
Your task in this problem is to answer these queries correctly.

Input

The input contains several test cases, and the first line contains a positive integer $T$ indicating the number of test cases which is up to $1000$.

For each test case, the first line contains two integers $n$ which is described as above, and m indicating the total number of supreme commands and queries, where $1 \le n,m \le 3 \times 10^5$.

Each of the following $n$ lines contains two integers $x$ and $y$, describing a rook located at the intersection of the $x$-th row and the $y$-th column, where $1 \le x,y \le n$.

Then the following $m$ lines describe all Supreme Commands and queries in chronological order, where all given parameters $k$ are integers ranged from $1$ to $n$.

We guarantee that the sum of $n$ and the sum of $m$ in all test cases are up to $10^6$ respectively.

Output

For each test case, output several lines to answer all queries.

For each query of the first type ("? $k$"), output a line containing two integers $x$ and $y$, which indicate the current position of the $k$-th rook is the intersection of the $x$-th row and the $y$-th column. You should output exactly one whitespace between these two numbers.

For each query of the second type ("!"), output a line containing an integer which indicates the number of pairs of rocks that are currently located in the same square.

Example

Input
1
4 9
3 4
2 1
4 2
1 3
L 2
? 1
? 2
R 1
? 1
? 3
!
U 3
!
Output
3 2
2 1
3 3
4 2
0
3

Note

The following figures illustrate the chessboard at the beginning and after each Supreme Commands in the sample case.

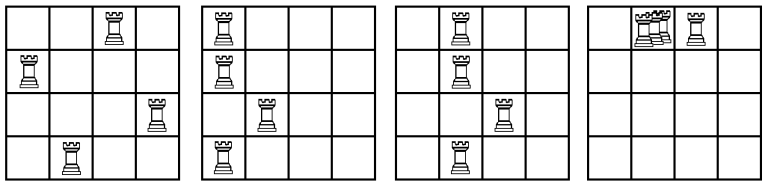
题意：

给定一个 $n \times n$ 的棋盘，记左上角的坐标为 $(1,1)$，右下角的坐标为 $(n,n)$。棋盘上有 $n$ 个编号 $1 \sim n$ 的棋子，每一行或者每一列都有且仅有一个棋子。

给出操作序列，操作有以下三种：

1. $L(R,U,D) \; k$：所有棋子向左（右、上、下）移动 $k$ 格，棋子可以重叠，若操作使棋子向边界外移动则实际上停止不动。
2. $? \; k$：查询编号 $k$ 的棋子现在的位置。
3. $!$：查询现有多少对棋子在同一个格子里。

题解：

这个题，由于可以棋子可以重叠的缘故，不难想到行和列是相互独立的。不妨分开来看，那么问题就从二维的变成了两个一维的合成。

不妨仅仅考虑列坐标，也就是说，在一条横轴上 $1 \sim n$ 这 $n$ 个坐标点上，都放置了一枚棋子。

先考虑怎么查询第 $k$ 个棋子的位置，不妨先记录下其初始位置 $pos_k$，又记 $[L,R]$ 是全体棋子位置的“紧实的”左右边界。

那么，由于移动棋子的操作是所有棋子一起移动。因此，我们不妨把左移所有棋子操作看做把棋盘的左边界 $L$ 往右推动，而把右移所有棋子操作看做把棋盘的右边界 $R$ 往左推动。当然，这样一来 $[L,R]$ 和棋子实际所处区间显然是存在偏差的，可以用一个变量 $\Delta$ 来记录这个偏差。

这样一来，由于 $L$ 只能右移，$R$ 只能左移。也就是说，一颗棋子一旦碰到过边界，就不会再离开边界。因此，我们根据初始位置 $pos_k$，以及目前全体棋子的左右边界 $[L,R]$ 就能判断第 $k$ 枚棋子是否处在边界。当然，我们知道 $[L,R]$ 一旦被往里推动一段距离之后（即 $1 < L \le R < n$），一定范围内的左右移动棋子是不会使得 $[L,R]$ 变小的，这个时候只需要调整一下 $\Delta$ 即可。

接下来，要考虑怎么查询有多少对棋子处在同一个格子内。这个时候不妨重新考虑二维原问题，也就是说现在有上下左右四条边界往里压棋子。那么很显然的，棋子的重叠只可能发生在左上、右上、左下、右下四个角上，且棋子一旦重叠就再也不可能分开。

所以，我们只需要用 $cUL,cUR,cDL,cDR$ 分别维护撞到过上左角、上右角、下左角、下右角的棋子数目即可，并且控制所有棋子只会被计数一次。

这样一来，只需要特判一下所有棋子被压成一行或一列甚至一格的情况，剩下来直接求 $C_{cUL}^2+C_{cUR}^2+C_{cDL}^2+C_{cDR}^2$ 即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3e5+;

ll C[maxn]; //C[n,2]
void prework() {
    for(int i=;i<maxn;i++) C[i]=(ll)i*(i-)/;
}

int n,m;
void Cnt(int id);
struct Sol
{
    int pos[maxn],id[maxn];
    int l,r,d;
    void InitLR() {
        l=, r=n, d=;
    }
    void InitCnt() {
        Cnt(id[]), Cnt(id[n]);
    }
    void SetPos(int p,int i) {
        pos[i]=p, id[p]=i;
    }
    void Left(int k)
    {
        while(l<r && l+d-k<) Cnt(id[++l]);
        if(l+d-k<) d=-l;
        else d-=k;
    }
    void Right(int k)
    {
        while(l<r && r+d+k>n) Cnt(id[--r]);
        if(r+d+k>n) d=n-r;
        else d+=k;
    }
    int Ask(int id)
    {
        if(pos[id]<=l) return l+d;
        if(pos[id]>=r) return r+d;
        return pos[id]+d;
    }
}A,B;

int cLL,cLR,cRL,cRR;
bool vis[maxn];
void Cnt(int id)
{
    if(vis[id]) return;
    else if(A.pos[id]<=A.l && B.pos[id]<=B.l) cLL++, vis[id]=;
    else if(A.pos[id]<=A.l && B.pos[id]>=B.r) cLR++, vis[id]=;
    else if(A.pos[id]>=A.r && B.pos[id]<=B.l) cRL++, vis[id]=;
    else if(A.pos[id]>=A.r && B.pos[id]>=B.r) cRR++, vis[id]=;
}

ll Query()
{
    //printf("上左=%d 上右=%d 下左=%d 下右=%d\n",cLL,cLR,cRL,cRR);
    if(A.l==A.r && B.l==B.r) return C[cLL+cLR+cRL+cRR];
    else if(A.l==A.r) return C[cLL+cRL]+C[cLR+cRR];
    else if(B.l==B.r) return C[cLL+cLR]+C[cRL+cRR];
    else return C[cLL]+C[cLR]+C[cRL]+C[cRR];
}

int main()
{
    prework();
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%d%d",&n,&m);
        A.InitLR(); B.InitLR();
        for(int i=,x,y;i<=n;i++)
        {
            scanf("%d%d",&x,&y);
            A.SetPos(x,i);
            B.SetPos(y,i);
        }

        cLL=cLR=cRL=cRR=;
        memset(vis,,(n+)*sizeof(bool));
        A.InitCnt(); B.InitCnt();

        char op[]; int k;
        while(m--)
        {
            scanf("%s",op);
            if(op[]=='!') printf("%I64d\n",Query());
            else
            {
                scanf("%d",&k);
                if(op[]=='U') A.Left(k);
                if(op[]=='D') A.Right(k);
                if(op[]=='L') B.Left(k);
                if(op[]=='R') B.Right(k);
                if(op[]=='?') printf("%d %d\n",A.Ask(k),B.Ask(k));
            }
        }
    }
}

注：有很多是参考标程的QAQ，要不然感觉自己估计是写不出来的QAQ。