EM算法笔记

EM算法在很多地方都用使用到，比如简单的K-means算法，还有在隐马尔可夫里面，也涉及到了EM算法，可见EM算法在机器学习领域的重要地位。在这里就写一下我对于EM算法的一些理解笔记。后续有新的理解也会追加的。 
EM算法的全称叫做：期望最大。EM算法的想法很简单，就像一个人有两条腿向前走，你总是需要固定一条腿动另一条腿这样交替往前走。这里面的两条腿，一个是隐变量，一个是参数θ。 
在了解EM算法之前，首先需要了解一些基本的概念。

凹凸函数

这个是《最优化》里面的概念，如果它的二阶导大于0，那么就是凸函数；如果是二阶导小于0，那么就是凹函数。（我记得《最优化》数学老师说，高数的定义和最优化的定义是反着的，因为用的概念不一样，高数好像用的是前苏联的定义，最优化是用的欧洲定义。我也不知道是不是真的……）。这样可能不是很容易记住，所以就取两个很有代表性的函数，方便记忆：凸函数：x²，凹函数：−x²。这样，就是你忘记了定义，也很容易通过这两个函数想越来。更重要的是为了方便你理解下面的概念。

Jensen不等式

这个是EM里面，我认为最重要的一个概念，因为它其实是贯穿整个EM的算法里面的。Jensen不等式的概念也很简单，就是如果是凸函数：f(E(x)) < E(f(x));凹函数：f(E(x)) > E(f(x))。这个定义可能一开始没看明白是什么意思，主要问题可能是那个E(x)的期望。换一个简单的说法, 就是如果是凸函数f(x+y2)<f(x)+f(y)2。这里其实是就是把期望这个公式简化成每个变量出现的概率是1/2，然后你把这个画到f(x)=x2里面就一目了然了。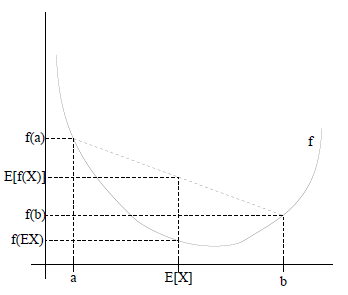

EM算法

给定的训练样本是x(1),...,x(m)，我们希望求出最大的概率p(x;θ)。 
我们可以求出这个模型的最大似然估计：

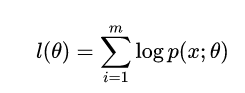
然后取对数：

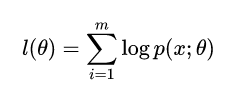
但是，在这个模型里面我们认为p(x;θ)是存在隐变量z的，于是上式改写成

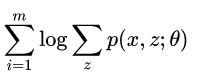
之前求最大似然是很容易，取完对数求导就可以了，但是现在不行，因为有一个隐变量了。那么应该怎么做呢，我们可以固定一个参数，先求另一个参数的最大化，然后再求之前固定的参数。 
但是先固定哪个呢，还是随便固定？（这个问题在K-means里面也有，后面再解释。） 
这里，我们先观察上面那个式子，直接想出θ是不可能了，因为有z。所以如果想求θ，就一定要固定z。那怎么固定z呢？EM算法就用到了Jensen不等式来估计这个这个z。log是一个凹函数，所以上面那个式子根据不等式是存在一个下界的，那么我们就可以通过下界等式成立的情况来求出最大的z对不对？所以我们可以写出

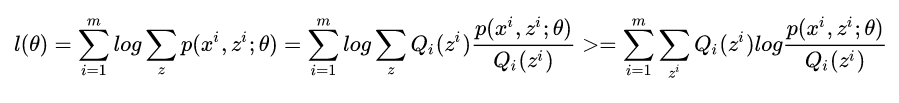
我们可以把jensen的f(x)换log就是上面那个式子了。 
EM算法可以写成：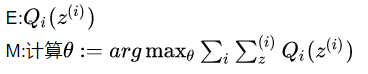 

EM推导

EM要解决两个问题，一个是什么时候等式相等；二是为什么一定收敛。

什么时候等式成立呢？

x=E(x)的时候，你带入就会发现两边等式是相等的。因为都是取那一个点，而且概率也一样，所以自然相等。所以就是p(xi,zi;θ)Qi(z(i))=c 
然后把Q乘过去，并对所有的z求和，得到:

 

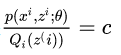
又因为∑_zQi(zi)等于1所以∑_zp(xi,zi;θ)=c 
因此我们可以知道

从这里我们就可以看出，E步计算的Q其实是后验概率。这样可以得到l的下界，然后M步就是把下界提高。如此循环，最终得到最优解。 

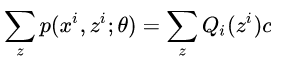
从而EM算法两步可以理解为：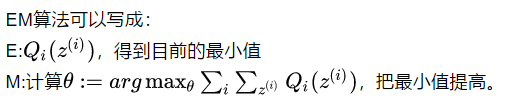 

为什么一定收敛？

其实为什么收敛需要解决的一个问题是，是否是单调，如果是单调的话，就可以通过变化幅度来决定。

之所以l(t)<=l(t+1)是因为在M步的时候，θ让公式变大了。所以既然单调，就可以通过变化来证明收敛。 
其实这两个问题，也是E与M分别需要解决的问题，E就是让等式成立，而M就是让新状态大于旧状态。

参考资料：

http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html 
http://www.csuldw.com/2015/12/02/2015-12-02-EM-algorithms/