bzoj5118: Fib数列2（费马小定理+矩阵快速幂）

　　题目大意：求$fib(2^n)$

　　就是求fib矩阵的(2^n)次方%p，p是质数，根据费马小定理有

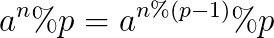
　　注意因为模数比较大会爆LL，得写快速乘法...

#include<bits/stdc++.h>
#define ll long long
#define MOD(x) ((x)>=mod?(x-mod):(x))
using namespace std;
const int maxn=;
const ll mod=;
struct mtx{ll mp[][];mtx(){memset(mp, , sizeof(mp));}}ans, base;
ll n, T;
inline ll mul(ll a, ll b, ll mod)
{
    ll ans=; a%=mod;
    for(;b;b>>=, a=MOD(a+a))
    if(b&) ans=MOD(ans+a);
    return ans;
}
mtx operator*(mtx a, mtx b)
{
    mtx c;
    for(int i=;i<;i++)
    for(int j=;j<;j++)
    for(int k=;k<;k++)
    c.mp[i][j]=MOD(c.mp[i][j]+mul(a.mp[i][k], b.mp[k][j], mod));
    return c;
}
inline ll power(ll a, ll b, ll mod)
{
    ll ans=;
    for(;b;b>>=, a=mul(a, a, mod))
    if(b&) ans=mul(ans, a, mod);
    return ans;
}
inline ll mtx_power(ll b)
{
    if(!b) return ;
    for(;b;b>>=, base=base*base)
    if(b&) ans=ans*base;
    return ans.mp[][];
}
int main()
{
    scanf("%lld", &T);
    while(T--)
    {
        scanf("%lld", &n);
        ll t=power(, n, mod-);
        base.mp[][]=base.mp[][]=base.mp[][]=; base.mp[][]=;
        ans.mp[][]=ans.mp[][]=; ans.mp[][]=ans.mp[][]=;
        printf("%lld\n", mtx_power(t));
    }
}