一只青蛙从第一级台阶跳到第n级，每次可以跳任意级，共有多少种跳法，并写出递推式

是斐波那契数列问题

假设f(n)是n个台阶跳的次数：(假设已经调到第n个台阶，最后一次是由哪个台阶跳上来的)

f(n) = f(n-1)+f(n-2)+...+f(n-(n-1)) + f(n-n) == f(0) + f(1) + f(2) + f(3) + ... + f(n-2) + f(n-1) == f(n) = 2*f(n-1)

所以，可以得出递推式:

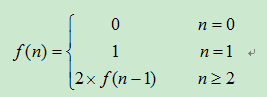
 public static int jumpFloor(int n) {
         if (n <= 0)
             return 0;
         if (n == 1)
             return 1;
         return 2 * jumpFloor(n - 1);
 }

跳台阶，一次只能夸1个、2个和3个台阶，解法类似：

 public static int cnt(int n){
         int[]dic = {0,1,2,4};
         if ( n <= 3)
             return dic[n];
         return cnt(n-1) + cnt(n-2) + cnt(n-3);
 }