机器学习-ID3决策树算法（附matlab/octave代码）

ID3决策树算法是基于信息增益来构建的，信息增益可以由训练集的信息熵算得，这里举一个简单的例子

data=[心情好 天气好  出门

心情好 天气不好 出门

心情不好 天气好 出门

心情不好 天气不好 不出门]

前面两列是分类属性，最后一列是分类

分类的信息熵可以计算得到：
出门=3，不出门=1，总行数=4
分类信息熵 = -(3/4)*log₂(3/4)-(1/4)*log₂(1/4)

第一列属性有两类，心情好，心情不好

心情好 ,出门=2，不出门=0，行数=2

心情好信息熵=-(2/2)*log₂(2/2)+(0/2)*log₂(0/2)

同理

心情不好信息熵=-(1/2)*log₂(1/2)-(1/2)*log₂(1/2)

心情的信息增益=分类信息熵 - 心情好的概率*心情好的信息熵 - 心情不好的概率*心情不好的信息熵

---

由此可以得到每个属性对应的信息熵，信息熵最大的即为最优划分属性。

还是这个例子，加入最优划分属性为心情

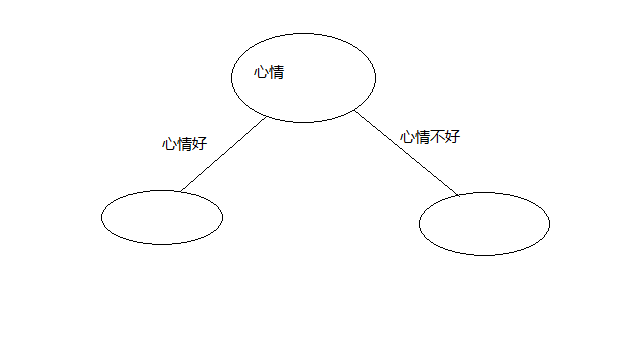
然后分别在心情属性的每个具体情况下的分类是否全部为同一种，若为同一种则该节点标记为此类别，

这里我们在心情好的情况下不管什么天气结果都是出门所以，有了

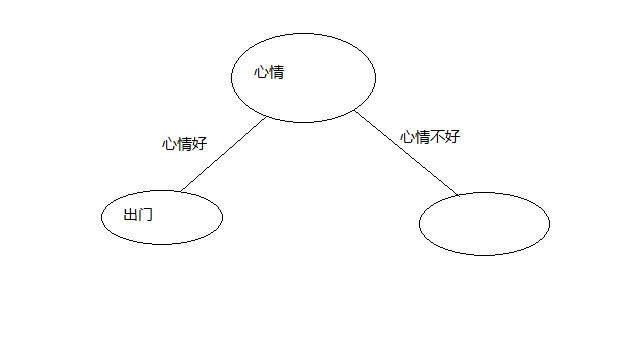
心情不好的情况下有不同的分类结果，继续计算在心情不好的情况下，其它属性的信息增益，

把信息增益最大的属性作为这个分支节点，这个我们只有天气这个属性，那么这个节点就是天气了，

天气属性有两种情况，如下图

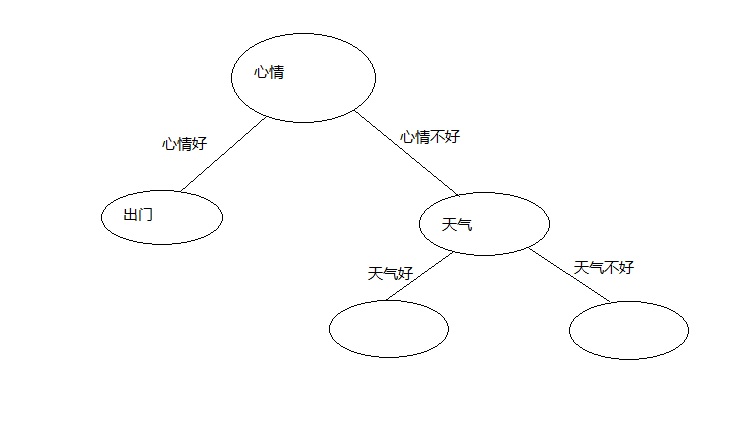
在心情不好并且天气好的情况下，若分类全为同一种，则改节点标记为此类别

有训练集可以，心情不好并且天气好为出门，心情不好并且天气不好为不出门，结果入下图

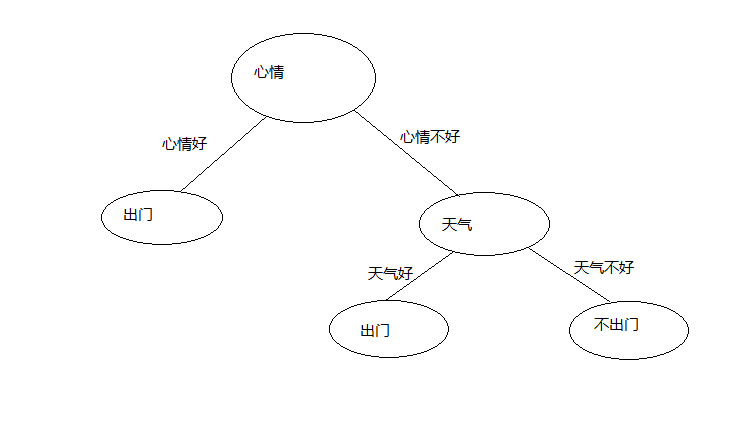
对于分支节点下的属性很有可能没有数据，比如，我们假设训练集变成

data=[心情好 晴天  出门

心情好 阴天 出门

心情好 雨天 出门

心情好 雾天 出门

心情不好 晴天 出门

心情不好 雨天 不出门

心情不好 阴天 不出门]

如下图：

在心情不好的情况下，天气中并没有雾天，我们如何判断雾天到底是否出门呢？我们可以采用该样本最多的分类作为该分类，
这里天气不好的情况下，我们出门=1，不出门=2，那么这里将不出门，作为雾天的分类结果

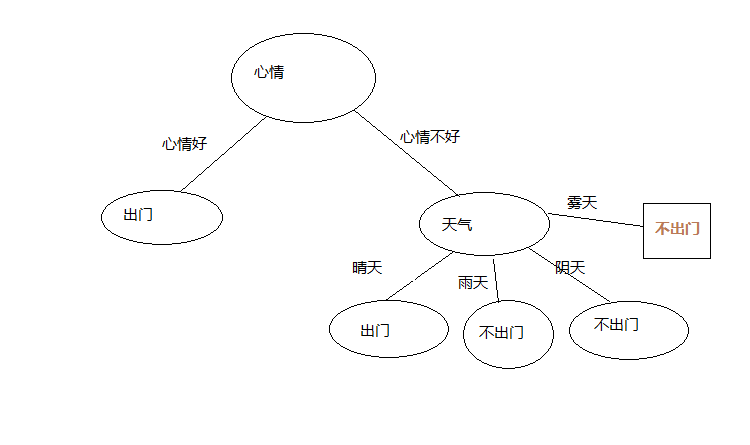
在此我们所有属性都划分了，结束递归，我们得到了一颗非常简单的决策树。

下面附上我的实现ID3决策树算法代码：（octave/matlab，该程序本人已经验证过可以执行且结果正确，这里属性集我偷了一个懒，

没有标识出具体属性名，我是使用矩阵中的列号）

著名的还有C4.5决策树算法，它是ID3的改进，作者都是同一个人，罗斯昆兰

%生成决策树ID3算法
%data:训练集
%feature:属性集
function [node] =createTree(data,feature)
  type=mostType(data);
  [m,n]=size(data);
  %生成节点node
  %value：分类结果，若为null则表示该节点是分支节点
  %name:节点划分属性
  %type:节点属性值
  %children:子节点
  node=struct('value','null','name','null','type','null','children',[]);
  temp_type=data(1,n);
  temp_b=true;
  for i=1:m
    if temp_type!=data(i,n)
      temp_b=false;
    end
  end
  %样本中全为同一分类结果，则node节点为叶子节点
  if temp_b==true
    node.value=data(1,n);
    return;
  end
  %属性集合为空，将结果标记为样本中最多的分类
  if sum(feature)==0
    node.value=type;
    return;
  end
  feature_bestColumn=bestFeature(data);
  best_feature=getData()(:,feature_bestColumn);
  best_distinct=unique(best_feature);
  best_num=length(best_distinct);
  best_proc=zeros(best_num,2);
  best_proc(:,1)=best_distinct(:,1);
  %循环该属性的每一个值
  for i=1:best_num
    Dv=[];
    Dv_index=1;
    %为node创建一个bach_node分支，设样本data中改属性值为best_proc(i,1)的集合为Dv
    bach_node=struct('value','null','name','null','type','null','children',[]);
    for j=1:m
      if best_proc(i,1)==data(j,feature_bestColumn)
        Dv(Dv_index,:)=data(j,:);
        Dv_index=Dv_index+1;
      end
    end
    %Dv为空则将结果标记为样本中最多的分类
    if length(Dv)==0
      bach_node.value=type;
      bach_node.type=best_proc(i,1);
      bach_node.name=feature_bestColumn;
      node.children(i)=bach_node;
      return;
    else
      feature(feature_bestColumn)=0;
      %递归调用createTree方法
      bach_node=createTree(Dv,feature);
      bach_node.type=best_proc(i,1);
      bach_node.name=feature_bestColumn;
      node.children(i)=bach_node;
    end
  end
end

%获取最优划分属性
function [column] = bestFeature(data)
  [m,n]=size(data);
  featureSize=n-1;
  gain_proc=zeros(featureSize,2);
  entropy=getEntropy(data);
  for i=1:featureSize
    gain_proc(i,1)=i;
    gain_proc(i,2)=getGain(entropy,data,i);
  end
  for i=1:featureSize
    if gain_proc(i,2)==max(gain_proc(:,2))
      column=i;
      break;
    end
  end
end

%计算样本最多的结果
function [res] = mostType(data)
  [m,n]=size(data);
  res_distinct = unique(data(:,n));
  res_proc = zeros(length(res_distinct),2);
  res_proc(:,1)=res_distinct(:,1);
  for i=1:length(res_distinct)
    for j=1:m
      if res_proc(i,1)==data(j,n)
        res_proc(i,2)=res_proc(i,2)+1;
      end
    end
  end
  for i=1:length(res_distinct)
    if res_proc(i,2)==max(res_proc(:,2))
      res=res_proc(i,1);
      break;
    end
  end
end

%计算信息熵
function [entropy] = getEntropy(data)
  entropy=0;
  [m,n]=size(data);
  label=data(:,n);
  label_distinct=unique(label);
  label_num=length(label_distinct);
  proc=zeros(label_num,2);
  proc(:,1)=label_distinct(:,1);
  for i=1:label_num
    for j=1:m
      if proc(i,1)==data(j,n)
        proc(i,2)=proc(i,2)+1;
      end
    end
    proc(i,2)=proc(i,2)/m;
  end
  for i=1:label_num
    entropy=entropy-proc(i,2)*log2(proc(i,2));
  end
end

%计算信息增益
function [gain] = getGain(entropy,data,column)
  [m,n]=size(data);
  feature=data(:,column);
  feature_distinct=unique(feature);
  feature_num=length(feature_distinct);
  feature_proc=zeros(feature_num,2);
  feature_proc(:,1)=feature_distinct(:,1);
  f_entropy=0;
  for i=1:feature_num
    feature_data=[];
    feature_proc(:,2)=0;
    feature_row=1;
    for j=1:m
      if feature_proc(i,1)==data(j,column)
        feature_proc(i,2)=feature_proc(i,2)+1;
      end
      if feature_distinct(i,1)==data(j,column)
        feature_data(feature_row,:)=data(j,:);
        feature_row=feature_row+1;
      end
    end
    f_entropy=f_entropy+feature_proc(i,2)/m*getEntropy(feature_data);
  end
  gain=entropy-f_entropy;