洛谷 P1383 高级打字机==codevs 3333 高级打字机

P1383 高级打字机

• • 18通过
  • 118提交
• 题目提供者yeszy
• 标签倍增图论高级数据结构福建省历届夏令营
• 难度省选/NOI-

提交该题 讨论 题解 记录

最新讨论

• 暂时没有讨论

题目描述

早苗入手了最新的高级打字机。最新款自然有着与以往不同的功能，那就是它具备撤销功能，厉害吧。

请为这种高级打字机设计一个程序，支持如下3种操作：

1.T x：在文章末尾打下一个小写字母x。(type操作)

2.U x：撤销最后的x次修改操作。（Undo操作）

（注意Query操作并不算修改操作）

3.Q x：询问当前文章中第x个字母并输出。（Query操作）

文章一开始可以视为空串。

输入输出格式

输入格式：

第1行：一个整数n，表示操作数量。

以下n行，每行一个命令。保证输入的命令合法。

输出格式：

每行输出一个字母，表示Query操作的答案。

输入输出样例

输入样例#1：

7
T a
T b
T c
Q 2
U 2
T c
Q 2

输出样例#1：

b
c

说明

【数据范围】

对于40%的数据 n<=200;

对于100%的数据 n<=100000；保证Undo操作不会撤销Undo操作。

<高级挑战>

对于200%的数据 n<=100000；Undo操作可以撤销Undo操作。

<IOI挑战>

必须使用在线算法完成该题。

50分代码（栈模拟）：

#include<cstdio>
using namespace std;
#define N 51000
int top,T;
char st[N];
int main(){
    scanf("%d",&T);
    while(T--){
        char c1[],c2[];int x;
        scanf("%s",c1);
        if(c1[]=='T'){
            scanf("%s",c2);
            st[++top]=c2[];
        }
        if(c1[]=='U'){
            scanf("%d",&x);
            top-=x;
        }
        if(c1[]=='Q'){
            scanf("%d",&x);
            printf("%c\n",st[x]);
        }
    }
    return ;
}

题解：

因为Undo操作只能撤销Type操作，所以Undo x 实际上就是删除文章末尾x个字母。用一个栈即可解决（每个字母最多进出一次）。

<高级挑战>    （考虑到部分选手水平较高，故设此附加题）

本题虽为2012年IOI的题目，但只要使用离线算法，就成为只需noip级别编程水平的题目了。

以下声明一些定义：（对于此类题目以及各种可持久化数据结构的离线解法的思考很有帮助）

版本：接受第1--i个修改操作（包含Type和Undo）后的状态称为版本i。版本0为初始状态。

版本链：一般的数据结构题目只有各种修改命令（比如本题的Type操作），那么所有版本就会呈链状排列。

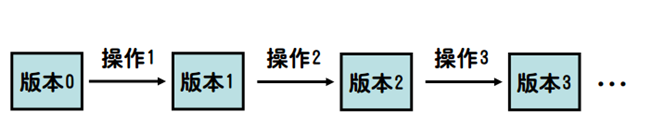
这种情况下只需要设计一个合理的数据结构依次执行操作即可。

版本树：Undo x撤销最近的x次修改操作，实际上就是当前版本还原为x次操作前的版本，换句话说，版本i = 版本i-x-1。

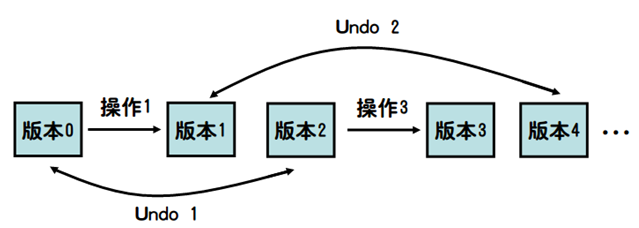
如图所示，所有版本呈树状排列，版本0为根。

读入所有操作并建树，对这颗版本树按欧拉序求出所有版本。上图中就是按0->1->4...4->1->0->2->3->2->0的顺序遍历，同样使用栈就能计算出所有的版本，然后在对应的版本上解决询问即可。

到此，就得到了时空复杂度均为O(n)的离线算法。

能解决这类题目的条件是：

1.允许使用离线算法，进而求出版本树，并允许把询问挂到树的节点上。

2.所有操作都是可逆的。只有所有操作都是可逆的，才能按欧拉序依次求出各版本。如本题的Type操作的逆操作就是弹出栈顶，Undo操作则根本不需要修改（Undo前后2个版本相同）。

相关题目：crisis 60% （2012 国家集训队hw2出题互测\卓亮）

<IOI挑战>

Trie+倍增法寻祖                                       O（nlogn）

各种可持久化数据结构：可持久化块状数组                O（nsqrtn）

可持久化跳表（与Trie解法相近） O（nlogn）

......

因超出noip范围不做更多展开。

AC代码（手写主席树）：

#include<cstdio>
using namespace std;
const int R=1e5,N=(R+)*;
int n,m,now,sz,root[R+],ls[N],rs[N],len[N];
char s[N];
inline int read(){
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
void insert(int &k,int last,int l,int r,int pos,int c){
    k=++sz;
    if(l==r){s[k]=c;return ;}
    ls[k]=ls[last];
    rs[k]=rs[last];
    int mid=l+r>>;
    if(pos<=mid) insert(ls[k],ls[last],l,mid,pos,c);
    else insert(rs[k],rs[last],mid+,r,pos,c);
}
void query(int &k,int last,int l,int r,int pos){
    if(l==r){putchar(s[k]);putchar('\n');return ;}
    int mid=l+r>>;
    if(pos<=mid) query(ls[k],ls[last],l,mid,pos);
    else query(rs[k],rs[last],mid+,r,pos);
}
int main(){
    n=read();
    for(int i=,x;i<=n;i++){
        char op=,ch=;
        for(;op<'A'||op>'Z';op=getchar());
        if(op=='T'){
            for(;ch<'a'||ch>'z';ch=getchar());
            now++;
            len[now]=len[now-]+;
            insert(root[now],root[now-],,R,len[now],ch);
        }
        else if(op=='U'){
            x=read();
            now++;
            root[now]=root[now-x-];
            len[now]=len[now-x-];
        }
        else x=read(),query(root[now],root[now-],,R,x);
    }
    return ;
} 

AC代码（rope标程）：

#include<cstdio>
#include<iostream>
#include<ext/rope>
using namespace std;
using namespace __gnu_cxx;
const int maxn=1e5+;
rope<char> *his[maxn];
int n,m;
inline char getC(){
    for(register char ch=getchar();;ch=getchar()) if((ch>='A'&&ch<='Z')||(ch>='a'&&ch<='z')) return ch;
}
inline int getint(){
    register int x=,f=;
    register char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
int main(){
    n=getint();
    his[]=new rope<char>();
    for(int i=;i<=n;i++){
        char opt=getC();
        if(opt=='T'){
            m++;
            his[m]=new rope<char>(*his[m-]);//就是这一句！它可以实现O(1)的拷贝历史版本，由于rope的底层是平衡树，copy时copy根节点就行了;用它就可以轻松实现可持久化数组
            char x=getC();
            his[m]->push_back(x);
        }else if(opt=='U'){
            int x=getint();
            m++;
            his[m]=new rope<char>(*his[m-x-]);
 
        }else if(opt=='Q'){
            int x=getint()-;
            putchar(his[m]->at(x));
            putchar('\n');
        }
    }
    return ;
}