hdu 4565 So Easy! (共轭构造+矩阵快速幂)

题目链接：

　　http://acm.hdu.edu.cn/showproblem.php?pid=4565

题目大意：

　　给出a，b，n，m，求出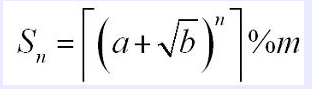的值，

解题思路：

　　因为题目中出现了开根号，和向上取整后求余，所以用矩阵快速幂加速求解过程的时候，会产生误差，就很自然地想到了凑数，因为(a-1)^2<b<a^2,得出0<a-sqrt(b)<1，则无论n取多大，(a-sqrt(b))^n都是小于1的，(a-sqrt(b))^n 与 (a+sqrt(b))^n共轭，两者展开后会相互抵销，所以((a-sqrt(b))^n + (a+sqrt(b))^n)为整数，假设((a-sqrt(b))^n + (a+sqrt(b))^n)用sn表示，则sn*(a+sqrt(b))+(a-sqrt(b)) = S_n+1 - (a^2-b)*S_n-1,进一步得出 S_n+1 = 2*a*S_n - (a*a - b) * S_n-1，

代码：

 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <algorithm>
 #include <iostream>
 #include <cmath>
 #include <queue>
 using namespace std;
 #define LL __int64
 LL a, b, n, m;
 struct mat
 {
     LL p[][];
 };
 
 mat mul (mat x, mat y);
 mat pow (mat x, mat y, LL z);
 
 int main ()
 {
     mat x, y;
     while (scanf ("%I64d %I64d %I64d %I64d", &a, &b, &n, &m) != EOF)
     {
         memset (x.p, , sizeof(x.p));
         memset (y.p, , sizeof(y.p));
         x.p[][] = (*(a*a+b)%m+m)%m;//要用long long，int相乘的时候会溢出
         x.p[][] = (*a) % m;
         y.p[][] = (*a) % m;
         y.p[][] = ;
         y.p[][] = ((b-a*a)%m+m)%m;
         //y.p[1][0] = ((b-a*a)+m)%m;//这样取余是错误的，因为还有可能是负数，害wa了好几次
         x = pow (x, y, n-);
         printf ("%I64d\n", x.p[][]);
     }
     return ;
 }
 
 mat mul (mat x, mat y)
 {
     int i, j, k;
     mat z;
     memset (z.p, , sizeof(z.p));
     for (i=; i<; i++)
         for (j=; j<; j++)
         {
             for (k=; k<; k++)
                  z.p[i][j] += x.p[i][k] * y.p[k][j];
             z.p[i][j] = (z.p[i][j] + m )% m;
         }
     return z;
 }
 mat pow (mat x, mat y, LL z)
 {
     while (z)
     {
         if (z % )
             x = mul(x,y);
         y = mul (y, y);
         z /= ;
     }
     return x;
 }