PCB genesis 大孔扩孔(不用G84命令)实现方法
PCB钻孔时,当钻刀>6.3mm时,超出钻孔范围,钻孔工序是没有这么大的钻刀,当这种情况,工程CAM会都采用G84命令用小孔扩孔的方式制作, 在这里介绍一种如果不用G84命令,用程序实现将大孔生成小孔钻孔达到扩孔的目的。
一.我们先了解一下G84命令扩孔
孔尺寸大小

孔密度

连一篇文章有关于孔数计算方式: https://www.cnblogs.com/pcbren/p/9379178.html
二.求解思路
1.通过孔密度,求出孔与孔中心距离
2.求出单次增量方位角
3.以大孔中心为,长度为(大孔半径-小孔半径), 任选择一个方位角作为起始方位角,并增加一个起始孔,并围绕这个起始方位角不断递增方位角,直到360度递增完成后即结束。
三.C#简易代码实现:
1.扩孔钻孔代码
string drilllayer = "drl";
gLayer layer = g.getFEATURES($"{drilllayer}", g.STEP, g.JOB, "mm", true);
List<gPP> pList = new List<gPP>(); double HoleSize = ; //扩孔所用钻刀大小
foreach (var pad in layer.Plist)
{
if (pad.width > ) //钻孔>6300需扩孔
{
gA arc = calc2.p_2A(new gP(pad.p, pad.width - HoleSize));
arc.width = HoleSize;
var HoleCenterDi = calc2.p_Convex(arc.width * 0.0005)*;
pList.AddRange(calc2.a_2Plist(arc, HoleCenterDi, , true));
}
}
addCOM.pad(pList);
2.计算函数
/// <summary>
/// 通过孔半径与凸高位求 孔中心距
/// </summary>
/// <param name="Rradius">孔半径</param>
/// <param name="tol_">凸位高度值</param>
/// <returns></returns>
public double p_Convex(double Rradius, double tol_ = 0.0127)
{
return Math.Sqrt(Math.Pow(Rradius, ) - Math.Pow(Rradius - tol_, )) * ;
}
/// <summary>
/// 求方位角
/// </summary>
/// <param name="ps"></param>
/// <param name="pe"></param>
/// <returns></returns>
public double p_ang(gPoint ps, gPoint pe)
{
double a_ang = Math.Atan((pe.y - ps.y) / (pe.x - ps.x)) / Math.PI * ;
//象限角 转方位角 计算所属象限 并求得方位角
if (pe.x >= ps.x && pe.y >= ps.y) //↗ 第一象限
{
return a_ang;
}
else if (!(pe.x >= ps.x) && pe.y >= ps.y) // ↖ 第二象限
{
return a_ang + ;
}
else if (!(pe.x >= ps.x) && !(pe.y >= ps.y)) //↙ 第三象限
{
return a_ang + ;
}
else if (pe.x >= ps.x && !(pe.y >= ps.y)) // ↘ 第四象限
{
return a_ang + ;
}
else
{
return a_ang;
}
}//求方位角
/// <summary>
/// 求增量坐标
/// </summary>
/// <param name="ps">起点</param>
/// <param name="val">增量值</param>
/// <param name="ang_direction">角度</param>
/// <returns></returns>
public gPP p_val_ang(gPP ps, double val, double ang_direction)
{
gPP pe = ps;
pe.p.x = ps.p.x + val * Math.Cos(ang_direction * Math.PI / );
pe.p.y = ps.p.y + val * Math.Sin(ang_direction * Math.PI / );
return pe;
}
/// <summary>
/// 弧Arc 转点P组集
/// </summary>
/// <param name="a"></param>
/// <param name="val_">此数值表示:分段数值</param>
/// <param name="type_">代表值数值类型 【0】弧长 【1】角度 【2】弦长 </param>
/// <param name="is_avg">是否平均分布 </param>
/// <returns></returns>
public List<gPP> a_2Plist(gA a, double val_ = 0.1d, int type_ = , bool is_avg = false)
{
List<gPP> list_point = new List<gPP>();
gPP tempP;
tempP.p = a.ps;
tempP.symbols = a.symbols;
tempP.width = a.width;
list_point.Add(tempP); double avg_count;
double angle_val = ;
double rad_ = p2p_di(a.pc, a.pe);
double sum_alge = a_Angle(a);
if (type_ == ) // 【1】角度
{
angle_val = val_;
avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - ; // 总角度/单角度
}
else if (type_ == ) //【2】弦长
{
angle_val = Math.Asin(val_ / (rad_ * )) * / pi;
avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - ; // 总角度/单角度
}
else // 【0】弧长
{
angle_val = val_ * / (pi * rad_);
avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - ; // 总角度/单角度
//avg_count = (int)(Math.Ceiling(a_Lenght(a) / val_)) - 1; // 或 总弧长/单弧长
}
if (is_avg)
angle_val = sum_alge / avg_count;
if (avg_count > )
{
gPP centerP = tempP;
centerP.p = a.pc;
double angle_s = p_ang(a.pc, a.ps);
if (a.ccw) { angle_val = - angle_val; }
for (int i = ; i < avg_count; i++)
{
tempP = p_val_ang(centerP, rad_, angle_s - angle_val * i);
list_point.Add(tempP);
}
}
if (!(zero(a.ps.x - a.pe.x) && zero(a.ps.y - a.pe.y)))
{
tempP.p = a.pe;
list_point.Add(tempP);
}
return list_point;
}
/// <summary>
/// 返回两点之间欧氏距离
/// </summary>
/// <param name="p1"></param>
/// <param name="p2"></param>
/// <returns></returns>
public double p2p_di(gPoint p1, gPoint p2)
{
return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}
/// <summary>
/// 求弧Arc圆心角 //后续改进 用叉积 与3P求角度求解 验证哪个效率高
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
public double a_Angle(gA a)
{
double angle_s, angle_e, angle_sum;
if (a.ccw)
{
angle_s = p_ang(a.pc, a.pe);
angle_e = p_ang(a.pc, a.ps);
}
else
{
angle_s = p_ang(a.pc, a.ps);
angle_e = p_ang(a.pc, a.pe);
}
if (angle_s == ) { angle_s = ; }
if (angle_e >= angle_s)
angle_sum = - Math.Abs(angle_s - angle_e);
else
angle_sum = Math.Abs(angle_s - angle_e);
return angle_sum;
}
/// <summary>
/// 检查值决对值 小于 (eps = 0.001) 浮点误差处理
/// </summary>
/// <param name="x"></param>
/// <returns></returns>
public bool zero(double x)
{
return (((x) > ? (x) : (-x)) < eps);
}
3.Point,PAD,Arc数据结构
/// <summary>
/// 精简 PAD 数据类型
/// </summary>
public struct gPP
{
public gPP(double x_val, double y_val, double width_)
{
this.p = new gPoint(x_val, y_val);
this.symbols = "r";
this.width = width_;
}
public gPP(gPoint p_, double width_)
{
this.p = p_;
this.symbols = "r";
this.width = width_;
}
public gPP(gPoint p_, string symbols_, double width_)
{
this.p = p_;
this.symbols = symbols_;
this.width = width_;
}
public gPoint p;
public string symbols;
public double width;
public static gPP operator +(gPP p1, gPP p2)
{
p1.p += p2.p;
return p1;
}
public static gPP operator +(gPP p1, gPoint p2)
{
p1.p += p2;
return p1;
}
public static gPP operator -(gPP p1, gPP p2)
{
p1.p -= p2.p;
return p1;
}
public static gPP operator -(gPP p1, gPoint p2)
{
p1.p -= p2;
return p1;
}
}
/// <summary>
/// 点 数据类型 (XY)
/// </summary>
public struct gPoint
{
public gPoint(gPoint p_)
{
this.x = p_.x;
this.y = p_.y;
}
public gPoint(double x_val, double y_val)
{
this.x = x_val;
this.y = y_val;
}
public double x;
public double y;
public static gPoint operator +(gPoint p1, gPoint p2)
{
p1.x += p2.x;
p1.y += p2.y;
return p1;
}
public static gPoint operator -(gPoint p1, gPoint p2)
{
p1.x -= p2.x;
p1.y -= p2.y;
return p1;
}
}
/// <summary>
/// ARC 数据类型
/// </summary>
public struct gA
{
public gA(double ps_x, double ps_y, double pc_x, double pc_y, double pe_x, double pe_y, double width_, bool ccw_)
{
this.ps = new gPoint(ps_x, ps_y);
this.pc = new gPoint(pc_x, pc_y);
this.pe = new gPoint(pe_x, pe_y);
this.negative = false;
this.ccw = ccw_;
this.symbols = "r";
this.attribut = string.Empty;
this.width = width_;
}
public gA(gPoint ps_, gPoint pc_, gPoint pe_, double width_, bool ccw_ = false)
{
this.ps = ps_;
this.pc = pc_;
this.pe = pe_;
this.negative = false;
this.ccw = ccw_;
this.symbols = "r";
this.attribut = string.Empty;
this.width = width_;
}
public gPoint ps;
public gPoint pe;
public gPoint pc;
public bool negative;//polarity-- positive negative
public bool ccw; //direction-- cw ccw
public string symbols;
public string attribut;
public double width;
public static gA operator +(gA arc1, gPoint move_p)
{
arc1.ps += move_p;
arc1.pe += move_p;
arc1.pc += move_p;
return arc1;
}
public static gA operator +(gA arc1, gP move_p)
{
arc1.ps += move_p.p;
arc1.pe += move_p.p;
arc1.pc += move_p.p;
return arc1;
}
public static gA operator -(gA arc1, gPoint move_p)
{
arc1.ps -= move_p;
arc1.pe -= move_p;
arc1.pc -= move_p;
return arc1;
}
public static gA operator -(gA arc1, gP move_p)
{
arc1.ps -= move_p.p;
arc1.pe -= move_p.p;
arc1.pc -= move_p.p;
return arc1;
}
}
四.实现效果
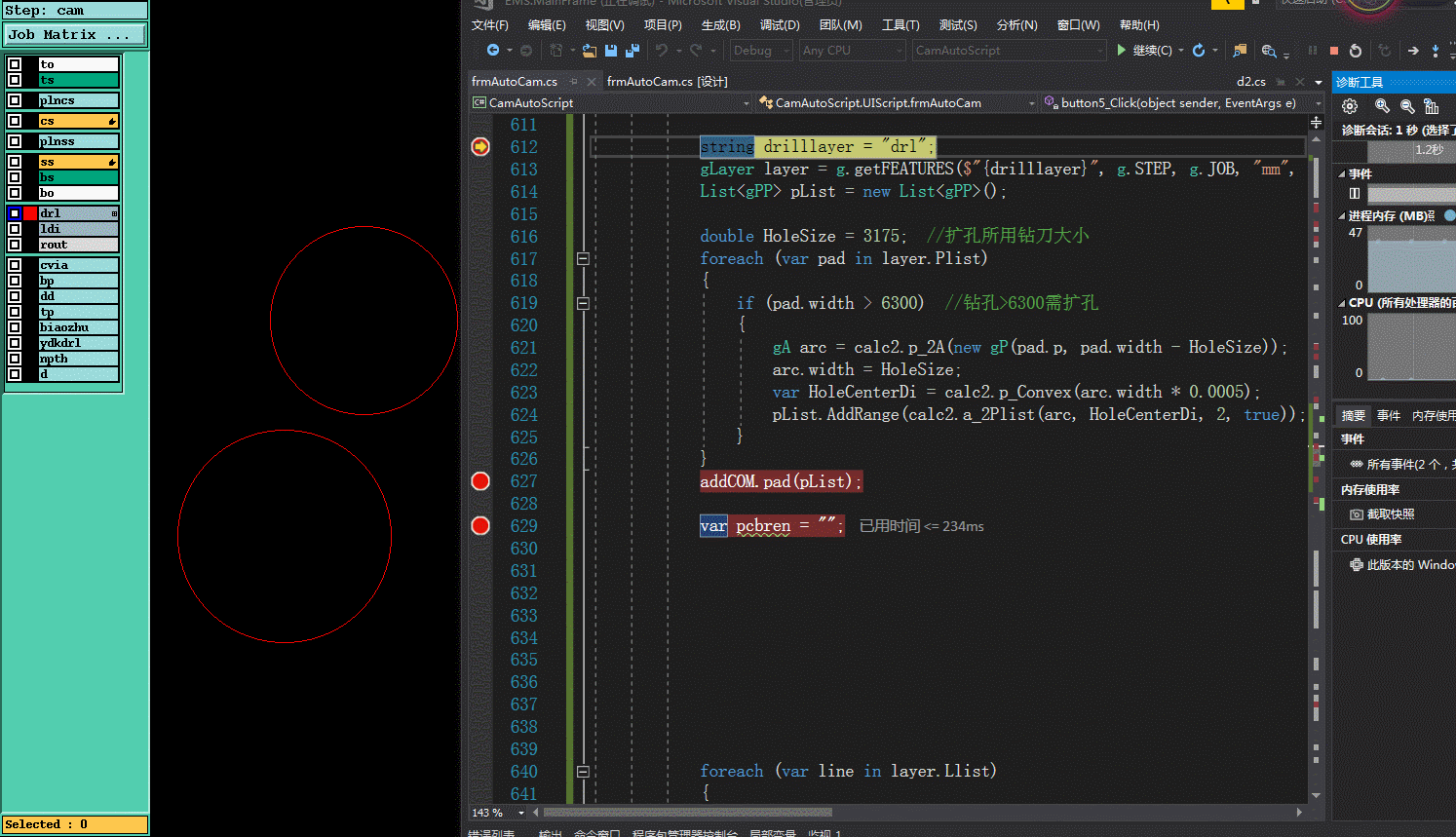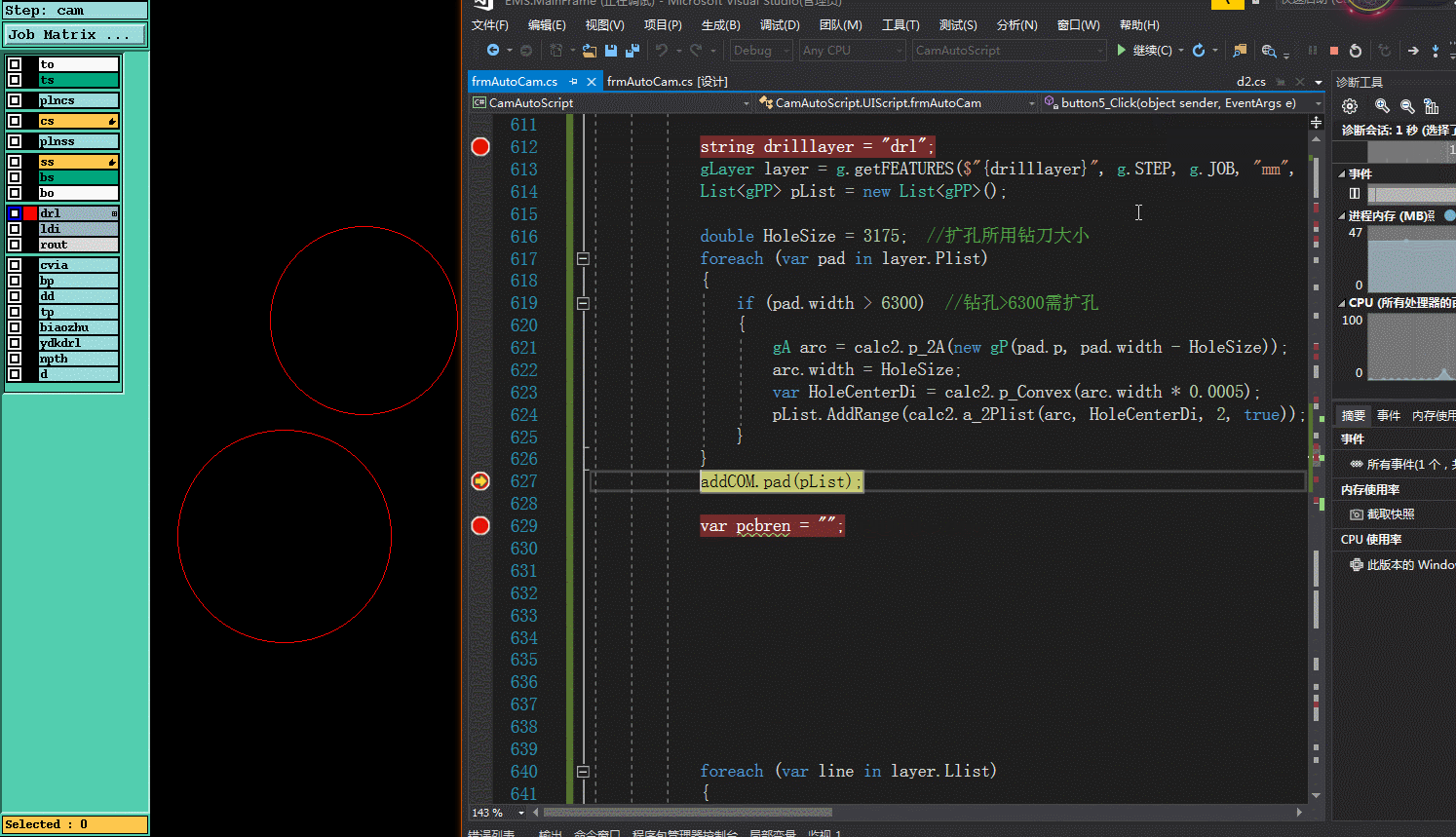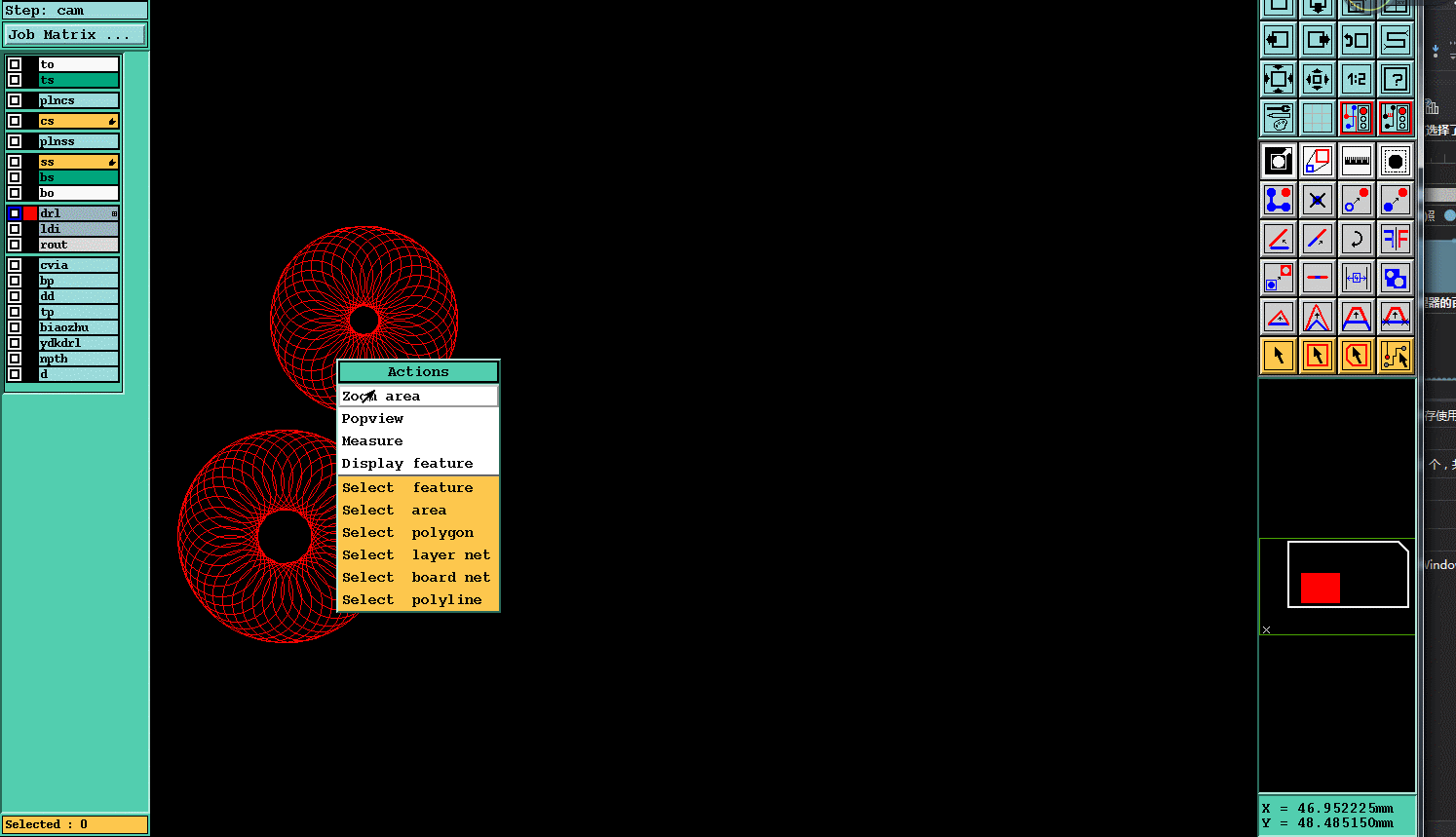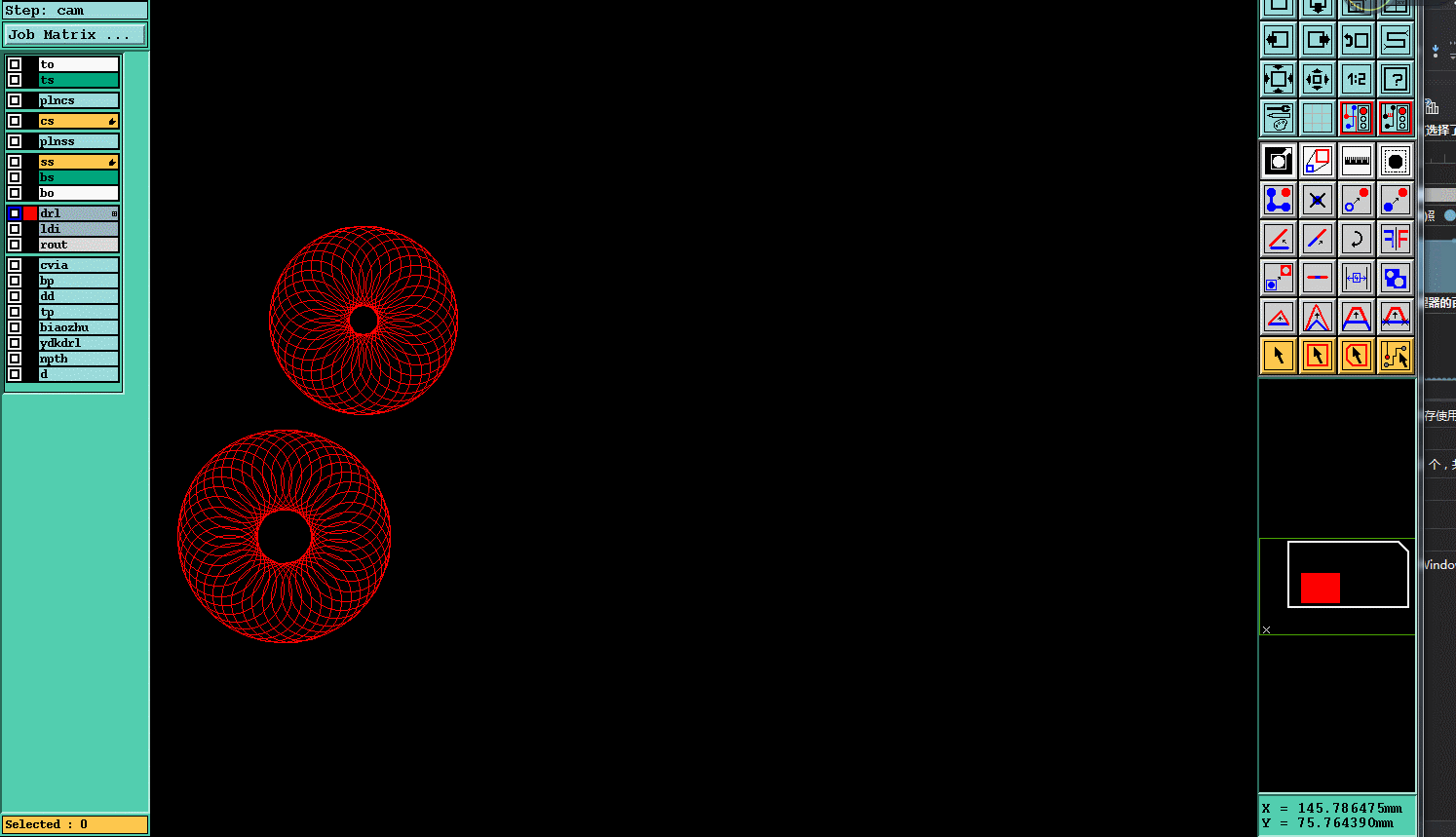
PCB genesis 大孔扩孔(不用G84命令)实现方法的更多相关文章
- PCB genesis大孔加小孔(即卸力孔)实现方法
一.为什么 大孔中要加小孔(即卸力孔) 这其实跟钻刀的排屑有关了,当钻刀越大孔,排屑量也越大(当然这也得跟转速,下刀速的参数有关系),通常当钻刀越大,转速越慢,下刀速也越慢(因为要保证它的排屑通畅). ...
- PCB genesis Slot槽转钻孔(不用G85命令)实现方法
PCB钻Slot槽一般都采用G85命令钻槽孔,而采用G85命令工程CAM无法准确的知道Slot槽钻多少个孔,并不能决定钻槽孔的顺序,因为采用G85命令钻孔密度与钻槽顺序由钻机本身决定的.在这里介绍一种 ...
- PCB genesis自制孔点 Font字体实现方法
一.先看genesis原有Font字体 在PCB工程CAM加孔点字体要求时,通常我们直接用Geneis软件给我们提供了2种孔点字体canned_57与canned_67,但此字体可能不能满足各个工厂个 ...
- PCB genesis连孔加除毛刺孔(槽孔与槽孔)实现方法(三)
一.为什么 连孔加除毛刺孔 原因是 PCB板材中含有玻璃纤维, 毛刺产生位置在于2个孔相交位置,由于此处钻刀受力不均导致纤维切削不断形成毛刺 ,为了解决这个问题:在钻完2个连孔后,在相交处再钻一个孔, ...
- PCB genesis连孔加除毛刺孔(圆孔与槽孔)实现方法(二)
一.为什么 连孔加除毛刺孔 原因是 PCB板材中含有玻璃纤维, 毛刺产生位置在于2个孔相交位置,由于此处钻刀受力不均导致纤维切削不断形成毛刺 ,为了解决这个问题:在钻完2个连孔后,在相交处再钻一个孔, ...
- PCB genesis连孔加除毛刺孔(圆孔与圆孔)实现方法(一)
一.为什么 连孔加除毛刺孔 原因是 PCB板材中含有玻璃纤维, 毛刺产生位置在于2个孔相交位置,由于此处钻刀受力不均导致纤维切削不断形成毛刺 ,为了解决这个问题:在钻完2个连孔后,在相交处再钻一个孔, ...
- PCB genesis孔符制作实现方法
一.先看genesis原始孔符 孔符的作用:用于表示孔径的大小的一种代号, 当孔径检测时,可以按分孔图中的孔符对应的孔径尺寸对孔径检测. 在实际PCB行业通常不使用原始(图形)孔符,而使用字母孔符(如 ...
- PCB Genesis 外形加内角孔实现方法
在PCB工程制作CAM时,经常会遇到外形拐角处直角的,而客户对内角是要求,比如最大内角要求R0.5mm或者不接受内角, 但成型方式为铣方式,又不是啤板成型,那怎么处理才可以达到要求效果呢,在这里介绍2 ...
- Linux 服务器配置、运行、不用敲命令(新手必备!) - 宝塔全攻略建站一条龙
Linux 服务器配置.运行.不用敲命令 WordPress 建站攻略 本文提供全流程,中文翻译. Chinar 坚持将简单的生活方式,带给世人!(拥有更好的阅读体验 -- 高分辨率用户请根据需求调整 ...
随机推荐
- 代码分析工具splint安装介绍
官网 http://www.splint.org/ splint能干什么? splint是一个静态检查C语言代码安全弱点和编写错误的开源程序.(不支持C++) splint会进行多种常规检查,包括 空 ...
- 无插件纯Web HTML5 3D机房 进阶篇(新增设备、线缆、巡查等功能)
前情提要 前阵子写了一篇无插件纯Web 3D机房,介绍了如何用html5在网页上创建无插件的精美3d机房场景.这两个月以来,陆续收到很多朋友的鼓(膝)励(盖),受宠若惊之余,对索要源代码的朋友都已经尽 ...
- linux网络编程——域名转换 gethostbyname与gethostbyaddr
域名转换 #include <netdb.h> struct hostent *gethostbyname(const char *name); 参数: name: 执行主机名的指针 返回 ...
- 爬虫之BeautifulSoup库
文档:https://beautifulsoup.readthedocs.io/zh_CN/latest/ 一.开始 解析库 # 安装解析库 pip3 install lxml pip3 instal ...
- jmeter录制火狐浏览器
昨天看youtube,居然发现有这功能,啊哈哈 听不懂英语 也能有收获. 一.Jmeter 文件中选择Templates->Recording 二.创建之后,自动出现一个模板: 1. Threa ...
- 洛谷 2476 [SCOI2008]着色方案
50%的数据满足:1 <= k <= 5, 1 <= ci <= 3 100%的数据满足:1 <= k <= 15, 1 <= ci <= 5 [题解] ...
- gif & tools
gif & tools https://www.cockos.com/licecap/ https://www.cockos.com/licecap/licecap128-install.ex ...
- HDU 1059 多重背包问题
问题大意: 有价值1-6的六种物品,分别规定其数目,问是否存在一种方法能使这些物品不拆分就能平均分给两个人 #include <cstdio> #include <cstring&g ...
- [luoguP3146] [USACO16OPEN]248(区间DP)
传送门 f[i][j]表示区间 i-j 合并的最大值 转移: 若f[i][k] && f[k+1][j] && f[i][k] == f[k+1][j] --> ...
- java 远程调用
1.webservice (soap+http) -aixs -axis2 -xfire—>cxf 2.webservice问题 -基于xml,xml效率,(数据传输效率,xml序列化效率) - ...
