[ZJOI 2018] 线图

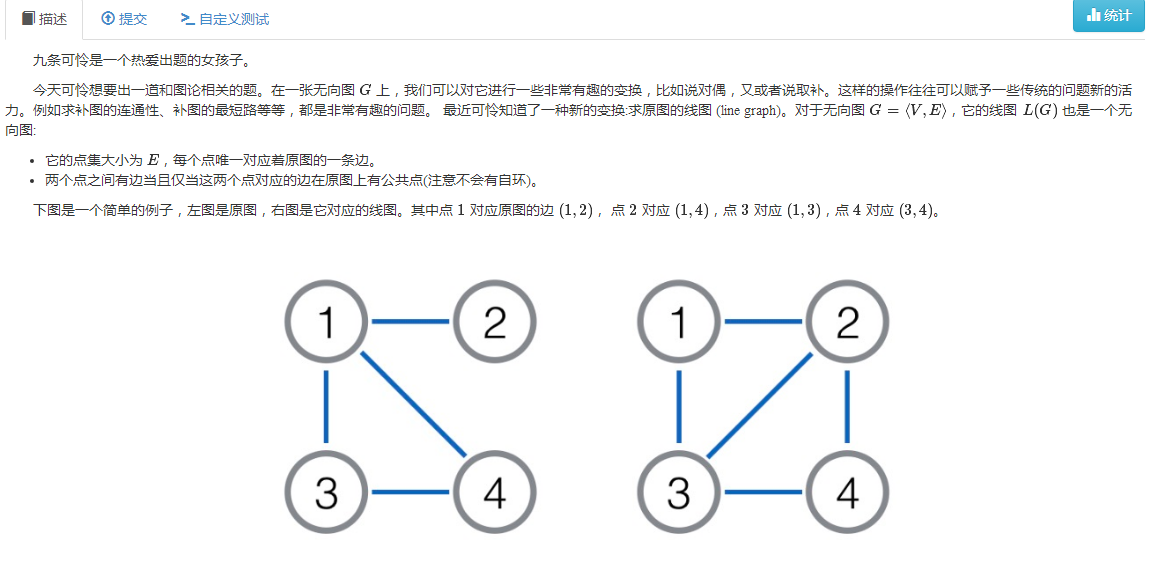
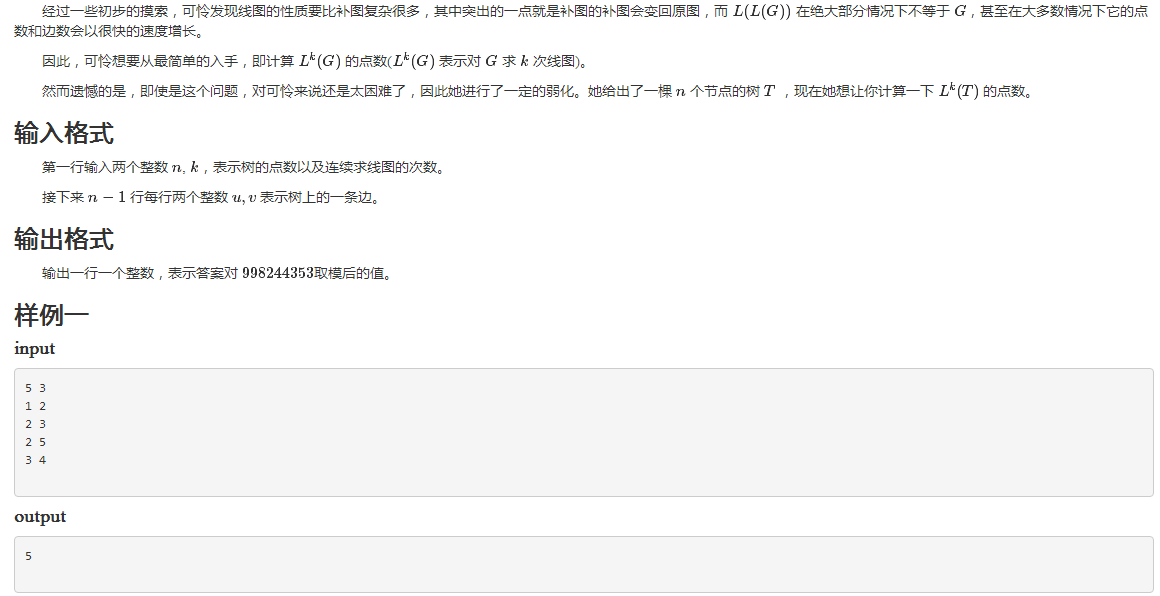
别想多了我怎么可能会正解呢2333，我只会30分暴力(好像现场拿30分已经不算少了2333，虽然我局的30分不是特别难想)。

首先求k次转化的点数显然可以变成求k-1次转化之后的边数，所以我们可以先让k强行减去1，然后再去求k次转化之后的图的边数。

这个时候的k就可能等于1,2,3,4,5,6,7,8，，，还不是很好求。

但是题目中初始给出的图是一颗树啊！也就是说我们完全可以用N^2的代价暴力进行一次转化，因为树只有N-1条边，也就是转化一次之后的图的点数就是N-1，边数最多也是(N-1)*(N-2)/2 [ 考虑菊花图233 ]。

这样再暴力转化一次图后，k的可能取值变成了0，1，2，3，4，5，6，7。

然后此时k=0的数据就可以直接输出转化之后的图的边数了，这没啥好说的。

如果k=1的话，我们只需要知道再转化一次后的图的边数就行了。这里我推了一个结论 : 如果一个图的每个节点i的度数是 D[i] ，那么转化一次之后的图的边数就是 ΣC(D[i],2) 。考虑转化之后的图中的边的两个端点是上一个图中邻接(有公共点)一对边，而且两条边邻接仅会有一个公共点，也就是转化之前的图中每个点的影响是独立的，所以我们直接考虑每个点带来的贡献然后求和一下就好了。

k=2的情况，根据上面的推论，我们只需要知道转化一次之后的图中每个点的度数然后就可以知道转化两次之后的图的边数。显然转化一次之后的图的点的度数就是原图中每条边的邻接的边数，所以我们也可以直接算出边的邻接数然后套用k=1的做法。

我可能是唯一一个没有A题却写博客的人了2333，还是太菜。

#include<bits/stdc++.h>
#define ll long long
const int maxn=5005;
const int ha=998244353;
int n,m,u[maxn],v[maxn],k,deg[maxn];
int ans=0,uu[maxn*maxn],vv[maxn*maxn];
int md[maxn*maxn];

inline int add(int x,int y){
    x+=y;
    return x>=ha?x-ha:x;
}

inline void transform(){
    int N=m,M=0;

    for(int i=1;i<=N;i++)
        for(int j=i+1;j<=N;j++) if(u[i]==u[j]||u[i]==v[j]||v[i]==u[j]||v[i]==v[j]){
            uu[++M]=i,vv[M]=j,deg[i]++,deg[j]++;
        }

    n=N,m=M;
}

inline void calc1(){
    for(int i=1;i<=n;i++) ans=add(ans,deg[i]*(ll)(deg[i]-1)/2%ha);
    printf("%d\n",ans);
}

inline void calc2(){
    for(int i=1;i<=m;i++) md[i]=deg[uu[i]]+deg[vv[i]]-2;
    for(int i=1;i<=m;i++) ans=add(ans,md[i]*(ll)(md[i]-1)/2%ha);
    printf("%d\n",ans);
}

int main(){
    scanf("%d%d",&n,&k),m=n-1,k--;
    for(int i=1;i<=m;i++) scanf("%d%d",u+i,v+i);
    transform(),k--;
    if(!k) printf("%d\n",m);
    else if(k==1) calc1();
    else calc2();
    return 0;
}