数论基础之组合数&计数问题
一.组合数:
问题引入:现在有 n 个球,取其中的 k 个球,问一共有多少
种方式?
答案:
公式直观解释:
我们考虑有顺序地取出 k 个球:第一次有 n 种选择,第二次有 n-1 种
选择,...,第 k 次有 n-k+1 种选择。故一共有

种方案数;但如果不计算顺序的话,那么对于一种方案,其实有 k! 种
不同的顺序,所以再除以 k! 即为最终的答案。
实际编程所需要的公式:C(n,k) = C(n − 1,k) + C(n − 1,k − 1)
题目:
luogu 2822 组合数问题(边计算边模)
luogu 1313 计算系数(答案为:a n × b m × C(k,n))
二.计数问题:
(1). 把 n 个数拆成 k 个非负整数,有多少种方案数?C(n,k)
(2). 把 n 个数拆成 k 个正整数,有多少种方案数?C(n,n-k+1)
1.放球问题:
1. 把 N 个不同的球放在 K 个不同箱子-----n^k
2. N 个相同的球放在 k 个不同的箱子-----C(n,n-k)
3. N 个不同的球放在 k 个相同的箱子
4. N 个相同的球放在 k 个相同的箱子
2.路径行走:
一个 N*M 的网格,每次只能向上或者向右,从左下角到右上角有
多少种方案数
C(n + m − 2,n − 1)
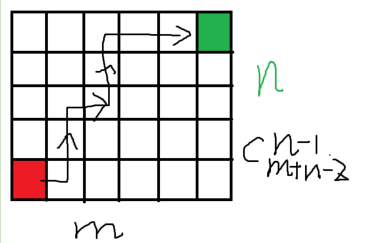
按照字典序的顺序从小写字母 a 开始按顺序给出序列 (序列中都为升序字符串,挑出长度位 L 的字符串有多少个?
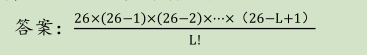
练习:
(1)Codevs 1262 不要把球传我
(2)HDU 5698 瞬间移动
(3)HDU 1465
{
错排公式:设 F[i] 为每个数都不在自己的位置上的排列数。
* 则有公式 F[i] = (n-1) (F[i-1] + F[i-2])
假设在第 1 个位置上的是 k(k ̸= 1),则有两种情况:
1 在 k 的位置上的是 1。则这时候只需要要求其他的 n-2 个数不在
位置上即可。
2 在 k 的位置上不是 1。把 1 看作 k,相当于 n-1 个数都不在自己的
位置上。
}
(4)HDU 4704 Sum
{

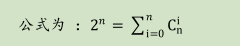
}
数论基础之组合数&计数问题的更多相关文章
- 你也可以手绘二维码(二)纠错码字算法:数论基础及伽罗瓦域GF(2^8)
摘要:本文讲解二维码纠错码字生成使用到的数学数论基础知识,伽罗瓦域(Galois Field)GF(2^8),这是手绘二维码填格子理论基础,不想深究可以直接跳过.同时数论基础也是 Hash 算法,RS ...
- 「kuangbin带你飞」专题十四 数论基础
layout: post title: 「kuangbin带你飞」专题十四 数论基础 author: "luowentaoaa" catalog: true tags: mathj ...
- 数论篇7——组合数 & 卢卡斯定理(Lucas)
组合数 组合数就是高中排列组合的知识,求解组合数C(n,m),即从n个相同物品中取出m个的方案数. 求解方式 求解通式:$C^{m}_{n}=\dfrac {n!}{m!\left( n-m\righ ...
- acm数论之旅--组合数(转载)
随笔 - 20 文章 - 0 评论 - 73 ACM数论之旅8---组合数(组合大法好(,,• ₃ •,,) ) 补充:全错排公式:https://blog.csdn.net/Carey_Lu/ ...
- lightoj1336数论基础
#include<iostream> #include<cstdio> #include<cmath> #define ll long long using nam ...
- 数论基础算法总结(python版)
/* Author: wsnpyo Update Date: 2014-11-16 Algorithm: 快速幂/Fermat, Solovay_Stassen, Miller-Rabin素性检验/E ...
- 从BZOJ2242看数论基础算法:快速幂,gcd,exgcd,BSGS
LINK 其实就是三个板子 1.快速幂 快速幂,通过把指数转化成二进制位来优化幂运算,基础知识 2.gcd和exgcd gcd就是所谓的辗转相除法,在这里用取模的形式体现出来 \(gcd(a,b)\) ...
- 【数论】【组合数】【快速幂】【乘法逆元】洛谷 P2265 路边的水沟
从左上角到右下角,共经过n+m个节点,从其中选择n各节点向右(或者m各节点向下),所以答案就是C(n+m,n)或者C(n+m,m),组合数暴力算即可,但是要取模,所以用了乘法逆元. #include& ...
- 1370 - Bi-shoe and Phi-shoe(LightOJ1370)(数论基础,欧拉函数)
http://lightoj.com/volume_showproblem.php?problem=1370 欧拉函数: 在数论,对正整数n,欧拉函数是少于或等于n的数中与n互质的数的数目. φ(n) ...
随机推荐
- lua-resty-r3 高性能 OpenResty 路由实现
大家下午好!首先做下自我介绍,我于 2014 年加入奇虎 360,后与温铭结识,当时他正在基于 OpenResty 做天擎服务端,用于提供 API 服务.2015 年我们一起写了< OpenRe ...
- E20180423-hm
disclosure n. (发明等的) 公开; 泄露,揭露; 开诚布公的话; 被公开的事情,被披露的秘闻; alignment n. 结盟; 队列,排成直线; 校直,调整; [工] 准线; ali ...
- 51nod 1489 蜥蜴和地下室(dp)
传送门 题意 分析 dp[12][20][20][20]; // dp[a][b][c][d]第a个弓箭手面临第a-1.a.a+1个弓箭手的生命值分别为b.c.d的状态 转移巧妙,需注意 trick ...
- bzoj 1060: [ZJOI2007]时态同步【树形dp】
可能算不上dp,大概是个树形模拟 先一遍dfs算出f[u]为每个点最深的叶子到u的距离,然后再dfs一下,ans加上f[u]-f[e[i].to]-e[i].va,f[u]-f[e[i].to]是这条 ...
- 封装jQuery插件实现TAB切换
先上效果图: 直接上代码: index.html <!DOCTYPE html> <html lang="en"> <head> <met ...
- [HNOI2018]毒瘤
Description 从前有一名毒瘤. 毒瘤最近发现了量产毒瘤题的奥秘.考虑如下类型的数据结构题:给出一个数组,要求支持若干种奇奇怪怪的修改操作(比如区间加一个数,或者区间开平方),并支持询问区间和 ...
- XON/OFF
#define XON 0x11#define XOFF 0x13查找ASCII码表,这两个对应的是DC1(设备控制1)和DC3(设备控制3) X/ON和X/OFF为开启和关闭发送器的信号.X /ON ...
- 前端之CSS语法及选择器
一.css语法: css由两大部分组成:选择符和声明,声明由属性和属性值两部分组成; 选择符{属性:属性值;属性:属性值;} 注: a) 属性和属性值之间用冒号连接: b)每条声明结束要加分号: 二. ...
- 伟景行 citymaker 从入门到精通(1)——js开发,最基本demo,加载cep工程文件
开发环境:citymaker 7(以下简称cm),jquery,easyui 1.4(界面),visual studio 2012(没有vs,不部署到IIS也行,html文件在本地目录双击打开可用) ...
- Ubuntu16下查看CPU、内存和磁盘相关信息
1.内存 查看内存#free -m total used free shared buff/cache available Mem: Swap: 2.CPU 查看逻辑cpu个数: #cat /proc ...
