牛客OI赛制测试赛2（0906）

牛客OI赛制测试赛2（0906）

A ：无序组数

题目描述

给出一个二元组（A,B）

求出无序二元组（a,b） 使得（a|A，b|B）的组数

无序意思就是(a,b)和(b,a) 算一组.

输入描述:

第一行数据组数 T（1≤T≤10000）
接下来T行，每行两个正整数 A,B（1≤A,B≤10000）

输出描述:

共T行，每行一个结果

输入

1
4 6

输出

11

说明

样例解释：
二元组如下：
(1,1)(1,2)(1,3)(1,6)
(2,1)(2,2)(2,3)(2,6)
(4,1)(4,2)(4,3)(4,6)
共12组.
无序二元组如下：

(1,1)(1,2)(1,3)(1,6)
(2,2)(2,3)(2,6)
(4,1)(4,2)(4,3)(4,6)
共11组

分析

1. 给出A的所有因数 和B的所有因数 组成的无序二元组数。无序的意思见题。

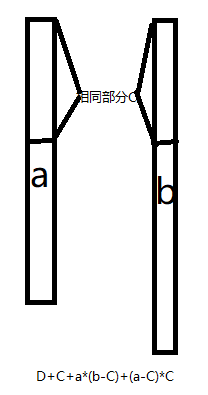
2. 由题意可知，可以产生无序二元组的情况只可能是A和B的公因数，而他们的公因数个数可以由最大公因数gcd(A,B)的因数个数得出，所以我们先打表得出 1~100000 的因数个数。然后由于是产生无序二元组，也就是说，从gcd(A,B) 的因数个数 n 中取两个数进行组合，也就是排列组合问题。直接 D = n*(n-1)/2即可得出。但是要注意，排列组合中不包括两两数字相同的组合，所以答案应该再加上n。

3. 总的来说，如果A的因数个数a，B的因数个数b，那么由a*b是总结果，但是其中重复了D组，所以减去即可。但是如果正的来看 D+C+a*(b-C)+(a-C)*C 可以直接得出结果。

#include<cstdio>
#include<cstring>
int Gcd(int a,int b)
{
    int temp;
    while(b)
    {
        temp=a%b;
        a=b;
        b=temp;
    }
    return a;
}
int a[10000005];
int T;
int A,B,C,D;
int main()
{
    scanf("%d",&T);
    for(int i=1;i<=100000;i++)
        for(int j=1;i*j<=100000;j++)
            a[i*j]++;
    while(T--)
    {
        scanf("%d%d",&A,&B);
        C=a[Gcd(A,B)];
        D=C*(C-1)/2;
        printf("%d\n",a[A]*a[B]-D);
        //D+C+a[A]*(a[B]-C)+(a[A]-C)*C也是可以的。
    }
    return 0;
}

B：路径数量

题目描述

给出一个 n * n 的邻接矩阵A.

A是一个01矩阵 .

A[i][j]=1表示i号点和j号点之间有长度为1的边直接相连.

求出从 1 号点 到 n 号点长度为k的路径的数目.

输入描述:

第1行两个数n,k (20 ≤n ≤ 30,1 ≤ k ≤ 10)
第2行至第n+1行，为一个邻接矩阵

输出描述:

题目中所求的数目

输入

4 2
0 1 1 0
1 0 0 1
1 0 0 1
0 1 1 0

输出

2

说明

样例如图:
第一条路径：1-2-4
第二条路径：1-3-4

分析

1. 第一眼看到以为是深搜，但是n最大是30，而对于每一层，最多有30个方向，所以很有可能超时（只能过50%）
2. 如果要求 1~n 号的路径长度为K的路径个数，那我们可以换个方向想，由于路径是必须连续的，如果设dp[N][N] ,代表到达第j个点长度为k的路径数量。我们可以让路径长度k从1开始，递增到K，而对于每一个k，都由之前的 k-1 得出，最终可以得到·dp[n][k] 即为答案。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define MAX_N 3500
int N,K;
long long G[MAX_N][MAX_N];
long long dp[MAX_N][MAX_N];
int main(){
    scanf("%d%d",&N,&K);
    for(int i=1;i<=N;i++)
    {
        for(int j=1;j<=N;j++)
        {
            scanf("%lld",&G[i][j]);
        }
    }
    dp[1][0]=1;
    for(int k=1;k<=K;k++)
    {
        for(int i=1;i<=N;i++)
        {
            for(int j=1;j<=N;j++)
            {
                if(G[i][j])
                    dp[j][k]+=dp[i][k-1];
            }
        }
    }
    cout<<dp[N][K];
    return 0;
}

C：数列下标

题目描述

给出一个数列 A，求出一个数列B.

其中Bi 表示 数列A中 Ai 右边第一个比 Ai 大的数的下标(从1开始计数),没有找到这一个下标 Bi 就为0

输出数列B

输入描述:

第一行1个数字 n (n ≤ 10000)
第二行n个数字第 i 个数字为 Ai (0 ≤ Ai  ≤ 1000000000)

输出描述:

一共一行，第 i 个数和第 i+1 个数中间用空格隔开.

输入

6
3 2 6 1 1 2

输出

3 3 0 6 6 0

分析

没毛病直接暴力

int a[100001],b[100001];
int n;
int main()
{
    while(cin>>n)
    {
    	for(int i=1;i<=n;i++)
    	{
    		scanf("%d",&a[i]);
    	}
    	bool flag = 0;
    	for(int i=1;i<=n;i++)
    	{
    		flag = 0;
    		for(int j=i+1;j<=n;j++)
    		{
    			if(a[i]<a[j])
    			{
    				b[i] = j,flag = 1;
    				break;
    			}
    		}
    		if(!flag)
    			b[i] = 0;
    	}
    	printf("%d",b[1]);
    	for(int i=2;i<=n;i++)
    		printf(" %d",b[i]);
    	cout<<endl;
    }
    return 0;
}

D：星光晚餐

题目描述

Johnson和Nancy要在星光下吃晚餐。这是一件很浪漫的事情。

为了增加星光晚餐那浪漫的氛围，他拿出了一个神奇的魔法棒，并且可以按照一定的规则，改变天上星星的亮暗。

Johnson想考考Nancy，在他挥动魔法棒后，会有多少颗星星依旧闪耀在天空。他知道，Nancy一定会一口说出答案。

Nancy当然知道怎么做啦，但她想考考你！

Johnson先将天上n个星星排成一排，起初它们都是暗的。

他告诉他的妹子，他将挥动n次魔法棒，第i次挥动会将编号为i的正整数倍的星星的亮暗反转，即亮的星星转暗，暗的星星转亮。

Johnson想问Nancy，最终会有多少个星星依旧闪亮在天空。

输入描述:

一个整数n，含义请见题目描述。

输出描述:

一个整数ans，即n次操作后会有多少个星星依旧闪亮。

输入

3

输出

1

输入

7

输出

2

分析

1. 一个星星是否亮取决于它的因数个数是否为奇数。
2. 而一个数的因数个数是否为因数只取决于它是不是完全平方数。

long long ans;
long long n;
int main()
{
	while(cin>>n)
	{
	    cout<<(long long)sqrt(n)<<endl;
	}
    return 0;
}

E：括号序列

题目描述

给定括号长度N，给出一串括号（只包含小括号），计算出最少的交换（两两交换）次数，使整个括号序列匹配。 我们认为一个括号匹配，即对任意一个')'，在其左侧都有一个'('与它匹配，且他们形成一一映射关系。

输入描述:

第一行：整数N，表示括号序列长度
第二行：一个字符串，表示括号

输出描述:

一个整数，表示最少的交换次数

输入

复制

6
(()))(

输出

1

输入

6
)))(((

输出

2

分析

1. 贪心，对于每一个右括号，都要保证有一个左括号，所以用一个now来储存现在左括号的个数，如果now为0，就拿最右边的左括号来交换就ok。因为要时刻保存最右边的左括号的位置，可以用一个栈来储存。

#define MAX 5000005
char s[MAX];
int n;
stack<int> st;
int main()
{
    while(cin>>n)
    {
    	cin>>s;
    	while(!st.empty())
    		st.pop();
    	for(int i=0;i<n;i++)
    		if(s[i]=='(')st.push(i);
    	int now=0,ans = 0,index;
    	for(int i=0;i<n;i++)
    	{
    		if(s[i]=='(')now++;
    		else
    		{
    			if(now>0)now--;
    			else
    			{
    				now++;
    				ans++;
    				index = st.top();st.pop();
    				swap(s[i],s[index]);
    			}
    		}
    	}
    	cout<<ans<<endl;
    }
    return 0;
}

F：假的数字游戏

稍后呈上。