In Place Algorithm

本篇是in place algorithm的学习笔记。目前学习的是in place merge与in place martrix transposition这两个算法。

1.in place merge

论文链接：Practical in-place merging

论文讨论的是如何O(n)时间复杂度，O(1)空间复杂度合并两个相邻的有序数组。

b) 将sublist1与sublist2按sqrt(n)进行block划分, 余下的尾元素移到开头作为buffer( buffer size >= sqrt(n)，我们不关注buffer内的元素是否有序 )

c) 选择排序( O(sqrt(n)*sqrt(n)) ), 将各个block排序，使得各个block的末尾元素呈非下降序列。

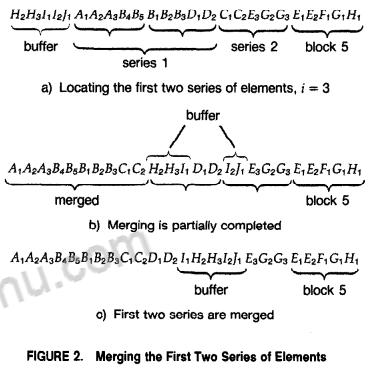
a) 找到首个block尾元素a[i]，使得a[i] > a[i+1]，显然之前的满足a[i] <= a[i+1]则之前的已成有序序列。划分好series1和series2.

b) c) 将series1与series2通过buffer进行merge, 直到series1内的元素全部排到正确位置，如c) 所示。

　　由于按段尾非下降排序各个block，显然series1会先于series2排完。

a) b) c) 将series2当作series1，series2的下一个block当作series2，重复之前的操作。以上操作的总的时间复杂度尾O(n).

d) sqrt(n) <= buffer size < 2*sqrt(n)， 冒泡排序/选择排序，将buffer变为有序序列，时间复杂度O(sqrt(n)*sqrt(n)).

附: 论文中，buffer中的元素是最大的，最后一步操作sort buffer内的元素，即可。

个人想法: 我们需要保证 buffer元素 >= 非buffer元素，否则我们仍然需要insert sort。因此，本人认为在merge前需要进行处理，从sublist1和sublist2中抠出前sqrt(n)大的元素，作为buffer。但这样可能会破坏block，导致某个block元素不够。个人认为可以抠多一点，再补回去。比如先扣除前 3*sqrt(n) 大的元素。这样补回到sublist1，至少还能余下sqrt(n)个元素。

总的时间复杂度为O(n). 可能常数略大。

2.in place matrix transposition

wiki: in place martrix transposition

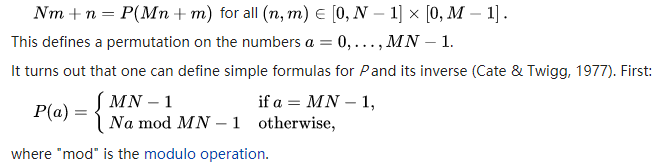
对于非方阵，进行置换操作。对于一个Circle，记录下初始节点，每次用前驱节点替换当前节点；用初始节点替换最后一个节点。

Non-square matrices: Following the cycles

for each length> cycle C of the permutation
    pick a starting address s in C
    let D = data at s
    let x = predecessor of s in the cycle
    while x ≠ s
        move data from x to successor of x
        let x = predecessor of x
    move data from D to successor of s

Improving memory locality at the cost of greater total data movement

reference to wiki