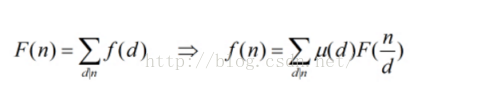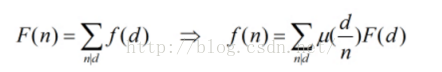HDU-1695 莫比乌斯反演
这里学习一下莫比乌斯反演
翻看了很多书,发现莫比乌斯反演,准确来说不是一种固有的公式,而是一种法则。
我们定义F(n),为f(d)的和函数,而定义f(n)为某儿算术函数。
反演公式1:反演n的因子时
废话不用多说,直接引入题目:
HDU-1695-GCD
给出a,b,c,d,k,
问[a,b]和[c,d]区间内部有多少不同的gcd(x,y)=k的对数目。
那么我们可以把GCD(x,y)进行分解。
由于某两个数的GCD是k,那么把这两个数除以K,那么这两个数的值,一定互质。那么我们可以这样。把区间变为[a/k,b/k],找到这个区间内部,GCD(X,Y)==1的对数。
怎么用好反演函数呢??
首先我们要把F(n)和f(d)的意义赋予好的定义。
这道题要求的是对数,那么求和函数F(d)为 有多少对(x,y)满足 gcd(x,y)== d 的倍数 。f(d)为有多少对(x,y)满足 gcd(x,y)== d 。
很明显,我们需要用
这样理解,F(n)代表gcd(x,y)==n的倍数的个数,它的值其实等于所有n的倍数d的gcd(x,y)==d组数的和。
这样我们就成功反演了。并且我们需要的是gcd(x,y)=1那么带入n=1,那么这个值就非常容易算了,我们
就只需要算当d=i时,他的F(i)是多少,这就是代码,这个区间内部,gcd(x,y)==k*i(意思是gcd(x,y)为i及其倍数的)个数,这个其实就非常简单了,n/i * m/i即可,意思是x在一个范围内所有i的倍数,乘以y能取到的所有i的倍数的个数相乘,就是答案,最后做和。不过题目忽略了(x,y)和(y,x)那么我们需要在相同区间的就是能取到(x,y)(y,x)的部分,重新计算这个值,然后除以2即可。
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define LL long long
using namespace std;
const int maxn = +;
const int INF = 0x3f3f3f3f;
int miu[maxn];
bool vis[maxn];
int prime[maxn];
int mu[maxn];
int a,b,c,d,k;
void init(){
int M=maxn;
memset(prime,,sizeof(prime));
memset(mu,,sizeof(mu));
memset(vis,,sizeof(vis));
mu[]=;
int cnt=;
for (int i=;i<maxn;i++){
if (!vis[i]){//质数
prime[cnt++]=i;
mu[i]=-;//质数的mobius为-1
}
for (int j=;j<cnt && i*prime[j]<maxn ;j++){
vis[i*prime[j]]=;//筛掉
if (i%prime[j])mu[i*prime[j]]=-mu[i];
else {
mu[i*prime[j]]=;
break;
}
}
}
}
int main(){
int t;
scanf("%d",&t);
int ca=;
init();
while(t--){
ca++;
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
if (k==){
printf("Case %d: 0\n",ca);
continue;
}
if (b>d)swap(b,d);
b=b/k;
d=d/k;
LL ans1=,ans2=;
for (int i=;i<=b;i++){
ans1+=(LL)mu[i]*(b/i)*(d/i);
}
for (int i=;i<=b;i++){
ans2+=(LL)mu[i]*(b/i)*(b/i);
}
printf("Case %d: %lld\n",ca,ans1-ans2/);
}
return ;
}
HDU-1695 莫比乌斯反演的更多相关文章
- HDU 1695 (莫比乌斯反演) GCD
题意: 从区间[1, b]和[1, d]中分别选一个x, y,使得gcd(x, y) = k, 求满足条件的xy的对数(不区分xy的顺序) 分析: 虽然之前写过一个莫比乌斯反演的总结,可遇到这道题还是 ...
- GCD HDU - 1695 莫比乌斯反演入门
题目链接:https://cn.vjudge.net/problem/HDU-1695#author=541607120101 感觉讲的很好的一个博客:https://www.cnblogs.com/ ...
- hdu 1695(莫比乌斯反演)
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- HDU 4746 (莫比乌斯反演) Mophues
这道题看巨巨的题解看了好久,好久.. 本文转自hdu4746(莫比乌斯反演) 题意:给出n, m, p,求有多少对a, b满足gcd(a, b)的素因子个数<=p,(其中1<=a<= ...
- HDU 5212 莫比乌斯反演
Code Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submis ...
- HDU 6053(莫比乌斯反演)
题意略. 思路:首先想到暴力去扫,这样的复杂度是n * min(ai),对于gcd = p,对答案的贡献应该是 (a1 / p) * (a2 / p) * .... * (an / p),得出这个贡献 ...
- hdu 4746Mophues[莫比乌斯反演]
Mophues Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 327670/327670 K (Java/Others) Total ...
- 算术 HDU - 6715 (莫比乌斯反演)
大意: 给定$n,m$, 求$\sum\limits_{i=1}^n\sum\limits_{j=1}^m\mu(lcm(i,j))$ 首先有$\mu(lcm(i,j))=\mu(i)\mu(j)\m ...
- HDU 4746 莫比乌斯反演+离线查询+树状数组
题目大意: 一个数字组成一堆素因子的乘积,如果一个数字的素因子个数(同样的素因子也要多次计数)小于等于P,那么就称这个数是P的幸运数 多次询问1<=x<=n,1<=y<=m,P ...
- HDU 5382 莫比乌斯反演
题目大意: 求S(n)的值 n<=1000000 这是官方题解给出的推导过程,orz,按这上面说的来写,就不难了 这里需要思考的就是G(n)这个如何利用积性函数的性质线性筛出来 作为一个质数,那 ...
随机推荐
- HDFS架构及原理
原文链接:HDFS架构及原理 引言 进入大数据时代,数据集的大小已经超过一台独立物理计算机的存储能力,我们需要对数据进行分区(partition)并存储到若干台单独的计算机上,也就出现了管理网络中跨多 ...
- Spring之BeanFactory和FactoryBean接口的区别
目录 一.BeanFactory接口 二.FactoryBean接口 1.简单实现 2.增强实现 3.FactoryBean的实际使用案例 三.总结 @ Spring框架中的BeanFactory ...
- 【20190129】CSS-垂直水平居中相关
元素居中是HTML和CSS永恒的问题,记录一下我使用的居中方法: 1. 块状元素水平居中,主要用于页面整体布局: margin: 0 auto; 2. 文字水平居中,适用于内联元素或inline- ...
- 微信小程序(二)登录授权实现
相对于上一节,这一节主要是动态获取数据,主要是对登陆信息的接收,以及页面获取授权按钮的相对相应(未授权时,显示,授权后不显示) 关键在于状态值的判断,以及对页面的不同响应(m-->v) wxml ...
- 使用synchronized的几种场景
1.修饰一个方法synchronized 修饰一个方法很简单,就是在方法的前面加synchronized,例如: public synchronized void method() { // todo ...
- 网上都没有提到的教程:python捕获异常后,怎么输出错误文件和行号
1.假设输出不存在的变量 a try: print(a) except NameError as e: print('发生错误的文件:', e.__traceback__.tb_frame.f_glo ...
- PYTHON常用数据类型(列表,元组,字典)
一.数字 1.整形:就是整数. 2.浮点型:就是小数. 3.布尔型:True或者是False,python里严格区分格式,空格缩进或者是大小写. 4.运算符有+ – * / ()%(求模运算取余数)* ...
- 关于swagger——WebApi一个controller中出现多个Get是出现错误的处理
如 /// <summary> /// 测试处理 /// </summary> public class TestController : ApiController { // ...
- Apollo的Oracle适配改动
这几天工作需要使用Apollo配置中心.Apollo唯一的依赖是MySQL数据库,然而公司只有Oracle数据库资源.这里有一个Oracle适配改动的分支,但是它是基于0.8.0版本的Apollo.看 ...
- Checkpoint 和Breakpoint
参考:http://www.cnblogs.com/qiangshu/p/5241699.htmlhttp://www.cnblogs.com/biwork/p/3366724.html 1. Che ...