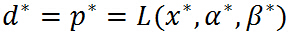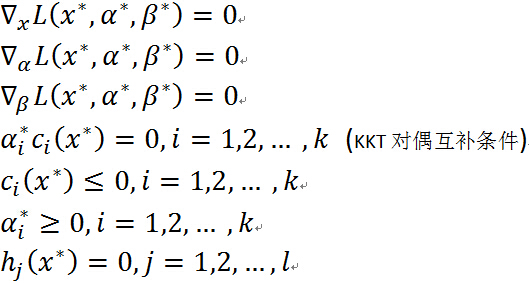简易解说拉格朗日对偶(Lagrange duality)
引言:尝试用最简单易懂的描述解释清楚机器学习中会用到的拉格朗日对偶性知识,非科班出身,如有数学专业博友,望多提意见!
1.原始问题
假设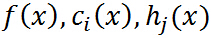 是定义在
是定义在 上的连续可微函数(为什么要求连续可微呢,后面再说,这里不用多想),考虑约束最优化问题:
上的连续可微函数(为什么要求连续可微呢,后面再说,这里不用多想),考虑约束最优化问题:
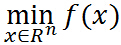
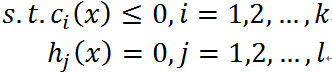
称为约束最优化问题的原始问题。
现在如果不考虑约束条件,原始问题就是:
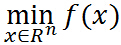
因为假设其连续可微,利用高中的知识,对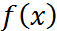 求导数,然后令导数为0,就可解出最优解,很easy. 那么,问题来了(呵呵。。。),偏偏有约束条件,好烦啊,要是能想办法把约束条件去掉就好了,bingo! 拉格朗日函数就是干这个的。
求导数,然后令导数为0,就可解出最优解,很easy. 那么,问题来了(呵呵。。。),偏偏有约束条件,好烦啊,要是能想办法把约束条件去掉就好了,bingo! 拉格朗日函数就是干这个的。
引进广义拉格朗日函数(generalized Lagrange function):
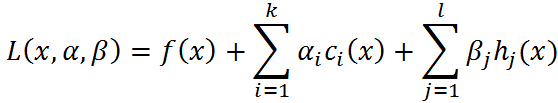
不要怕这个式子,也不要被拉格朗日这个高大上的名字给唬住了,让我们慢慢剖析!这里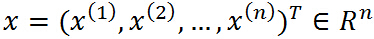 ,
, 是拉格朗日乘子(名字高大上,其实就是上面函数中的参数而已),特别要求
是拉格朗日乘子(名字高大上,其实就是上面函数中的参数而已),特别要求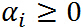 .
.
现在,如果把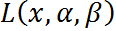 看作是关于
看作是关于 的函数,要求其最大值,即
的函数,要求其最大值,即
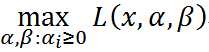
再次注意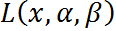 是一个关于
是一个关于 的函数,经过我们优化(不要管什么方法),就是确定
的函数,经过我们优化(不要管什么方法),就是确定 的值使得
的值使得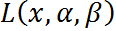 取得最大值(此过程中把
取得最大值(此过程中把 看做常量),确定了
看做常量),确定了 的值,就可以得到
的值,就可以得到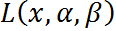 的最大值,因为
的最大值,因为 已经确定,显然最大值
已经确定,显然最大值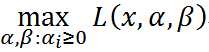 就是只和
就是只和 有关的函数,定义这个函数为:
有关的函数,定义这个函数为:
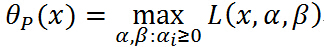
其中 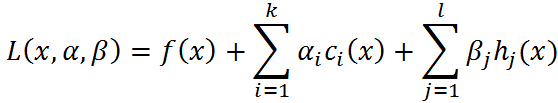
下面通过 是否满足约束条件两方面来分析这个函数:
是否满足约束条件两方面来分析这个函数:
- 考虑某个
 违反了原始的约束,即
违反了原始的约束,即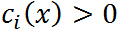 或者
或者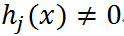 ,那么:
,那么:
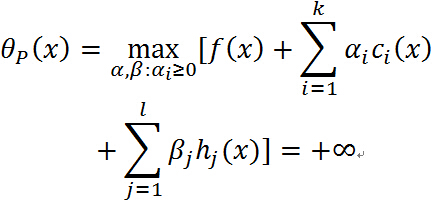
注意中间的最大化式子就是确定 的之后的结果,若
的之后的结果,若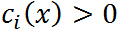 ,则令
,则令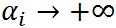 ,如果
,如果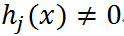 ,很容易取值
,很容易取值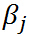 使得
使得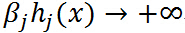
- 考虑
 满足原始的约束,则:
满足原始的约束,则: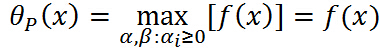 ,注意中间的最大化是确定
,注意中间的最大化是确定 的过程,
的过程,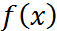 就是个常量,常量的最大值显然是本身.
就是个常量,常量的最大值显然是本身.
通过上面两条分析可以得出:

那么在满足约束条件下:
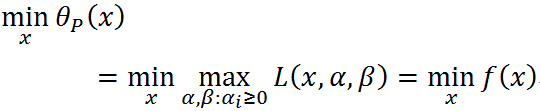
即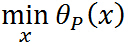 与原始优化问题等价,所以常用
与原始优化问题等价,所以常用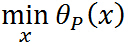 代表原始问题,下标 P 表示原始问题,定义原始问题的最优值:
代表原始问题,下标 P 表示原始问题,定义原始问题的最优值:
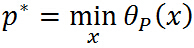
原始问题讨论就到这里,做一个总结:通过拉格朗日这位大神的办法重新定义一个无约束问题(大家都喜欢无拘无束),这个无约束问题等价于原来的约束优化问题,从而将约束问题无约束化!
2.对偶问题
定义关于 的函数:
的函数:
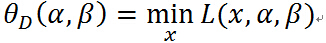
注意等式右边是关于 的函数的最小化,
的函数的最小化, 确定以后,最小值就只与
确定以后,最小值就只与 有关,所以是一个关于
有关,所以是一个关于 的函数.
的函数.
考虑极大化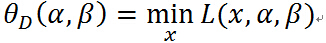 ,即
,即
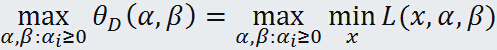
这就是原始问题的对偶问题,再把原始问题写出来:
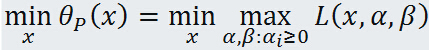
形式上可以看出很对称,只不过原始问题是先固定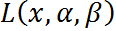 中的
中的 ,优化出参数
,优化出参数 ,再优化最优
,再优化最优 ,而对偶问题是先固定
,而对偶问题是先固定 ,优化出最优
,优化出最优 ,然后再确定参数
,然后再确定参数 .
.
定义对偶问题的最优值:
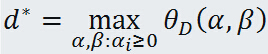
3. 原始问题与对偶问题的关系
定理:若原始问题与对偶问题都有最优值,则
证明:对任意的 和
和 ,有
,有
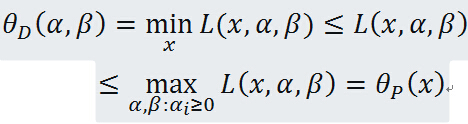
即

由于原始问题与对偶问题都有最优值,所以
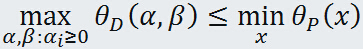
即
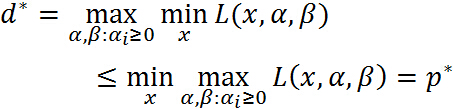
也就是说原始问题的最优值不小于对偶问题的最优值,但是我们要通过对偶问题来求解原始问题,就必须使得原始问题的最优值与对偶问题的最优值相等,于是可以得出下面的推论:
推论:设
分别是原始问题和对偶问题的可行解,如果
,那么
分别是原始问题和对偶问题的最优解。
所以,当原始问题和对偶问题的最优值相等: 时,可以用求解对偶问题来求解原始问题(当然是对偶问题求解比直接求解原始问题简单的情况下),但是到底满足什么样的条件才能使的
时,可以用求解对偶问题来求解原始问题(当然是对偶问题求解比直接求解原始问题简单的情况下),但是到底满足什么样的条件才能使的 呢,这就是下面要阐述的 KKT 条件
呢,这就是下面要阐述的 KKT 条件
4. KKT 条件
定理:对于原始问题和对偶问题,假设函数
和
是凸函数,
是仿射函数(即由一阶多项式构成的函数,f(x)=Ax + b, A是矩阵,x,b是向量);并且假设不等式约束
是严格可行的,即存在
,对所有
有
,则存在
,使得
是原始问题的最优解,
是对偶问题的最优解,并且
定理:对于原始问题和对偶问题,假设函数
和
是凸函数,
是仿射函数(即由一阶多项式构成的函数,f(x)=Ax + b, A是矩阵,x,b是向量);并且假设不等式约束
是严格可行的,即存在
,对所有
有
,则
分别是原始问题和对偶问题的最优解的充分必要条件是
满足下面的Karush-Kuhn-Tucker(KKT)条件:
关于KKT 条件的理解:前面三个条件是由解析函数的知识,对于各个变量的偏导数为0(这就解释了一开始为什么假设三个函数连续可微,如果不连续可微的话,这里的偏导数存不存在就不能保证),后面四个条件就是原始问题的约束条件以及拉格朗日乘子需要满足的约束。
特别注意当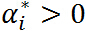 时,由KKT对偶互补条件可知:
时,由KKT对偶互补条件可知: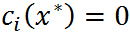 ,这个知识点会在 SVM 的推导中用到.
,这个知识点会在 SVM 的推导中用到.
5. 总结
一句话,某些条件下,把原始的约束问题通过拉格朗日函数转化为无约束问题,如果原始问题求解棘手,在满足KKT的条件下用求解对偶问题来代替求解原始问题,使得问题求解更加容易。
简易解说拉格朗日对偶(Lagrange duality)的更多相关文章
- 简易解说拉格朗日对偶(Lagrange duality)(转载)
引言:尝试用最简单易懂的描述解释清楚机器学习中会用到的拉格朗日对偶性知识,非科班出身,如有数学专业博友,望多提意见! 1.原始问题 假设是定义在上的连续可微函数(为什么要求连续可微呢,后面再说,这里不 ...
- 简易解说拉格朗日对偶(Lagrange duality)(转载)
转载自https://www.cnblogs.com/90zeng/p/Lagrange_duality.html,本人觉得讲的非常好! 1.原始问题 假设是定义在上的连续可微函数(为什么要求连续可微 ...
- 拉格朗日对偶性(Lagrange duality)
目录 拉格朗日对偶性(Lagrange duality) 1. 从原始问题到对偶问题 2. 弱对偶与强对偶 3. KKT条件 Reference: 拉格朗日对偶性(Lagrange duality) ...
- SVM小白教程(2):拉格朗日对偶
在上一篇文章中,我们推导出了 SVM 的目标函数: \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \\ \operat ...
- Support Vector Machine(2):Lagrange Duality求解线性可分SVM的最佳边界
在上篇文章<Support Vector Machine(1):线性可分集的决策边界>中,我们最后得到,求SVM最佳Margin的问题,转化为了如下形式: 到这一步后,我个人又花了很长的时 ...
- 拉格朗日对偶(Lagrange duality)
拉格朗日对偶(Lagrange duality) 存在等式约束的极值问题求法,比如下面的最优化问题: 目标函数是f(w),下面是等式约束.通常解法是引入拉格朗日算子,这里使用 ...
- SVM(支持向量机)(二)—Lagrange Duality(拉格朗日对偶问题)
(整理自AndrewNG的课件,转载请注明.整理者:华科小涛@http://www.cnblogs.com/hust-ghtao/) SVM有点让人头疼,但还是要弄明白.把这一大块搞懂了,会很有成就感 ...
- 3. SVM分类器求解(1)——Lagrange duality
先抛开上面的二次规划问题,先来看看存在等式约束的极值问题求法,比如下面的最优化问题: 目标函数是f(w),下面是等式约束.通常解法是引入拉格朗日算子,这里使用来表示算子,得到拉格朗日公式为 是等式约束 ...
- 拉格朗日(Lagrange)插值算法
拉格朗日插值(Lagrange interpolation)是一种多项式插值方法,指插值条件中不出现被插函数导数值,过n+1个样点,满足如下图的插值条件的多项式.也叫做拉格朗日公式. 这里以拉格朗日 ...
随机推荐
- 外部访问docker中的MySQL
注:192.168.1.203机器上装有docker,容器在该机器上 mysql> use mysql; mysql> update user set authentication_str ...
- 【P2015】二叉苹果树 (树形DP分组背包)
题目描述 有一棵苹果树,如果树枝有分叉,一定是分2叉(就是说没有只有1个儿子的结点) 这棵树共有N个结点(叶子点或者树枝分叉点),编号为1-N,树根编号一定是1. 现在这颗树枝条太多了,需要剪枝.但是 ...
- P1273 有线电视网
题目描述 某收费有线电视网计划转播一场重要的足球比赛.他们的转播网和用户终端构成一棵树状结构,这棵树的根结点位于足球比赛的现场,树叶为各个用户终端,其他中转站为该树的内部节点. 从转播站到转播站以及从 ...
- ELK原理与简介
为什么用到ELK: 一般我们需要进行日志分析场景:直接在日志文件中 grep.awk 就可以获得自己想要的信息.但在规模较大的场景中,此方法效率低下,面临问题包括日志量太大如何归档.文本搜索太慢怎么办 ...
- 小小知识点(四)——MATLAB如何画等高线图和线性规划约束方程
MATLAB程序: figure contourf(x,y,data) % 画等高线 hold on plot(x,y(x)) %画线性规划约束方程1 hold on plot(y,x(y)) %画线 ...
- 【学习总结】GirlsInAI ML-diary day-14-function函数
[学习总结]GirlsInAI ML-diary 总 原博github链接-day14 认识函数function 函数相当于一个固定的公式,一个映射.有输入,有输出. 1-python内置函数 max ...
- jexus部署webapi或mvc报错处理
1路径错误:因为Windows和Linux的路径问题大小写问题. 解决: 修改jexus下的jws把export MONO_IOMAP=all注释去掉放出来. 2, 解决: 卸载
- adoop(四)HDFS集群详解
阅读目录(Content) 一.HDFS概述 1.1.HDFS概述 1.2.HDFS的概念和特性 1.3.HDFS的局限性 1.4.HDFS保证可靠性的措施 二.HDFS基本概念 2.1.HDFS主从 ...
- Zabbix 3.0的前端默认在Centos 6上不支持
由于PHP版本的原因,RHEL 6上的Zabbix前端不受支持. 由于Zabbix 3.0的要求是PHP 5.4.0或更高版本,而RHEL 6最新版本是5.3.3. 在大多数情况下,Zabbix服务器 ...
- spring cloud实战与思考(三) 微服务之间通过fiegn上传一组文件(下)
需求场景: 用户调用微服务1的接口上传一组图片和对应的描述信息.微服务1处理后,再将这组图片上传给微服务2进行处理.各个微服务能区分开不同的图片进行不同处理. 上一篇博客已经讨论了在微服务之间传递一组 ...