Sequence Models Week 1 Character level language model - Dinosaurus land
Character level language model - Dinosaurus land
Welcome to Dinosaurus Island! 65 million years ago, dinosaurs existed, and in this assignment they are back. You are in charge of a special task. Leading biology researchers are creating new breeds of dinosaurs and bringing them to life on earth, and your job is to give names to these dinosaurs. If a dinosaur does not like its name, it might go berserk, so choose wisely!

By completing this assignment you will learn:Luckily you have learned some deep learning and you will use it to save the day. Your assistant has collected a list of all the dinosaur names they could find, and compiled them into this dataset. (Feel free to take a look by clicking the previous link.) To create new dinosaur names, you will build a character level language model to generate new names. Your algorithm will learn the different name patterns, and randomly generate new names. Hopefully this algorithm will keep you and your team safe from the dinosaurs' wrath!
- How to store text data for processing using an RNN
- How to synthesize data, by sampling predictions at each time step and passing it to the next RNN-cell unit
- How to build a character-level text generation recurrent neural network
- Why clipping the gradients is important
We will begin by loading in some functions that we have provided for you in rnn_utils. Specifically, you have access to functions such as rnn_forward and rnn_backward which are equivalent to those you've implemented in the previous assignment.
import numpy as np
from utils import *
import random
1.1 - Dataset and Preprocessing
Run the following cell to read the dataset of dinosaur names, create a list of unique characters (such as a-z), and compute the dataset and vocabulary size.
data = open('dinos.txt', 'r').read()
data= data.lower()
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))
There are 19909 total characters and 27 unique characters in your data.
The characters are a-z (26 characters) plus the "\n" (or newline character), which in this assignment plays a role similar to the <EOS> (or "End of sentence") token we had discussed in lecture, only here it indicates the end of the dinosaur name rather than the end of a sentence. In the cell below, we create a python dictionary (i.e., a hash table) to map each character to an index from 0-26. We also create a second python dictionary that maps each index back to the corresponding character character. This will help you figure out what index corresponds to what character in the probability distribution output of the softmax layer. Below, char_to_ix and ix_to_char are the python dictionaries.
char_to_ix = { ch:i for i,ch in enumerate(sorted(chars)) }
ix_to_char = { i:ch for i,ch in enumerate(sorted(chars)) }
print(ix_to_char)
{0: '\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}
1.2 - Overview of the model
Your model will have the following structure:
- Initialize parameters
- Run the optimization loop
- Forward propagation to compute the loss function
- Backward propagation to compute the gradients with respect to the loss function
- Clip the gradients to avoid exploding gradients
- Using the gradients, update your parameter with the gradient descent update rule.
- Return the learned parameters

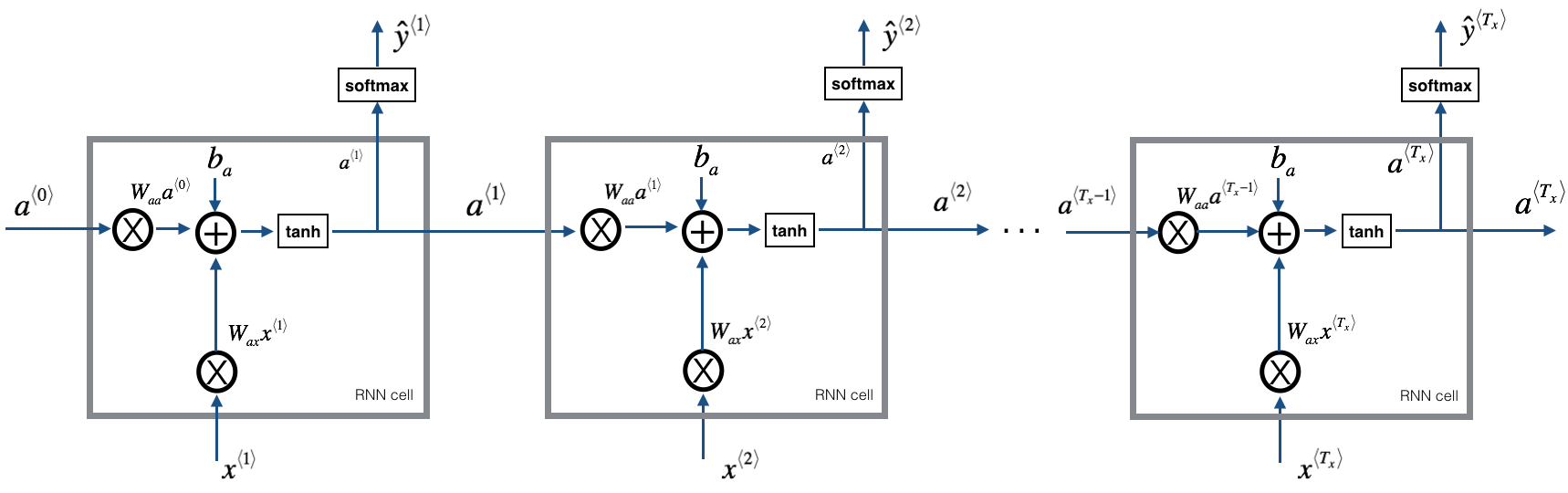
Figure 1: Recurrent Neural Network, similar to what you had built in the previous notebook "Building a RNN - Step by Step".
At each time-step, the RNN tries to predict what is the next character given the previous characters. The dataset X=(x⟨1⟩,x⟨2⟩,...,x⟨Tx⟩)X=(x⟨1⟩,x⟨2⟩,...,x⟨Tx⟩) is a list of characters in the training set, while Y=(y⟨1⟩,y⟨2⟩,...,y⟨Tx⟩)Y=(y⟨1⟩,y⟨2⟩,...,y⟨Tx⟩) is such that at every time-step tt, we have y⟨t⟩=x⟨t+1⟩y⟨t⟩=x⟨t+1⟩.
2 - Building blocks of the model
In this part, you will build two important blocks of the overall model:
- Gradient clipping: to avoid exploding gradients
- Sampling: a technique used to generate characters
You will then apply these two functions to build the model.
2.1 - Clipping the gradients in the optimization loop
In this section you will implement the clip function that you will call inside of your optimization loop. Recall that your overall loop structure usually consists of a forward pass, a cost computation, a backward pass, and a parameter update. Before updating the parameters, you will perform gradient clipping when needed to make sure that your gradients are not "exploding," meaning taking on overly large values.
In the exercise below, you will implement a function clip that takes in a dictionary of gradients and returns a clipped version of gradients if needed. There are different ways to clip gradients; we will use a simple element-wise clipping procedure, in which every element of the gradient vector is clipped to lie between some range [-N, N]. More generally, you will provide a maxValue (say 10). In this example, if any component of the gradient vector is greater than 10, it would be set to 10; and if any component of the gradient vector is less than -10, it would be set to -10. If it is between -10 and 10, it is left alone.
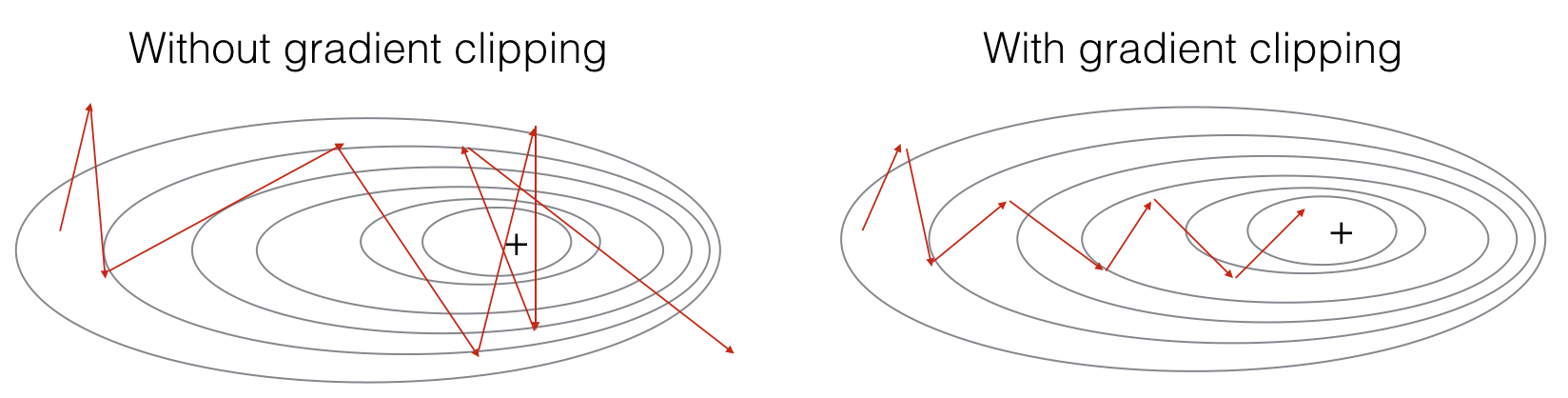

Figure 2: Visualization of gradient descent with and without gradient clipping, in a case where the network is running into slight "exploding gradient" problems.
Exercise: Implement the function below to return the clipped gradients of your dictionary gradients. Your function takes in a maximum threshold and returns the clipped versions of your gradients. You can check out this hint for examples of how to clip in numpy. You will need to use the argument out = ....
### GRADED FUNCTION: clip
def clip(gradients, maxValue):
'''
Clips the gradients' values between minimum and maximum.
Arguments:
gradients -- a dictionary containing the gradients "dWaa", "dWax", "dWya", "db", "dby"
maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue
Returns:
gradients -- a dictionary with the clipped gradients.
''' dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby'] ### START CODE HERE ###
# clip to mitigate exploding gradients, loop over [dWax, dWaa, dWya, db, dby]. (≈2 lines)
for gradient in [dWax, dWaa, dWya, db, dby]:
np.clip(gradient, -maxValue, maxValue, out=gradient)
### END CODE HERE ### gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby} return gradients
np.random.seed(3)
dWax = np.random.randn(5,3)*10
dWaa = np.random.randn(5,5)*10
dWya = np.random.randn(2,5)*10
db = np.random.randn(5,1)*10
dby = np.random.randn(2,1)*10
gradients = {"dWax": dWax, "dWaa": dWaa, "dWya": dWya, "db": db, "dby": dby}
gradients = clip(gradients, 10)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
gradients["dWaa"][1][2] = 10.0
gradients["dWax"][3][1] = -10.0
gradients["dWya"][1][2] = 0.29713815361
gradients["db"][4] = [ 10.]
gradients["dby"][1] = [ 8.45833407]
Expected output:
| gradients["dWaa"][1][2] | 10.0 |
| gradients["dWax"][3][1] | -10.0 |
| gradients["dWya"][1][2] | 0.29713815361 |
| gradients["db"][4] | [ 10.] |
| gradients["dby"][1] | [ 8.45833407] |
2.2 - Sampling
Now assume that your model is trained. You would like to generate new text (characters). The process of generation is explained in the picture below:
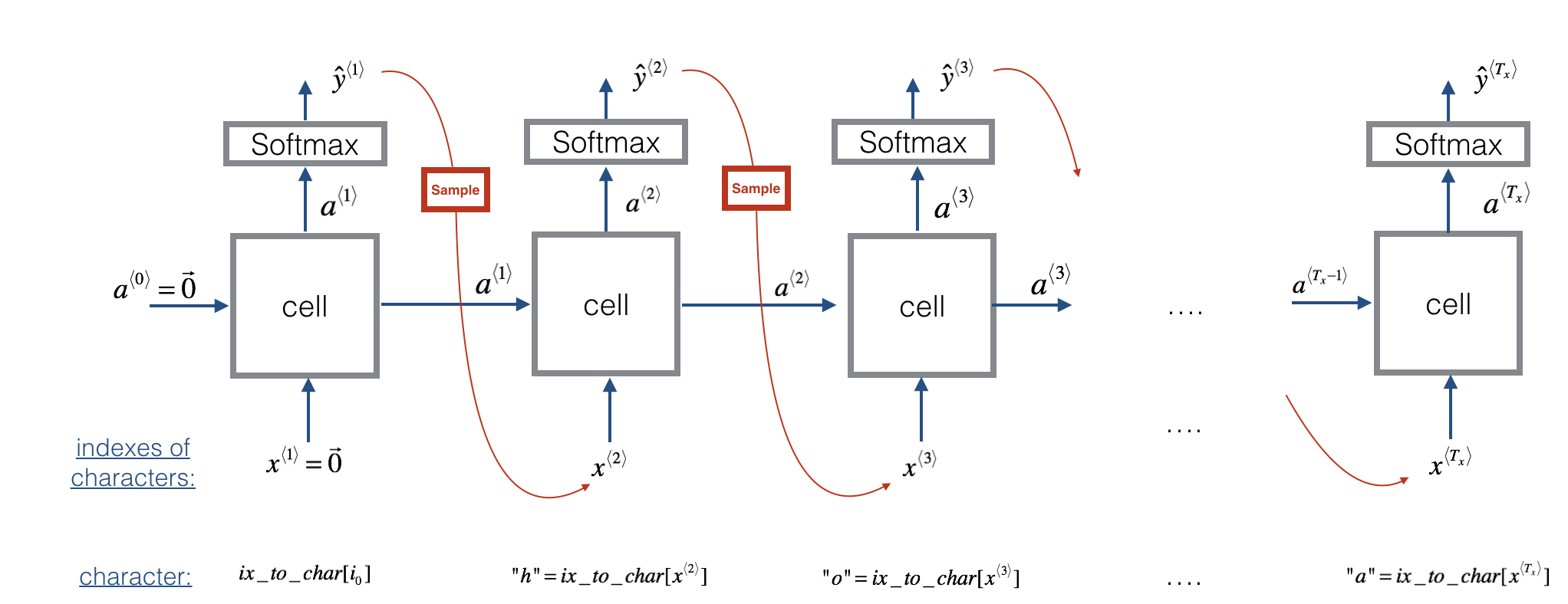

Figure 3: In this picture, we assume the model is already trained. We pass in x⟨1⟩=0⃗ x⟨1⟩=0→ at the first time step, and have the network then sample one character at a time.
Exercise: Implement the sample function below to sample characters. You need to carry out 4 steps:
Step 1: Pass the network the first "dummy" input x⟨1⟩=0⃗ x⟨1⟩=0→ (the vector of zeros). This is the default input before we've generated any characters. We also set a⟨0⟩=0⃗
Step 2: Run one step of forward propagation to get a⟨1⟩a⟨1⟩ and ŷ ⟨1⟩y^⟨1⟩. Here are the equations:
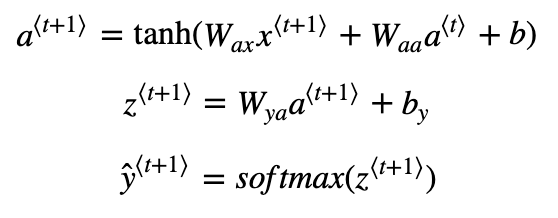
Note that ŷ ⟨t+1⟩y^⟨t+1⟩ is a (softmax) probability vector (its entries are between 0 and 1 and sum to 1). ŷ ⟨t+1⟩iy^i⟨t+1⟩ represents the probability that the character indexed by "i" is the next character. We have provided a softmax() function that you can use.
- Step 3: Carry out sampling: Pick the next character's index according to the probability distribution specified by ŷ ⟨t+1⟩y^⟨t+1⟩. This means that if ŷ ⟨t+1⟩i=0.16y^i⟨t+1⟩=0.16, you will pick the index "i" with 16% probability. To implement it, you can use
np.random.choice.
Here is an example of how to use np.random.choice():
np.random.seed(0)
p = np.array([0.1, 0.0, 0.7, 0.2])
index = np.random.choice([0, 1, 2, 3], p = p.ravel())
This means that you will pick the index according to the distribution: P(index=0)=0.1,P(index=1)=0.0,P(index=2)=0.7,P(index=3)=0.2P(index=0)=0.1,P(index=1)=0.0,P(index=2)=0.7,P(index=3)=0.2.
- Step 4: The last step to implement in
sample()is to overwrite the variablex, which currently stores x⟨t⟩x⟨t⟩, with the value of x⟨t+1⟩x⟨t+1⟩. You will represent x⟨t+1⟩x⟨t+1⟩by creating a one-hot vector corresponding to the character you've chosen as your prediction. You will then forward propagate x⟨t+1⟩x⟨t+1⟩ in Step 1 and keep repeating the process until you get a "\n" character, indicating you've reached the end of the dinosaur name.
# GRADED FUNCTION: sample
def sample(parameters, char_to_ix, seed):
"""
Sample a sequence of characters according to a sequence of probability distributions output of the RNN
Arguments:
parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b.
char_to_ix -- python dictionary mapping each character to an index.
seed -- used for grading purposes. Do not worry about it.
Returns:
indices -- a list of length n containing the indices of the sampled characters.
""" # Retrieve parameters and relevant shapes from "parameters" dictionary
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
vocab_size = by.shape[0]
n_a = Waa.shape[1] ### START CODE HERE ###
# Step 1: Create the one-hot vector x for the first character (initializing the sequence generation). (≈1 line)
x = np.zeros((vocab_size,1)) #自己没想到
# Step 1': Initialize a_prev as zeros (≈1 line)
a_prev = np.zeros((n_a,1)) # Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)
indices = [] # Idx is a flag to detect a newline character, we initialize it to -1
idx = -1 # Loop over time-steps t. At each time-step, sample a character from a probability distribution and append
# its index to "indices". We'll stop if we reach 50 characters (which should be very unlikely with a well
# trained model), which helps debugging and prevents entering an infinite loop.
counter = 0
newline_character = char_to_ix['\n'] while (idx != newline_character and counter != 50): # Step 2: Forward propagate x using the equations (1), (2) and (3)
a = np.tanh(np.dot(Wax,x)+np.dot(Waa,a_prev)+b)
z = np.dot(Wya,a)+by
y = softmax(z) # for grading purposes
np.random.seed(counter+seed) # Step 3: Sample the index of a character within the vocabulary from the probability distribution y
idx = np.random.choice(range(vocab_size), p = y.ravel())
# Append the index to "indices"
indices.append(idx) # Step 4: Overwrite the input character as the one corresponding to the sampled index.
x = np.zeros((vocab_size,1)) #这一行不能少,因为每一轮结束后x都要重新赋值,和前面初始化x的代码并不重复
#前面是令x<0>=0,这里是每一轮结束后x都要重写,两者功能不同
x[idx] = 1 # Update "a_prev" to be "a"
a_prev = a # for grading purposes
seed += 1
counter +=1 ### END CODE HERE ###
if (counter == 50):
indices.append(char_to_ix['\n']) return indices
np.random.seed(2)
_, n_a = 20, 100
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
indices = sample(parameters, char_to_ix, 0)
print("Sampling:")
print("list of sampled indices:", indices)
print("list of sampled characters:", [ix_to_char[i] for i in indices])
Sampling:
list of sampled indices: [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 17, 24, 12, 13, 24, 0]
list of sampled characters: ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'q', 'x', 'l', 'm', 'x', '\n']
Expected output:
| list of sampled indices: | [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 5, 6, 12, 25, 0, 0] |
| list of sampled characters: | ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'e', 'f', 'l', 'y', '\n', '\n'] |
3 - Building the language model
It is time to build the character-level language model for text generation.
3.1 - Gradient descent
In this section you will implement a function performing one step of stochastic gradient descent (with clipped gradients). You will go through the training examples one at a time, so the optimization algorithm will be stochastic gradient descent. As a reminder, here are the steps of a common optimization loop for an RNN:
- Forward propagate through the RNN to compute the loss
- Backward propagate through time to compute the gradients of the loss with respect to the parameters
- Clip the gradients if necessary
- Update your parameters using gradient descent
Exercise: Implement this optimization process (one step of stochastic gradient descent).
We provide you with the following functions:
def rnn_forward(X, Y, a_prev, parameters):
""" Performs the forward propagation through the RNN and computes the cross-entropy loss.
It returns the loss' value as well as a "cache" storing values to be used in the backpropagation."""
....
return loss, cache
def rnn_backward(X, Y, parameters, cache):
""" Performs the backward propagation through time to compute the gradients of the loss with respect
to the parameters. It returns also all the hidden states."""
...
return gradients, a
def update_parameters(parameters, gradients, learning_rate):
""" Updates parameters using the Gradient Descent Update Rule."""
...
return parameters
# GRADED FUNCTION: optimize
def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
"""
Execute one step of the optimization to train the model.
Arguments:
X -- list of integers, where each integer is a number that maps to a character in the vocabulary.
Y -- list of integers, exactly the same as X but shifted one index to the left.
a_prev -- previous hidden state.
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
b -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
learning_rate -- learning rate for the model.
Returns:
loss -- value of the loss function (cross-entropy)
gradients -- python dictionary containing:
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
db -- Gradients of bias vector, of shape (n_a, 1)
dby -- Gradients of output bias vector, of shape (n_y, 1)
a[len(X)-1] -- the last hidden state, of shape (n_a, 1)
""" ### START CODE HERE ### # Forward propagate through time (≈1 line)
loss, cache = rnn_forward(X, Y, a_prev, parameters) # Backpropagate through time (≈1 line)
gradients, a = rnn_backward(X, Y, parameters, cache) # Clip your gradients between -5 (min) and 5 (max) (≈1 line)
gradients = clip(gradients, 5) # Update parameters (≈1 line)
parameters = update_parameters(parameters, gradients, learning_rate) ### END CODE HERE ### return loss, gradients, a[len(X)-1]
np.random.seed(1)
vocab_size, n_a = 27, 100
a_prev = np.random.randn(n_a, 1)
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
X = [12,3,5,11,22,3]
Y = [4,14,11,22,25, 26]
loss, gradients, a_last = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
print("Loss =", loss)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("np.argmax(gradients[\"dWax\"]) =", np.argmax(gradients["dWax"]))
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
print("a_last[4] =", a_last[4])
Loss = 126.503975722
gradients["dWaa"][1][2] = 0.194709315347
np.argmax(gradients["dWax"]) = 93
gradients["dWya"][1][2] = -0.007773876032
gradients["db"][4] = [-0.06809825]
gradients["dby"][1] = [ 0.01538192]
a_last[4] = [-1.]
Expected output:
| Loss | 126.503975722 |
| gradients["dWaa"][1][2] | 0.194709315347 |
| np.argmax(gradients["dWax"]) | 93 |
| gradients["dWya"][1][2] | -0.007773876032 |
| gradients["db"][4] | [-0.06809825] |
| gradients["dby"][1] | [ 0.01538192] |
| a_last[4] | [-1.] |
3.2 - Training the model
Given the dataset of dinosaur names, we use each line of the dataset (one name) as one training example. Every 100 steps of stochastic gradient descent, you will sample 10 randomly chosen names to see how the algorithm is doing. Remember to shuffle the dataset, so that stochastic gradient descent visits the examples in random order.
Exercise: Follow the instructions and implement model(). When examples[index] contains one dinosaur name (string), to create an example (X, Y), you can use this:
index = j % len(examples)
X = [None] + [char_to_ix[ch] for ch in examples[index]]
Y = X[1:] + [char_to_ix["\n"]]
Note that we use: index= j % len(examples), where j = 1....num_iterations, to make sure that examples[index] is always a valid statement (index is smaller than len(examples)). The first entry of X being None will be interpreted by rnn_forward() as setting x⟨0⟩=0⃗ x⟨0⟩=0→. Further, this ensures that Y is equal to X but shifted one step to the left, and with an additional "\n" appended to signify the end of the dinosaur name.
# GRADED FUNCTION: model
def model(data, ix_to_char, char_to_ix, num_iterations = 35000, n_a = 50, dino_names = 7, vocab_size = 27):
"""
Trains the model and generates dinosaur names.
Arguments:
data -- text corpus
ix_to_char -- dictionary that maps the index to a character
char_to_ix -- dictionary that maps a character to an index
num_iterations -- number of iterations to train the model for
n_a -- number of units of the RNN cell
dino_names -- number of dinosaur names you want to sample at each iteration.
vocab_size -- number of unique characters found in the text, size of the vocabulary
Returns:
parameters -- learned parameters
""" # Retrieve n_x and n_y from vocab_size
n_x, n_y = vocab_size, vocab_size # Initialize parameters
parameters = initialize_parameters(n_a, n_x, n_y) # Initialize loss (this is required because we want to smooth our loss, don't worry about it)
loss = get_initial_loss(vocab_size, dino_names) # Build list of all dinosaur names (training examples).
with open("dinos.txt") as f:
examples = f.readlines()
examples = [x.lower().strip() for x in examples] # Shuffle list of all dinosaur names
np.random.seed(0)
np.random.shuffle(examples) # Initialize the hidden state of your LSTM
a_prev = np.zeros((n_a, 1)) # Optimization loop
for j in range(num_iterations): ### START CODE HERE ### # Use the hint above to define one training example (X,Y) (≈ 2 lines)
#为什么下面的X,Y是这样的呢?是因为X<t+1>=Y<t>,且X<0>=0,
#反应在数组上就是下面的写法,Y相当于X向左移一位,这样Y<0>=X<1>,且Y<t>="\n"
index = j % len(examples)
X = [None] + [char_to_ix[ch] for ch in examples[index]]
Y = X[1:] + [char_to_ix["\n"]] # Perform one optimization step: Forward-prop -> Backward-prop -> Clip -> Update parameters
# Choose a learning rate of 0.01
curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate = 0.01) ### END CODE HERE ### # Use a latency trick to keep the loss smooth. It happens here to accelerate the training.
loss = smooth(loss, curr_loss)
# Every 2000 Iteration, generate "n" characters thanks to sample() to check if the model is learning properly
if j % 2000 == 0: print('Iteration: %d, Loss: %f' % (j, loss) + '\n') # The number of dinosaur names to print
seed = 0
for name in range(dino_names): # Sample indices and print them
sampled_indices = sample(parameters, char_to_ix, seed)
print_sample(sampled_indices, ix_to_char) seed += 1 # To get the same result for grading purposed, increment the seed by one. print('\n') return parameters
Run the following cell, you should observe your model outputting random-looking characters at the first iteration. After a few thousand iterations, your model should learn to generate reasonable-looking names.
parameters = model(data, ix_to_char, char_to_ix)
Iteration: 0, Loss: 23.087336 Nkzxwtdmfqoeyhsqwasjkjvu
Kneb
Kzxwtdmfqoeyhsqwasjkjvu
Neb
Zxwtdmfqoeyhsqwasjkjvu
Eb
Xwtdmfqoeyhsqwasjkjvu Iteration: 2000, Loss: 27.884160 Liusskeomnolxeros
Hmdaairus
Hytroligoraurus
Lecalosapaus
Xusicikoraurus
Abalpsamantisaurus
Tpraneronxeros Iteration: 4000, Loss: 25.901815 Mivrosaurus
Inee
Ivtroplisaurus
Mbaaisaurus
Wusichisaurus
Cabaselachus
Toraperlethosdarenitochusthiamamumamaon Iteration: 6000, Loss: 24.608779 Onwusceomosaurus
Lieeaerosaurus
Lxussaurus
Oma
Xusteonosaurus
Eeahosaurus
Toreonosaurus Iteration: 8000, Loss: 24.070350 Onxusichepriuon
Kilabersaurus
Lutrodon
Omaaerosaurus
Xutrcheps
Edaksoje
Trodiktonus Iteration: 10000, Loss: 23.844446 Onyusaurus
Klecalosaurus
Lustodon
Ola
Xusodonia
Eeaeosaurus
Troceosaurus Iteration: 12000, Loss: 23.291971 Onyxosaurus
Kica
Lustrepiosaurus
Olaagrraiansaurus
Yuspangosaurus
Eealosaurus
Trognesaurus Iteration: 14000, Loss: 23.382338 Meutromodromurus
Inda
Iutroinatorsaurus
Maca
Yusteratoptititan
Ca
Troclosaurus Iteration: 16000, Loss: 23.255630 Meustolkanolus
Indabestacarospceryradwalosaurus
Justolopinaveraterasauracoptelalenyden
Maca
Yusocles
Daahosaurus
Trodon Iteration: 18000, Loss: 22.905483 Phytronn
Meicanstolanthus
Mustrisaurus
Pegalosaurus
Yuskercis
Egalosaurus
Tromelosaurus Iteration: 20000, Loss: 22.873854 Nlyushanerohyisaurus
Loga
Lustrhigosaurus
Nedalosaurus
Yuslangosaurus
Elagosaurus
Trrangosaurus Iteration: 22000, Loss: 22.710545 Onyxromicoraurospareiosatrus
Liga
Mustoffankeugoptardoros
Ola
Yusodogongterosaurus
Ehaerona
Trododongxernochenhus Iteration: 24000, Loss: 22.604827 Meustognathiterhucoplithaloptha
Jigaadosaurus
Kurrodon
Mecaistheansaurus
Yuromelosaurus
Eiaeropeeton
Troenathiteritaus Iteration: 26000, Loss: 22.714486 Nhyxosaurus
Kola
Lvrosaurus
Necalosaurus
Yurolonlus
Ejakosaurus
Troindronykus Iteration: 28000, Loss: 22.647640 Onyxosaurus
Loceahosaurus
Lustleonlonx
Olabasicachudrakhurgawamosaurus
Ytrojianiisaurus
Eladon
Tromacimathoshargicitan Iteration: 30000, Loss: 22.598485 Oryuton
Locaaesaurus
Lustoendosaurus
Olaahus
Yusaurus
Ehadopldarshuellus
Troia Iteration: 32000, Loss: 22.211861 Meutronlapsaurus
Kracallthcaps
Lustrathus
Macairugeanosaurus
Yusidoneraverataus
Eialosaurus
Troimaniathonsaurus Iteration: 34000, Loss: 22.447230 Onyxipaledisons
Kiabaeropa
Lussiamang
Pacaeptabalsaurus
Xosalong
Eiacoteg
Troia
Conclusion
You can see that your algorithm has started to generate plausible dinosaur names towards the end of the training. At first, it was generating random characters, but towards the end you could see dinosaur names with cool endings. Feel free to run the algorithm even longer and play with hyperparameters to see if you can get even better results. Our implemetation generated some really cool names like maconucon, marloralus and macingsersaurus. Your model hopefully also learned that dinosaur names tend to end in saurus, don, aura, tor, etc.
If your model generates some non-cool names, don't blame the model entirely--not all actual dinosaur names sound cool. (For example, dromaeosauroidesis an actual dinosaur name and is in the training set.) But this model should give you a set of candidates from which you can pick the coolest!
This assignment had used a relatively small dataset, so that you could train an RNN quickly on a CPU. Training a model of the english language requires a much bigger dataset, and usually needs much more computation, and could run for many hours on GPUs. We ran our dinosaur name for quite some time, and so far our favoriate name is the great, undefeatable, and fierce: Mangosaurus!


4 - Writing like Shakespeare
The rest of this notebook is optional and is not graded, but we hope you'll do it anyway since it's quite fun and informative.
A similar (but more complicated) task is to generate Shakespeare poems. Instead of learning from a dataset of Dinosaur names you can use a collection of Shakespearian poems. Using LSTM cells, you can learn longer term dependencies that span many characters in the text--e.g., where a character appearing somewhere a sequence can influence what should be a different character much much later in ths sequence. These long term dependencies were less important with dinosaur names, since the names were quite short.

Let's become poets!
We have implemented a Shakespeare poem generator with Keras. Run the following cell to load the required packages and models. This may take a few minutes.
from __future__ import print_function
from keras.callbacks import LambdaCallback
from keras.models import Model, load_model, Sequential
from keras.layers import Dense, Activation, Dropout, Input, Masking
from keras.layers import LSTM
from keras.utils.data_utils import get_file
from keras.preprocessing.sequence import pad_sequences
from shakespeare_utils import *
import sys
import io
Using TensorFlow backend.
Loading text data...
Creating training set...
number of training examples: 31412
Vectorizing training set...
Loading model...
To save you some time, we have already trained a model for ~1000 epochs on a collection of Shakespearian poems called "The Sonnets".
Let's train the model for one more epoch. When it finishes training for an epoch---this will also take a few minutes---you can run generate_output, which will prompt asking you for an input (<40 characters). The poem will start with your sentence, and our RNN-Shakespeare will complete the rest of the poem for you! For example, try "Forsooth this maketh no sense " (don't enter the quotation marks). Depending on whether you include the space at the end, your results might also differ--try it both ways, and try other inputs as well.
print_callback = LambdaCallback(on_epoch_end=on_epoch_end)
model.fit(x, y, batch_size=128, epochs=1, callbacks=[print_callback])
Epoch 1/1
31412/31412 [==============================] - 264s - loss: 2.0210
<keras.callbacks.History at 0x7f1e8788ed30>
# Run this cell to try with different inputs without having to re-train the model
generate_output()
Write the beginning of your poem, the Shakespeare machine will complete it. Your input is: Forsooth this maketh no sense Here is your poem: Forsooth this maketh no sensed
dede in not by to beauth of of my borind,
that infoul be't ploa geat of lusk this, hove you mo)sb your of mr neme
wathar thou woetant shall now eye but yet,
that thy aded chould excwin of the love thee sres that me.
fol i of wry moran sos yet kindy
nrugh for feal br by waker fich hest of simind,
muke mud wiml labd threnech he ins faven. an love i hes when (hee to poot sley love,
to gray much
The RNN-Shakespeare model is very similar to the one you have built for dinosaur names. The only major differences are:
- LSTMs instead of the basic RNN to capture longer-range dependencies
- The model is a deeper, stacked LSTM model (2 layer)
- Using Keras instead of python to simplify the code
If you want to learn more, you can also check out the Keras Team's text generation implementation on GitHub: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py.
Congratulations on finishing this notebook!
References:
- This exercise took inspiration from Andrej Karpathy's implementation: https://gist.github.com/karpathy/d4dee566867f8291f086. To learn more about text generation, also check out Karpathy's blog post.
- For the Shakespearian poem generator, our implementation was based on the implementation of an LSTM text generator by the Keras team: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py
Sequence Models Week 1 Character level language model - Dinosaurus land的更多相关文章
- Sequence Model-week1编程题2-Character level language model【RNN生成恐龙名 LSTM生成莎士比亚风格文字】
Character level language model - Dinosaurus land 为了构建字符级语言模型来生成新的名称,你的模型将学习不同的名字,并随机生成新的名字. 任务清单: 如何 ...
- 课程五(Sequence Models),第一 周(Recurrent Neural Networks) —— 2.Programming assignments:Dinosaur Island - Character-Level Language Modeling
Character level language model - Dinosaurus land Welcome to Dinosaurus Island! 65 million years ago, ...
- Sequence Models
Sequence Models This is the fifth and final course of the deep learning specialization at Coursera w ...
- [C7] Andrew Ng - Sequence Models
About this Course This course will teach you how to build models for natural language, audio, and ot ...
- Coursera, Deep Learning 5, Sequence Models, week2, Natural Language Processing & Word Embeddings
Word embeding 给word 加feature,用来区分word 之间的不同,或者识别word之间的相似性. 用于学习 Embeding matrix E 的数据集非常大,比如 1B - 1 ...
- 课程五(Sequence Models),第三周(Sequence models & Attention mechanism) —— 1.Programming assignments:Neural Machine Translation with Attention
Neural Machine Translation Welcome to your first programming assignment for this week! You will buil ...
- [C5W3] Sequence Models - Sequence models & Attention mechanism
第三周 序列模型和注意力机制(Sequence models & Attention mechanism) 基础模型(Basic Models) 在这一周,你将会学习 seq2seq(sequ ...
- Sequence Models Week 3 Neural Machine Translation
Neural Machine Translation Welcome to your first programming assignment for this week! You will buil ...
- 用CNTK搞深度学习 (二) 训练基于RNN的自然语言模型 ( language model )
前一篇文章 用 CNTK 搞深度学习 (一) 入门 介绍了用CNTK构建简单前向神经网络的例子.现在假设读者已经懂得了使用CNTK的基本方法.现在我们做一个稍微复杂一点,也是自然语言挖掘中很火 ...
随机推荐
- 微信小程序—添加背景音乐
问题: 想在打开小程序时就自动播放背景音乐(循环) 解决方法: 1.思路:写一个函数,在 onLoad()中调用 2. //index.js //获取应用实例 const back = wx.get ...
- 利用 Ruoyi 开发自己的业务管理系统__测试结构完成
前言铺垫不多说 (1)Ruoyi这个平台不错:如果你觉得你比Ruoyi的作者牛逼,你就不用看我这个文章了,你可以走了,因为我自认为比Ruoyi的作者要烂: (2)必须已经成功搭建Ruoyi,并能在自己 ...
- 盘姬工具箱WV1.10
========================================================================== {盘姬工具箱CruiserEXPforWin版是一 ...
- C++ mfc 简易文本编辑器 遇到的一些问题
[题目40]简易文本编辑器. 设计一个简易的文本编辑器. 设计要求: (1) 具有图形菜单界面: (2) 查找,替换(等长,不等长),插入(插串,文本块的插入).文本块移动(行块,列块移动),删除; ...
- JuJu团队12月3号工作汇报
JuJu团队12月3号工作汇报 JuJu Scrum 团队成员 今日工作 剩余任务 困难 于达 修改batch里给sentence加padding的方法 继续调试 无 婷婷 给crossentro ...
- Python基础week1
本节内容 Python介绍 发展史 Python 2 or 3? 安装 Hello World程序 变量 用户输入 模块初识 .pyc是个什么鬼? 数据类型初识 数据运算 表达式if ...else语 ...
- js数据类型 判断
1. js数据类型(两种数据类型) 基本数据类型:null undefined number boolean symbol string 引用数据类型: array object null: 空对象 ...
- lvm 通过扩容本身磁盘容量扩容
场景:sdb之前是3G容量,现在扩容了sdb的容量到8G.现在把新扩容的5G容量扩展到现有的逻辑卷中 [root@localhost ~]# pvresize /dev/sdb Physical v ...
- 004、mysql使用SHOW语句找出服务器上当前存在什么数据库
SHOW DATABASES; 不忘初心,如果您认为这篇文章有价值,认同作者的付出,可以微信二维码打赏任意金额给作者(微信号:382477247)哦,谢谢.
- Java 逆序打印链表
递归 package cookie; public class PrintListReversal { public void reversalOut(Node head) { if (head != ...
