CGAL代码阅读跳坑指南

CGAL代码阅读跳坑指南

整体框架介绍

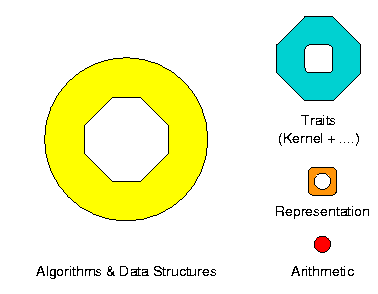
CGAL中的算法和数据结构由它们使用的对象类型和操作参数化。它们可以处理满足特定语法和语义需求的任何具体模板参数。为了避免长参数列表，参数类型被收集到一个单独的类中，称为CGAL中的traits类。Concept是由一组需求定义的类型的抽象。概念是由一组需求定义的类型的抽象。如果任何具体类型满足与概念相对应的一组需求，则称为这个概念对应的Model。使用这个术语，我们可以说CGAL算法或数据结构带有一个traits概念，并且可以与这个概念的任何具体traits模型一起使用。

CGAL定义了geometry kernel的概念。理想情况下，这个概念的任何模型都可以与任何CGAL算法一起使用。当然，只有当一个算法或数据结构对其traits类的需求被核心概念所包含时，也就是说，如果一个算法或数据结构没有核心概念定义中未涵盖的特殊需求，这种情况才成立。目前，CGAL提供了一个基本geometry kernel的概念，它定义了各种几何对象，如点、线段、直线、圆和对它们的操作，以及另外两个概念，circular kernel和spherical kernel。最后两个内核的目标是在平面上的圆和圆弧上指定一大组功能（circular kernel），并为生活在三维球体上的圆、圆弧（spherical kernel）指定类似的功能。

CGAL目前为CGAL 2D和3D内核概念提供了几个模型，为2D圆形和3D球形内核概念提供了一个模型。。它们再次被参数化，并且在几何对象的表示和所涉及类型的可交换性方面有所不同。在前四种情况下，内核由数字类型参数化，数字类型用于存储坐标，决定内核原语的基本算法。

在最后两种情况下，圆核和球核也由Algebraic Kernel参数化，这与代数基础一起，是CGAL中第三个明显的高阶泛化。CGAL中的代数基础是表示代数结构的一组概念，由传统代数中著名的对应概念驱动。代数基础决定每个代数结构的运算、它们的属性（例如，它们是精确的还是近似的）以及它们之间的互操作性。Algebraic Kernel负责为CGAL算法中使用的geometry kernel或特征类所需的代数操作提供抽象。目标是能够构造、比较和执行多项式方程的实根运算。根据用于确定根的多项式的变量数量，有不同的概念（目前有单变量和双变量代数核的概念），以及针对库的特定几何高层（如圆形和球形核）的专门概念。这些概念每个概念至少有一个模型。

CGAL中还有更多的互补层。最基本的层是配置层。此层负责根据安装期间运行的测试的结果设置配置标志。支持库层在支持库手册中有文档记录，其中包含处理CGAL中的可视化、数字类型、流和STL扩展等内容的包。

以上内容是对官方文档中介绍的翻译，见：https://doc.cgal.org/latest/Manual/devman_intro.html#secoverall_design

个人理解

Traits、Concept：都是用来定义一组满足特定语法和语义需求的概念（参数类型的集合）；

Model：是对于这些参数类型的实现，对Kernel进行一定的封装；

Kernel：是最终概念具体实现的地方；

Algorithm：指的是利用概念提供的信息，完成对应的实现；

示例分析

下面以https://doc.cgal.org/latest/Convex_hull_2/classCGAL_1_1Convex__hull__traits__2.html为例验证上面的理解是不是有问题的，下面不考虑算法到底是怎么实现的。

Concepts

https://doc.cgal.org/latest/Convex_hull_2/classConvexHullTraits__2.html

定义中说明了convex hull and extreme point算法被参数化为Traits类，定义了算法需要的对象和判断的方法。其中类型主要包括：Point_2, Equal_2, Less_xy_2, Less_yx_2, Left_turn_2, Less_signed_distance_to_line_2, Less_rotate_ccw_2, Orientation_2；需要的方法有：拷贝构造函数，Equal_2 equal_2_object(), Less_xy_2 less_xy_2_object(), Less_yx_2 less_yx_2_object(), Less_signed_distance_to_line_2 less_signed_distance_to_line_2_object (), Less_rotate_ccw_2 less_rotate_ccw_2_object(), Left_turn_2 left_turn_2_object(), Orientation_2 orientation_2_object()。

Model

CGAL::Convex_hull_constructive_traits_2
CGAL::Convex_hull_traits_2<R>
CGAL::Convex_hull_traits_adapter_2<R>
CGAL::Projection_traits_xy_3<K>
CGAL::Projection_traits_yz_3 <K>
CGAL::Projection_traits_xz_3<K>

代码示例（仅使用kernel）

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/ch_graham_andrew.h>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_2 Point_2;
int main()
{
  CGAL::set_ascii_mode(std::cin);
  CGAL::set_ascii_mode(std::cout);
  std::istream_iterator< Point_2 >  in_start( std::cin );
  std::istream_iterator< Point_2 >  in_end;
  std::ostream_iterator< Point_2 >  out( std::cout, "\n" );
  CGAL::ch_graham_andrew( in_start, in_end, out );
  return 0;
}

ch_graham_andrew提供了两个接口，如下：

// With out traits
template <class InputIterator, class OutputIterator>
inline
OutputIterator
ch_graham_andrew( InputIterator  first,
                  InputIterator  last,
                  OutputIterator result );
// With traits
template <class InputIterator, class OutputIterator, class Traits>
OutputIterator
ch_graham_andrew( InputIterator  first,
                  InputIterator  last,
                  OutputIterator result,
                  const Traits&  ch_traits );

那么就需要详细看下Kernel的实现，此处直看偏特化为true的情况：

class Epick
  : public Filtered_kernel_adaptor<
               Type_equality_wrapper< Simple_cartesian<double>::Base<Epick>::Type, Epick >, true >
{};

typedef Epick Exact_predicates_inexact_constructions_kernel;

首先看一下最内层Simple_cartesian<double>::Base<Epick>::Type对应的是：Cartesian_base_no_ref_count<double,Epick>，于是得到

class Epick
  : public Filtered_kernel_adaptor<
               Type_equality_wrapper< Cartesian_base_no_ref_count<double,Epick>, Epick >, true >
{};

Epick最后的基类是：Cartesian_base，该基类定义了Point_2, Vector_2等数据结构，如下 ：

typedef PointC2<Kernel>                             Point_2;
typedef VectorC2<Kernel>                            Vector_2;
typedef DirectionC2<Kernel>                         Direction_2;
/// ...

PointC2，Vector2，DirectionC2等是可以找到具体实现的。其他的概念中对应的类型和函数的实现见：

template < typename FT_, typename Kernel_ >
struct Cartesian_base_no_ref_count
  : public Cartesian_base< Kernel_, FT_ >
{
    typedef FT_                                           RT;
    typedef FT_                                           FT;

    // The mechanism that allows to specify reference-counting or not.
    template < typename T >
    struct Handle { typedef T   type; };

    template < typename Kernel2 >
    struct Base { typedef Cartesian_base_no_ref_count<FT_, Kernel2>  Type; };

    typedef Kernel_ K;
#define CGAL_Kernel_pred(Y,Z) typedef CartesianKernelFunctors::Y<K> Y; \
                              Y Z() const { return Y(); }
#define CGAL_Kernel_cons(Y,Z) CGAL_Kernel_pred(Y,Z)

#include <CGAL/Kernel/interface_macros.h>
};

#include <CGAL/Kernel/interface_macros.h> 定义了概念中对应的函数，类型，具体如下：

CGAL_Kernel_pred(Less_signed_distance_to_line_2,
                 less_signed_distance_to_line_2_object)
CGAL_Kernel_pred(Equal_2,
		 equal_2_object)
CGAL_Kernel_pred(Less_xy_2,
		 less_xy_2_object)
CGAL_Kernel_pred(Less_yx_2,
		 less_yx_2_object)
CGAL_Kernel_pred(Less_signed_distance_to_line_2,
                 less_signed_distance_to_line_2_object)
CGAL_Kernel_pred(Less_rotate_ccw_2,
		 less_rotate_ccw_2_object)
CGAL_Kernel_pred(Left_turn_2,
                 left_turn_2_object)
CGAL_Kernel_pred_RT(Orientation_2,
		    orientation_2_object)
// ...

上面的定义都可以通过下面的宏进行展开：

#define CGAL_Kernel_pred(Y,Z) typedef CartesianKernelFunctors::Y<K> Y; \
                              Y Z() const { return Y(); }

CartesianKernelFunctors中定义了各种概念上具体的Functor类型，这些Functor提供了一些辅助的几何关系计算的功能，同时这些类型的实现是由Cartesian_base中对应的类型组装而成的。

template <class InputIterator, class OutputIterator>
inline
OutputIterator
ch_graham_andrew( InputIterator  first,
                  InputIterator  last,
                  OutputIterator result )
{
    typedef std::iterator_traits<InputIterator>   ITraits;
    typedef typename ITraits::value_type          value_type;  // Kernel::Point_2
    typedef CGAL::Kernel_traits<value_type>       KTraits;     //
    typedef typename KTraits::Kernel              Kernel;      // Kernel
    return ch_graham_andrew( first, last, result, Kernel());
}

算法内部中利用了kernel中依据概念提供的数据结构和辅助函数。

代码示例（使用Traits）

对应的示例代码如下：

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/convex_hull_2.h>
#include <CGAL/Convex_hull_traits_adapter_2.h>
#include <CGAL/property_map.h>
#include <vector>
#include <numeric>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_2 Point_2;
typedef CGAL::Convex_hull_traits_adapter_2<K,
          CGAL::Pointer_property_map<Point_2>::type > Convex_hull_traits_2;
int main()
{
  std::vector<Point_2> points = { Point_2(10,0),
                                  Point_2(3,4),
                                  Point_2(0,0),
                                  Point_2(10,10),
                                  Point_2(2,6) };

  std::vector<std::size_t> indices(points.size()), out;
  std::iota(indices.begin(), indices.end(),0);

  CGAL::convex_hull_2(indices.begin(), indices.end(), std::back_inserter(out),
                      Convex_hull_traits_2(CGAL::make_property_map(points)));
  for( std::size_t i : out){
    std::cout << "points[" << i << "] = " << points[i] << std::endl;
  }
  return 0;
}

先来认识下：CGAL::make_property_map：

template <class T>
struct Pointer_property_map{
  typedef boost::iterator_property_map< T*,
                              boost::typed_identity_property_map<std::size_t>,
                              T,
                              T&> type; ///< mutable `LvaluePropertyMap`
  typedef boost::iterator_property_map< const T*,
                              boost::typed_identity_property_map<std::size_t>,
                              T,
                              const T&> const_type; ///< non-mutable `LvaluePropertyMap`
};

template <class T>
inline
typename Pointer_property_map<T>::type
make_property_map(T* pointer)
{
  return typename Pointer_property_map<T>::type(pointer);
}

可见最终会导向：boost::iterator_property_map。简单来讲就是用来将随机访问的迭代器转换成LvaluePropertyMap，该类型提供了operator[]，和get()函数来访问对象。进一步了解可以查找：Boost Property Map Library。

接着看一下：Convex_hull_traits_2(CGAL::make_property_map(points))就是构建了一个traits类。这个traits内部直接实现了concepts中给出的需求，如下：

template<class Base_traits,class PointPropertyMap>
class Convex_hull_traits_adapter_2:public Base_traits{
	typedef typename boost::property_traits<PointPropertyMap>::key_type Point_2;
    struct Less_xy_2 : public Base_traits::Less_xy_2{
        Less_xy_2(const PointPropertyMap& ppmap,const typename Base_traits::Less_xy_2& base):
        Base_traits::Less_xy_2(base),ppmap_(ppmap){}
        const PointPropertyMap& ppmap_;
        bool operator()(Arg_type p,Arg_type q) const {
            return static_cast<const typename Base_traits::Less_xy_2*>(this)->operator()(get(ppmap_,p),get(ppmap_,q));
        }
    };

    struct Equal_2 : public Base_traits::Equal_2{ ... }
    //...
    Equal_2 equal_2_object () const {return Equal_2(ppmap_,static_cast<const Gt*>(this)->equal_2_object() );}
    Left_turn_2 left_turn_2_object () const {return Left_turn_2(ppmap_,static_cast<const Gt*>(this)->left_turn_2_object() );}
    //...

这里的Base_traits就是对应上面示例中的的Kernel。以Less_xy_2为例，operator()最后调用的是：

static_cast<const typename Base_traits::Less_xy_2*>(this)->operator()(get(ppmap_,p),get(ppmap_,q));

这里就有完美的切换到了Kernel的实现中到了。

But，为什么么要这么设计，这么实现呢？这个我就不懂了。。，希望大家一起探索下。。

小结

针对相关代码的阅读，可以先理解concept中对应的数据类型和函数。然后再看对应的算法实现。看算法实现的时候，就不用过多关注kernel中和concept相关的内容了，更多的关注算法实现的过程即可。不然代码跳来跳去很快就会晕晕乎乎了。