bzoj4481非诚勿扰（期望dp）

有n个女性和n个男性。每个女性的如意郎君列表都是所有男性的一个子集，并且可能为空。如果列表非空，她们会在其中选择一个男性作为自己最终接受的对象。将“如意郎君列表”中的男性按照编号从小到大的顺序呈现给她。对于每次呈现，她将独立地以P的概率接受这个男性（换言之，会以1−P的概率拒绝这个男性）。如果她选择了拒绝，App就会呈现列表中下一个男性，以此类推。如果列表中所有的男性都已经呈现，那么会重新按照列表的顺序来呈现这些男性，直到她接受了某个男性为止。显然，在这种规则下，每个女性只能选择接受一个男性，而一个男性可能被多个女性所接受。当然，也可能有部分男性不被任何一个女性接受。这样，每个女性就有了自己接受的男性（“如意郎君列表”为空的除外）。现在考虑任意两个不同的、如意郎君列表非空的女性a和b，如果a的编号比b的编号小，而a选择的男性的编号比b选择的编号大，那么女性a和女性b就叫做一对不稳定因素。求得不稳定因素的期望个数（即平均数目）

Solution

此题要求期望的逆序对数，我们先分析每个男性在每个女性的选择中被选择的概率（图是网上抄来的）

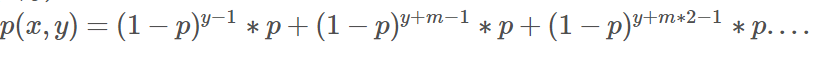
等比数列求和一下

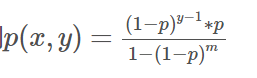
概率求出来了，我们就可以以男性编号为下标，维护一个树状数组，里面的值代表这个男性在前面出现的期望次数。

求出这个后，我们在乘上当前男性被选择的概率就可以成为答案的一部分。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#define N 500002
using namespace std;
typedef long double ld;
ld ans,tr[N],p;
int n,m;
struct zzh{
    int x,y;
}a[N];
bool cmp(zzh a,zzh b){
    if(a.x!=b.x)return a.x<b.x;
    else return a.y<b.y;
}
void add(int x,ld y){while(x<=n)tr[x]+=y,x+=x&-x;}
double query(int x){double ans=;while(x)ans+=tr[x],x-=x&-x;return ans;}
int main(){
//    freopen("4481.in","r",stdin);
//    freopen("4481.out","w",stdout);
    scanf("%d%d%Lf",&n,&m,&p);
    for(int i=;i<=m;++i)scanf("%d%d",&a[i].x,&a[i].y);
    sort(a+,a+m+,cmp);
    int now=;
    for(int i=now;i<=m;i=now+){
        now=i;
        while(a[now].x==a[now+].x)now++;
        ld x=;
        for(int j=i;j<=now;++j)x*=(-p);x=-x;
        ld y=p;
        for(int j=i;j<=now;++j){
            ld xx=y/x;
            add(n-a[j].y+,xx);
            ans+=xx*query(n-a[j].y);
            y*=(-p);
        }
    }
    printf("%.2Lf",ans);
    return ;
}