机器学习---朴素贝叶斯分类器（Machine Learning Naive Bayes Classifier）

朴素贝叶斯分类器是一组简单快速的分类算法。网上已经有很多文章介绍，比如这篇写得比较好：https://blog.csdn.net/sinat_36246371/article/details/60140664。在这里，我按自己的理解再整理一遍。

在机器学习中，我们有时需要解决分类问题。也就是说，给定一个样本的特征值（feature₁,feature₂,...feaure_n），我们想知道该样本属于哪个分类标签（label₁,label₂,...label_n）。即：我们想要知道该样本各个标签的条件概率P(label|features)是多少，这样我们就可以知道该样本属于哪个分类。例如：假设数据集一共有2个分类（标签），如果现在出现一个新的样本，其P(label₁|feature_sample)>P(label₂|feature_sample)，那么我们就可以判定该样本的标签为label₁。

那么P(label|feature)该如何计算呢？如果数据是离散值，那么P(label|feature)可以计算出来。但是如果总体数据非常之多，我们不可能一个一个去观测记录下来，只能随机取样，通过样本来对总体进行估计。又或者如果数据是连续值呢？因此我们可以通过假设训练集数据{(feature₁,label₁), (feature₂,label₂), ...(feature_n,label_n)}的分布（按假设的分布生成这些数据，这也是为什么朴素贝叶斯分类器是生成模型的原因），学习其分布参数，对P(label|feature)进行估计。

有以下三种估计方法，分别是：极大似然估计法（MLE），贝叶斯估计法（Bayesian），极大后验概率估计法（MAP）。（图片摘自：https://www.cnblogs.com/little-YTMM/p/5399532.html）

（一）极大似然估计法（MLE, maximum likelihood estimation）

属于频率学派，认为存在唯一真值θ。

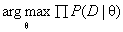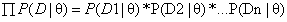如果我们对总体进行取样，我们假设取样出的数据符合某一种分布（比如说正态分布），但是我们不知道这个分布的参数θ（比如说平均值，标准差)，极大似然估计法就是去找到能使模型产生出样本数据的概率最大的参数θ，也就是找到。由于有连乘运算，通常对似然函数取对数计算，就可以把连乘变成求和，然后求导，取导数为0的极值点，就是想找的参数值。

但是极大似然估计只适用于数据量大的情况。如果数据量较小，结果很可能会产生偏差。举个简单的例子，假如把一个均匀的硬币抛10次，有7次正面朝上，3次反面朝上（假设数据服从beta分布）。那么这个beta分布函数就是，函数在x=0.7时达到最大。那么我们能说P(Head)=0.7吗？这个结果肯定不准，因为我们都知道P(Head)=P(Tail)=0.5。但是如果我们把这个硬币抛1000次，得出的结果就会较准确了。但是现实中，很多时候，我们无法做那么多次试验。对此，解决的办法就是贝叶斯估计法。

（二）贝叶斯估计法（Bayesian estimation）

属于贝叶斯学派，认为θ是一个随机变量，符合一定的概率分布。

还是对总体进行取样，我们假设取样出的数据符合某一种分布，而且根据以往的经验，我们知道参数θ的概率分布（P(θ)也即先验概率），我们根据贝叶斯定理得到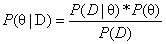，这样通过学习条件概率P(D|θ)的分布，就可以计算出后验概率P(θ|D)的分布。对新样本预测时考虑所有可能的θ，所以可以得到最优的预测结果。

还是用上面抛硬币的例子，我们仍然假设数据服从beta分布，而且我们知道每次抛硬币服从二次分布（即：根据经验，抛10次硬币，应该有5次正面朝上，5次反面朝上），通过这个先验知识，我们可以计算得出后验概率P(Head|D)，也就是P(Head)的beta函数为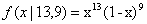，我们将可能的参数（概率从0-1）代入，计算可知beta函数在x=0.6时达到峰值（可参见这篇文章： http://www.360doc.com/content/17/1002/23/31429017_691875200.shtml）。通过加入先验概率，我们得出的预测结果要更准确。这说明，贝叶斯估计可以用于数据量较少或者比较稀疏的情况。

然而，我们发现贝叶斯估计法虽然解决了数据量较少的问题，但是又带来了新的问题。因为在用贝叶斯估计法解决问题的时候，我们让参数θ服从某种概率密度函数分布，这就会导致计算过程高度复杂。人们为了计算上的方便，就提出不再把所有的后验概率p(θ|D)都找出来，而是仍然采用类似于极大似然估计的思想，找到极大后验概率，这种简单有效的方法叫做极大后验概率估计法。

（三）极大后验概率估计法（MAP, maximum a posterior probability estimation）

极大后验概率估计法与极大似然估计法类似，只是加入了先验概率P(θ)，相当于增加一种惩罚（正则化），以减少偏差。

（注：如果先验概率P(θ)是均匀分布的，那么极大后验概率估计法等价于极大似然估计法。）

下面，我来推导一下极大后验概率估计法的整个过程：

根据贝叶斯定理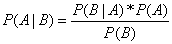：，我们把数据集的特征（features）和标签（label）代入其中得到： 。

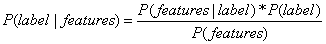由于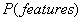是常量（constant），该公式可改写成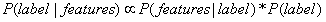：。（∝表示成正比）

朴素贝叶斯假设各特征之间相互独立，于是就有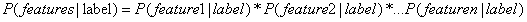。（注：朴素贝叶斯之所以被称为“朴素”，就是因为它假设各个特征之间相互独立。）

此时，公式可写成：。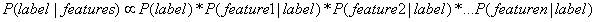

也即：。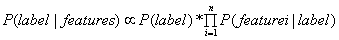

这就是说：我们学习了先验概率P(label)和条件概率P(features|label)的分布，得到P(features,label)的联合分布，就可以推导出后验概率P(label|features)的分布。

（注：）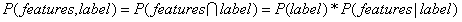

现在我们不想知道后验概率P(label|features)的分布，因此我们用极大似然估计法对条件概率P(features|label)进行估计，然后得到对后验概率P(label|features)的最好估计：。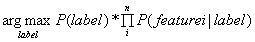

也就是说，朴素贝叶斯分类器把样本分到后验概率P(label|featurees)最大的分类当中。

（需要注意的是：某个新样本的某一特征可能在训练集中从未出现过，其条件概率P(features|label)会变为0，这样就会导致P(label|features)也为0，这显然是不对的。解决办法是引入拉普拉斯平滑（Laplace Smoothing）。例如在对文本进行分类时，我们将某个字出现的频率视为一个特征，用极大似然估计法估计其条件概率P(features|label)就是：在某个分类（label）里，这个字出现的频率/（除以）所有字出现的频率。而引入拉普拉斯平滑（Laplace Smoothing）后，对其条件概率P(features|label)的估计就变为：(在某个分类（label）里，这个字出现的频率+1)/(所有字出现的频率+类别数量）。这样，当训练集数据量充分大时，并不会对结果产生影响，并且解决了频率为0的问题。）

这里再总结一下，极大后验概率估计法与贝叶斯估计法的区别在于：极大后验概率估计法是用极大似然估计法对条件概率进行估计，估计出条件概率的最大值，从而找到后验概率的最大值；而贝叶斯估计法是假设先验概率服从某种分布，计算出所有可能的后验概率，也就是说找出后验概率的分布。

根据对数据集P(features|label)分布的不同假设，朴素贝叶斯分类器可分为不同的类型，以下是三种常见的类型：

1. 高斯朴素贝叶斯（Gaussian Naive Bayes）   ---  假设特征是连续值，且符合高斯分布。公式： 

2. 多项式朴素贝叶斯（Multinomial Naive Bayes）   ---   假设特征向量由多项式分布生成。公式：

3. 伯努利朴素贝叶斯（Bernoulli Naive Bayes）   ---   假设特征是独立的布尔（二进制变量）类型。公式：

优点：1. 训练和预测的速度非常快（由于假设每个特征相互独立，因此每个条件概率P(feature|label)的分布可以独立地被一维分布估计出来）

2. 容易解释

3. 可调参数少

4. 尽管朴素贝叶斯模型对特征之间相互独立这一假设在实际应用中往往不成立，但其分类效果仍然不错

缺点：1. 由于朴素贝叶斯分类器对数据分布有严格的假设，因此它的预测效果通常比复杂模型差

适用于：1. 各个类别的区分度很高

2. 维度非常高的数据集

3. 为分类问题提供快速粗糙的基本方案

经典应用：文档分类（document classification），垃圾邮件过滤（spam filtering）