支持向量机（SVM）：用一条线分开红豆与绿豆

算法原理

要找到一些线，这些线都可以分割红豆和绿豆，找到正确的方向或者斜率的那条线，确认马路的宽度，得到最优解--马路的中轴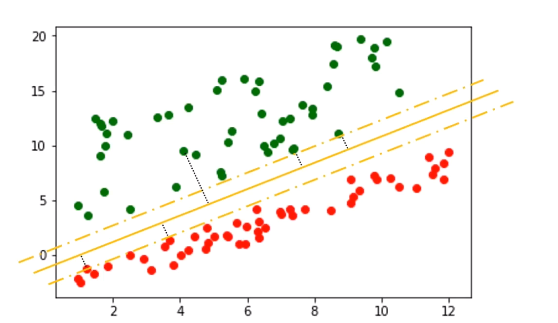

超平面：在三维空间中，平面是两个点距离相同的点的轨迹。一个平面没有厚度，而且可以把空间分割成两部分。超平面是在维度大于三维度的时候仍然满足上面的条件，而且它的自由度比空间维度小1。（通俗讲，在二维中就是直线，三维就是平面，在三维以上的就是超平面）

支持向量：假设找到一条线可以可以分割红豆和绿豆，红豆和绿豆中距离这条线最近的几个样本点被称为支持向量。这些点到这条线的距离叫间隔。

注意：在决定最佳超平面时只有支持向量起作用，而其他数据点并不起作用

如何处理不清晰的边界

软间隔：在这个间隔区域里允许出现一定数量的样本，这个间隔为软间隔

硬间隔：划分非常清晰，在间隔中间没有任何红豆和绿豆的理想状态下，这个间隔为硬间隔

如何处理非线性可分

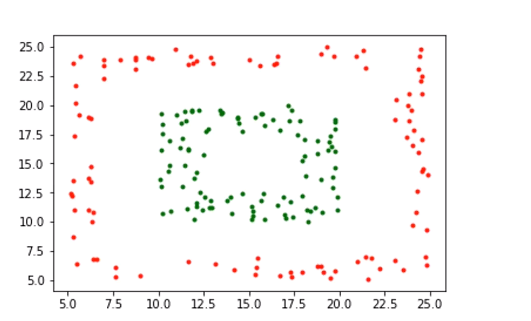
svm采取的办法：把不可划分的样本映射到高维空间。借助“核函数”来映射到高维的操作

常见的核函数：线性核函数、多项式核函数、高斯核函数

算法优点

1.有严格的数学理论支持，可解释性强（能得到全局最优解）

2.算法的鲁棒性很好（指控制系统在一定（结构，大小）的参数摄动下，维持其它某些性能的特性）【支持向量没问题就没问题】

算法缺点

1.训练集所需要的资源很大（只能处理小数据集比如几千条）

2.只能处理二分类问题

3.模型预测时，预测时间与支持向量个数成正比

#SVM
from sklearn import datasets #sklearn的数据集
from sklearn import svm #引入svm包
import numpy as np #矩形运算库numpy

np.random.seed(0)
#设置随机种子，不设置的话默认是按系统时间作为参数，设置后可以保证我们每次产生的随机数是一样的

iris = datasets.load_iris() #获取鸢尾花数据集
iris_x = iris.data #数据部分
iris_y = iris.target #类别部分

#从150条数据中选取140条作为训练集，10条作为测试集。permutation接收一个数作为参数（这里为数据集长度150），
#产生一个0-149乱序一维数组
indices = np.random.permutation(len(iris_x))
iris_x_train = iris_x[indices[:-10]]  #训练集数据
iris_y_train = iris_y[indices[:-10]]  #训练集标签
iris_x_test = iris_x[indices[-10:]]   #测试集数据
iris_y_test = iris_y[indices[-10:]]   #测试集数据

#使用线性核SVC是分类支持向量机的意思，另外还有SVR是回归支持向量机
clf = svm.SVC(kernel='linear')

#调用该对象的训练方法，主要接收两个参数：训练数据集及其类别标签
clf.fit(iris_x_train,iris_y_train) #拟合

#调用该对象的测试方法，主要接收一个参数：测试数据集
iris_y_predict = clf.predict(iris_x_test)

#调用该对象的打分方法，计算出准确率
score = clf.score(iris_x_test,iris_y_test,sample_weight=None)

#输出测试结果
print('iris_y_predict=')
print(iris_y_predict)

#输出原始测试数据集的正确标签，以方便对比
print('iris_y_test=')
print(iris_y_test)

#输出准确率计算结果
print('Accuracy:',score)