最简单的离散概率分布，伯努利分布 《考研概率论学习之我见》 -by zobol

上文讲了离散型随机变量的分布，我们从最简单的离散型分布伯努利分布讲起，伯努利分布很简单，但是在现实生活中使用的很频繁。很多从事体力工作的人，在生活中也是经常自觉地“发现”伯努利分布，它很容易理解。

1.为什么要先从伯努利分布来学？

2.在生活中什么样的事情可能服从伯努利分布？

3.伯努利实验的三条性质

4.生活中的伯努利实验

5.伯努利分布的函数及其图像

6.伯努利分布的数学期望

7伯努利分布的方差

1.为什么要先从伯努利分布来学？

离散型随机变量对应的概率函数都是离散函数，其中很多离散函数是很复杂的。有一些可以看做是连续函数的离散型，有一些则根本找不到任何规律。而伯努利分布的函数图像是最简单的，就两个点，我们从最简单的开始学。

2.在生活中什么样的事情可能服从伯努利分布？

如果一个事情可以被简单分为两个结果，且概率和为1那么就可以服从伯努利分布。（可以说，真的很方便了，任何事情只要可以被简单看做1和0，就服从伯努利分布）

3.伯努利实验的三条性质

所谓伯努利实验就是指服从伯努利分布的实验，它具有三条性质：（1）可重复（2）两个种结果（3）概率和为1

只要现实世界中的事情符合伯努利实验的三个性质，那么它的发生概率分布就一定服从伯努利分布。

4.生活中的伯努利实验

（1）硬币掉落

（2）生男生女

（3）扔骰子，点数为6和不为6（不要求等概率）

（4）做判断题正确还是错误

可以想象到，因为不限制等概率，生活的中绝大多数事件都可以看做是伯努利实验，不过注意伯努利实验还有第三条实验就是可以重复也就是重复事件互为独立事件，它们都服从伯努利分布。(雅克-伯努利就是在研究独立重复事件中发现的伯努利分布)

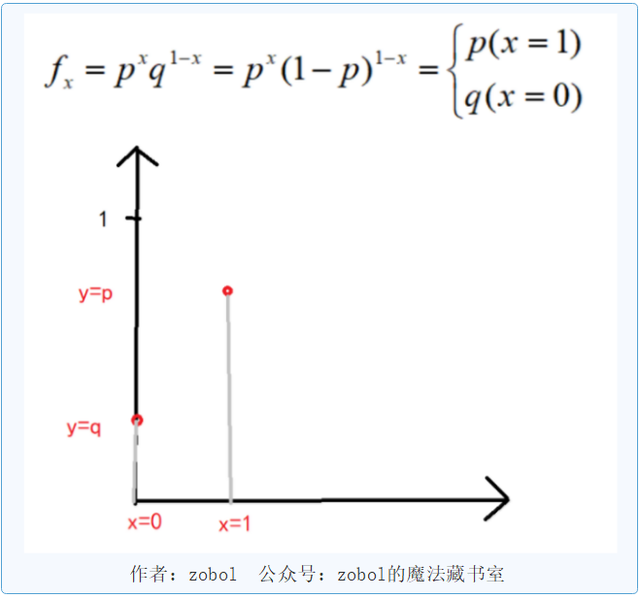
5.伯努利分布的函数及其图像

概率质量函数，设成功概率为p,失败概率为q=1-p,定义域x为{1,0}

6.伯努利分布的数学期望

根据数学期望的计算公式即可，因为x就两个值，其中一个还是0，很好计算、

、

数学期望等于p，也就是说每次伯努利实验最可能取得到的值是p,但是伯努利实验的结果只能是1和0。似乎这个数学期望没什么用，等到了n重伯努利分布之后，这个数学期望p才能有用处。

7伯努利分布的方差

计算方差有两个公式都可以的：

我们可以得到对于任何伯努利分布，它的方差都是在[0,1/4]的区间上。