【LeetCode动态规划#02】图解不同路径I + II（首次涉及二维dp数组，）

不同路径

力扣题目链接(opens new window)

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 2, n = 3
输出：3

解释：从左上角开始，总共有 3 条路径可以到达右下角。

向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

思路

题意没什么好分析的，就是从起始点到终点有多少种走法

直接上五部曲分析

五步走

1、确定dp数组含义

从题干和所给示例可以得出

dp[i][j]:从[0] [0]出发走到[i] [j]有dp[i][j]种走法

2、确定递推公式

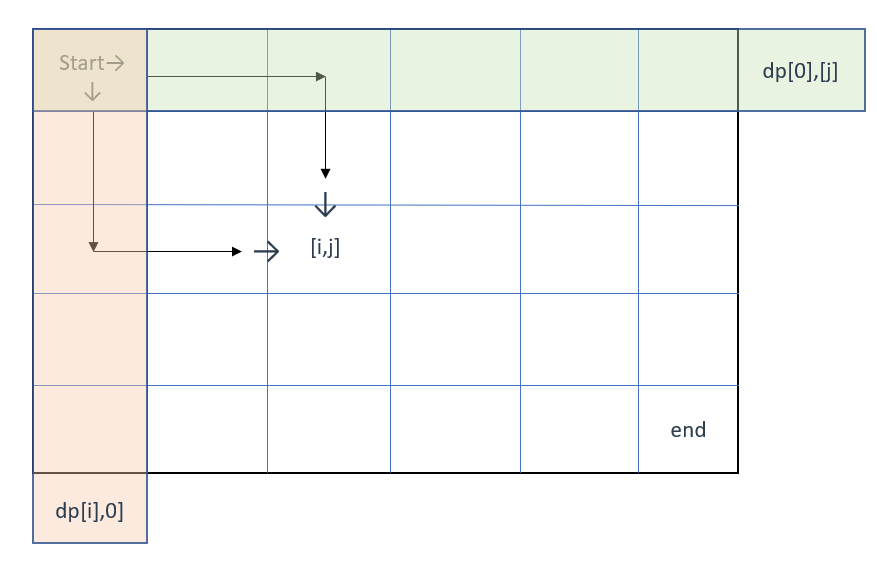
如图所示

根据dp数组的定义，

从[0] [0]出发走到[i] [j]上方（也就是[i] [j-1]）有dp[i][j-1]种走法，其再往下走一步就可以到[i] [j]（即等于dp[i][j]）

从[0] [0]出发走到[i] [j]左侧（也就是[i-1] [j]）有dp[i-1][j]种走法，其再往右走一步就可以到[i] [j]

（注意，以dp[i][j-1]为例，它指的是走法而不是走了几步，因此再往下走，不是dp[i][j-1] + 1）

因为题目说了每次只能向下或向左移动一步，所以上面的分析就已经把所有到达[i] [j]的可能路径表示出来了

即到达[i] [j]的路径种类等于从其上方到达的方式加上从其左边到达的方式

也就是：dp[i][j] = dp[i][j-1] + dp[i-1][j]

3、确定dp数组初始化方式

dp[i][j-1]是到达[i] [j]上方的所有路径，那么其一定使用了最上方部分（绿色）

同理，在推导dp[i-1][j]时也使用到了最左侧的部分（橙色）

那么，这两块区域就是我们要初始化的对象，即dp[0],[j]和dp[i],[0]

那么，初始值是多少呢？

还是联系dp数组的定义，我们发现，在最上方的绿色部分前进时，无论在哪一格、怎么走都只有一种方式前进（就是往右）

（因为题目规定只能往右或下走）

橙色的部分同理

因此绿色和橙色部分的每一个格子的dp值其实都是1，意味着不论从这两个区域中的哪一格出发，都只有一种前进方式

所以可以把dp[0],[j]和dp[i],[0]全部初始化为1

for (int i = 0; i < m; i++) dp[i][0] = 1;

for (int j = 0; j < n; j++) dp[0][j] = 1;

4、确定遍历方式

因为只能往右或者下走，那前进顺序就是从左往右或者从上到下了

自然的，这也就是遍历的顺序

这样，在从左往右时，遍历的每一个格才能利用左边的上一个格来进行推导，从上到下同理

代码

这里创建的dp数组是二维的，结构如下：(举例)

m行->（[0,0,0,0]为一行）

[[0,0,0,0], n列↓

 [0,0,0,0],

 [0,0,0,0],

 [0,0,0,0]，

 [0,0,0,0]]

class Solution {

public:

    int uniquePaths(int m, int n) {

        //定义dp数组(先使用0初始化数组)

        vector<vector<int>> dp(m, vector<int>(n, 0));

        //初始化dp[i][0]和dp[0][j]

        for(int i = 0; i < m; ++i) dp[i][0] = 1;

        for(int j = 0; j < n; ++j) dp[0][j] = 1;

        //遍历

        for(int i = 1; i < m; ++i){//[0,0]已经初始化了，因此i、j都需要从1开始

           for(int j = 1; j < n; ++j){

               dp[i][j] = dp[i][j - 1] + dp[i - 1][j];//递推公式

           }

        }

        return dp[m - 1][n - 1];//注意，这里需要减1，因为数组是从0开始数的，而mn是从1开始的

    }

};

不同路径II

力扣题目链接(opens new window)

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

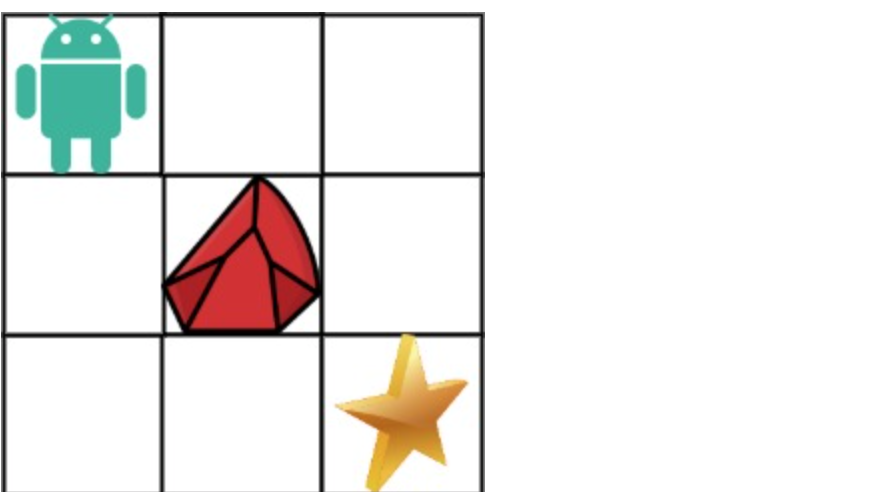
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2 解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i] [j] 为 0 或 1

思路

这题是在上题的基础上增加了障碍物，主要区别在状态转换方程和dp数组初始化上

并且需要注意的是，本题是直接给了网格并在上面注明类障碍物的位置（0无障碍，1有障碍）

直接开始

五步走

1、确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2、确定递推公式

这里递推公式的核心部分和上题一样，但是需要增加额外的条件

当遇到障碍时，障碍后面的路径就没有办法走到了，因此需要保持为0

if(obstacleGrid[i][j] == 0){//没遇到障碍物时就正常计算dp数组的值

    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

}

3、确定dp数组初始化方式

因为引入了障碍，初始化方式会有所变化

还是拿之前的图来看

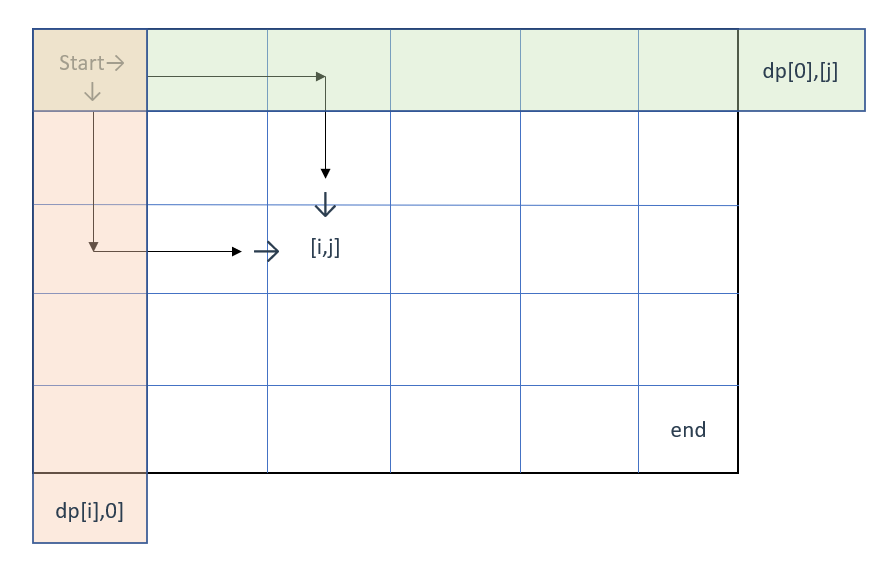
如果绿色和橙色部分（需要初始化的地方）有障碍物，那么从障碍物起，之后的位置都将标记为0，因为那些地方再也去不到了

（因为只能往右或下走）

于是初始化时需要加入条件

在上一题中，我们给出的初始化代码为：

vector<vector<int>> dp(m, vector<int>(n, 0));//初始值为0

if(int i = 0; i < m; ++i) dp[i][0] = 1;

if(int j = 0; j < n; ++j) dp[0][j] = 1;

本题中需要在for循环的结束条件中做改动

vector<vector<int>> dp(m, vector<int>(n, 0));//初始值为0

if(int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) dp[i][0] = 1;

if(int j = 0; j < n && obstacleGrid[0][j] == 0; ++j) dp[0][j] = 1;

即在初始化绿色部分时，如果没遇到障碍物，正常初始化赋值；如果遇到了，就终止for循环，之后的位置保持值为0

（橙色部分同理）

4、确定遍历顺序

仍然是从左到右、从上到下，但在遍历过程中如果遇到障碍物，需要continue一下

for(int i = 0; i < m; ++i){

    for(int j = 0; j < n; ++j){

        if(obstacleGrid[i][j] == 1) continue;

        dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

    }

}

5、打印dp数组

因为本题的逻辑相较于上题复杂了一些，所以有必要自己推算一下dp数组来确保结果的正确性

用示例1举例：

dp数组手动推导如图所示

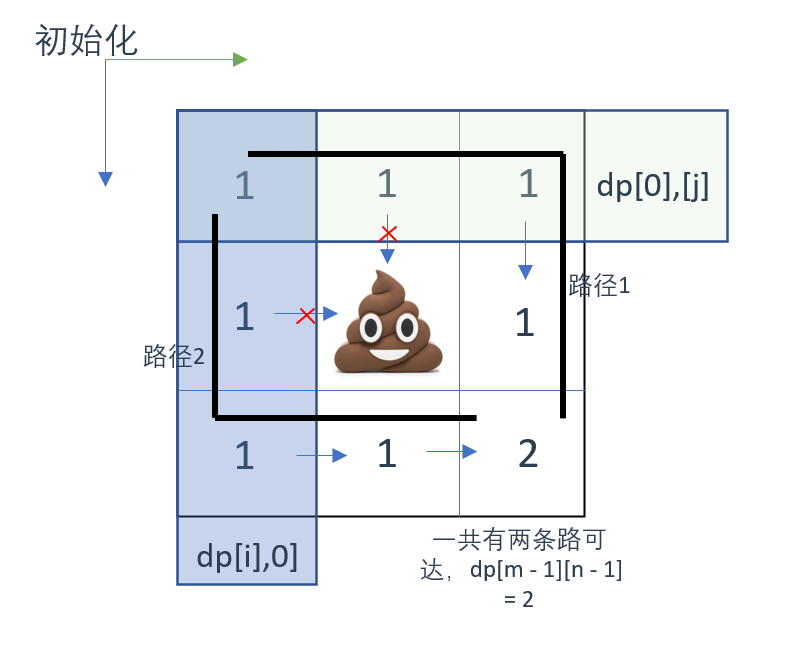
完整代码

class Solution {

public:

    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {

        //创建dp数组

        int m = obstacleGrid.size();

        int n = obstacleGrid[0].size();

        //如果在起点/终点出现障碍，直接返回0

        if(obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return 0;

        vector<vector<int>> dp(m, vector<int>(n, 0));

        //初始化dp数组

        for(int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) dp[i][0] = 1;

        for(int j = 0; j < n && obstacleGrid[0][j] == 0; ++j) dp[0][j] = 1;

        //遍历

        for(int i = 1; i < m; ++i){

            for(int j = 1; j < n; ++j){

                if(obstacleGrid[i][j] == 1) continue;

                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

            }

        }

        return dp[m - 1][n - 1];

    }

};

注意：复制某些重复代码时，记得要修改完所有的对应值！！！