论文解读(MERIT)《Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning》
论文信息
论文标题:Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning
论文作者:Ming Jin, Yizhen Zheng, Yuan-Fang Li, Chen Gong, Chuan Zhou, Shirui Pan
论文来源:2021, IJCAI
论文地址:download
论文代码:download
1 Introduction
创新:融合交叉视图对比和交叉网络对比。
2 Method
算法图示如下:
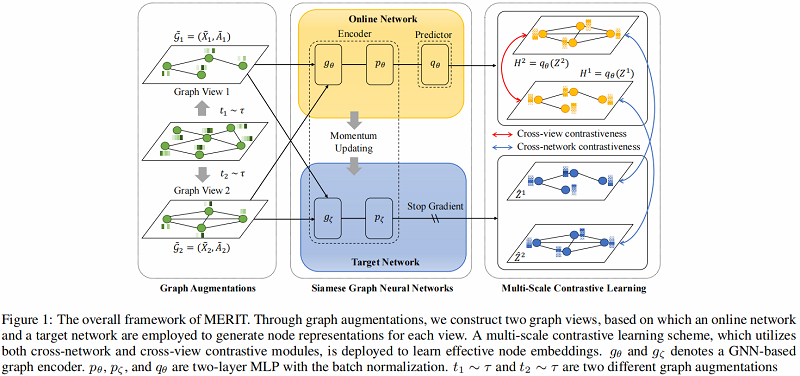
模型组成部分:
- Graph augmentations
- Cross-network contrastive learning
- Cross-view contrastive learning
2.1 Graph Augmentations
- Graph Diffusion (GD)
$S=\sum\limits _{k=0}^{\infty} \theta_{k} T^{k} \in \mathbb{R}^{N \times N}\quad\quad\quad(1)$
这里采用 PPR kernel:
$S=\alpha\left(I-(1-\alpha) D^{-1 / 2} A D^{-1 / 2}\right)^{-1}\quad\quad\quad(2)$
- Edge Modification (EM)
给定修改比例 $P$ ,先随机删除 $P/2$ 的边,再随机添加$P/2$ 的边。(添加和删除服从均匀分布)
- Subsampling (SS)
在邻接矩阵中随机选择一个节点索引作为分割点,然后使用它对原始图进行裁剪,创建一个固定大小的子图作为增广图视图。
- Node Feature Masking (NFM)
给定特征矩阵 $X$ 和增强比 $P$,我们在 $X$ 中随机选择节点特征维数的 $P$ 部分,然后用 $0$ 掩码它们。
在本文中,将 SS、EM 和 NFM 应用于第一个视图,并将 SS+GD+NFM 应用于第二个视图。
2.2 Cross-Network Contrastive Learning
MERIT 引入了一个孪生网络架构,它由两个相同的编码器(即 $g_{\theta}$, $p_{\theta}$, $g_{\zeta}$ 和 $p_{\zeta}$)组成,在 online encoder 上有一个额外的预测器$q_{\theta}$,如 Figure 1 所示。
这种对比性的学习过程如 Figure 2(a) 所示:

其中:
- $H^{1}=q_{\theta}\left(Z^{1}\right)$
- $Z^{1}=p_{\theta}\left(g_{\theta}\left(\tilde{X}_{1}, \tilde{A}_{1}\right)\right)$
- $Z^{2}=p_{\theta}\left(g_{\theta}\left(\tilde{X}_{2}, \tilde{A}_{2}\right)\right)$
- $\hat{Z}^{1}=p_{\zeta}\left(g_{\zeta}\left(\tilde{X}_{1}, \tilde{A}_{1}\right)\right)$
- $\hat{Z}^{2}=p_{\zeta}\left(g_{\zeta}\left(\tilde{X}_{2}, \tilde{A}_{2}\right)\right)$
参数更新策略(动量更新机制):
$\zeta^{t}=m \cdot \zeta^{t-1}+(1-m) \cdot \theta^{t}\quad\quad\quad(3)$
其中,$m$、$\zeta$、$\theta$ 分别为动量参数、target network 参数和 online network 参数。
损失函数如下:
$\mathcal{L}_{c n}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left(\mathcal{L}_{c n}^{1}\left(v_{i}\right)+\mathcal{L}_{c n}^{2}\left(v_{i}\right)\right)\quad\quad\quad(6)$
其中:
$\mathcal{L}_{c n}^{1}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, \hat{z}_{v_{i}}^{2}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, \hat{z}_{v_{j}}^{2}\right)\right)}}\quad\quad\quad(4) $
$\mathcal{L}_{c n}^{2}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{2}, \hat{z}_{v_{i}}^{1}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{2}, \hat{z}_{v_{j}}^{1}\right)\right)}}\quad\quad\quad(5) $
2.3 Cross-View Contrastive Learning
损失函数:
$\mathcal{L}_{c v}^{k}\left(v_{i}\right)=\mathcal{L}_{\text {intra }}^{k}\left(v_{i}\right)+\mathcal{L}_{\text {inter }}^{k}\left(v_{i}\right), \quad k \in\{1,2\}\quad\quad\quad(10)$
其中:
$\mathcal{L}_{c v}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left(\mathcal{L}_{c v}^{1}\left(v_{i}\right)+\mathcal{L}_{c v}^{2}\left(v_{i}\right)\right)\quad\quad\quad(9)$
$\mathcal{L}_{\text {inter }}^{1}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{j}}^{2}\right)\right)}}\quad\quad\quad(7) $
$\begin{aligned}\mathcal{L}_{i n t r a}^{1}\left(v_{i}\right) &=-\log \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)}{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)+\Phi} \\\Phi &=\sum\limits_{j=1}^{N} \mathbb{1}_{i \neq j} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{j}}^{1}\right)\right)\end{aligned}\quad\quad\quad(8)$
2.4 Model Training
$\mathcal{L}=\beta \mathcal{L}_{c v}+(1-\beta) \mathcal{L}_{c n}\quad\quad\quad(11)$
3 Experiment
数据集
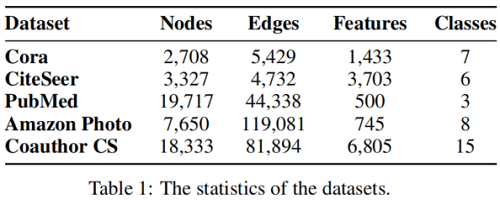
基线实验
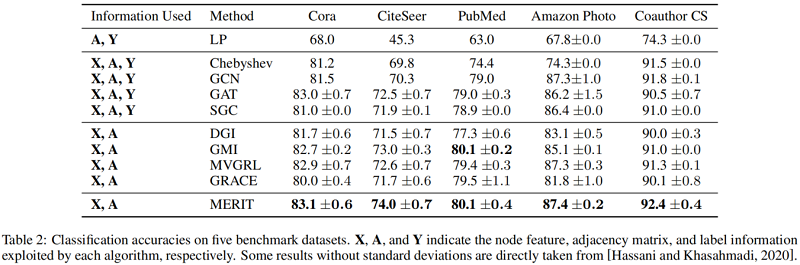
论文解读(MERIT)《Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning》的更多相关文章
- 论文解读(SUBG-CON)《Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning》
论文信息 论文标题:Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning论文作者:Yizhu Ji ...
- 论文解读(GMI)《Graph Representation Learning via Graphical Mutual Information Maximization》2
Paper Information 论文作者:Zhen Peng.Wenbing Huang.Minnan Luo.Q. Zheng.Yu Rong.Tingyang Xu.Junzhou Huang ...
- 论文解读(GMI)《Graph Representation Learning via Graphical Mutual Information Maximization》
Paper Information 论文作者:Zhen Peng.Wenbing Huang.Minnan Luo.Q. Zheng.Yu Rong.Tingyang Xu.Junzhou Huang ...
- 论文解读(GRCCA)《 Graph Representation Learning via Contrasting Cluster Assignments》
论文信息 论文标题:Graph Representation Learning via Contrasting Cluster Assignments论文作者:Chun-Yang Zhang, Hon ...
- 论文解读GALA《Symmetric Graph Convolutional Autoencoder for Unsupervised Graph Representation Learning》
论文信息 Title:<Symmetric Graph Convolutional Autoencoder for Unsupervised Graph Representation Learn ...
- 论文解读(SUGRL)《Simple Unsupervised Graph Representation Learning》
Paper Information Title:Simple Unsupervised Graph Representation LearningAuthors: Yujie Mo.Liang Pen ...
- 论文阅读 Dynamic Graph Representation Learning Via Self-Attention Networks
4 Dynamic Graph Representation Learning Via Self-Attention Networks link:https://arxiv.org/abs/1812. ...
- 论文解读(MVGRL)Contrastive Multi-View Representation Learning on Graphs
Paper Information 论文标题:Contrastive Multi-View Representation Learning on Graphs论文作者:Kaveh Hassani .A ...
- 论文笔记:Deeper and Wider Siamese Networks for Real-Time Visual Tracking
Deeper and Wider Siamese Networks for Real-Time Visual TrackingUpdated on 2019-04-01 16:10:37 Paper ...
随机推荐
- seqlist template
1 #include <iostream.h> 2 typedef int ElemType; 3 typedef struct{ 4 ElemType *elem; 5 int leng ...
- 团队vue基础镜像选择思考
前端镜像可以考虑使用nginx或者openresty; 镜像 大小 说明 nginx:1.20.2-alpine 8.41 MB 最小最新版本 nginx:1.21.4 50.95 MB 最新版本 n ...
- redis之 主从复制和哨兵(一)
一.Redis主从复制 主从复制:主节点负责写数据,从节点负责读数据,主节点定期把数据同步到从节点保证数据的一致性 1. 主从复制的相关操作 a,配置主从复制方式一.新增redis6380.conf, ...
- Jquery是什么?有什么作用?
Jquery是继prototype之后又一个优秀的Javascrīpt框架.它是轻量级的js库(压缩后只有21k) ,它兼容CSS3,还兼容各种浏览器 (IE 6.0+, FF 1.5+, Safar ...
- SpringBoot和SpringCloud?
SpringBoot是Spring推出用于解决传统框架配置文件冗余,装配组件繁杂的基于Maven的解决方案,旨在快速搭建单个微服务而SpringCloud专注于解决各个微服务之间的协调与配置,服务之间 ...
- kafka 分布式(不是单机)的情况下,如何保证消息的顺序消费?
Kafka 分布式的单位是 partition,同一个 partition 用一个 write ahead log 组织, 所以可以保证 FIFO 的顺序.不同 partition 之间不能保证顺序. ...
- MariaDB 存储引擎一览(官方文档翻译)
inline-translate.translate { } inline-translate.translate::before, inline-translate.translate::after ...
- Linux分区问题
一.基本分区的作用及其大小 /boot分区: 存放引导文件和Linux内核文件等. 引导文件:判断启动哪一个操作系统或启动哪个内核. 内核:管理硬件和软件资源,程序与硬件之间的桥梁. 分区大小:100 ...
- 学习Docker(一)
一.docker介绍 docker是半虚拟化,比完全虚拟化性能高,可以使用物理机性能100% Docker 镜像(Images): 用于创建 Docker 容器的模板 Docker 容器(Contai ...
- Vue报错之"[Vue warn]: Avoid mutating a prop directly since the value will be overwritten whenever the parent component re-renders. Instead......"
一.报错截图 [Vue warn]: Avoid mutating a prop directly since the value will be overwritten whenever the p ...
