Cot

题目大意

两种操作

给坐标上一个直角三角形中每个整点权值$+1$

求坐标上一个直角三角形中每个整点权值之和

题解

一顿分析思考加推导之后，发现并不存在这样的数据结构(大概是有，只是我不知道)，于是考虑分块暴力。

我们记录两个前缀和

$p_{x,y}$表示$(x,y)$点权

$R_{x,y}=\sum\limits_{i=1}^{x}\sum\limits_{j=1}^{\min(y,i)}p_{i,j}$
$T_{x,y}=\sum\limits_{i=x-y+1}^{x}\sum\limits_{j=1}^{\min(y,i)}p_{i,j}$

形象化的就长这样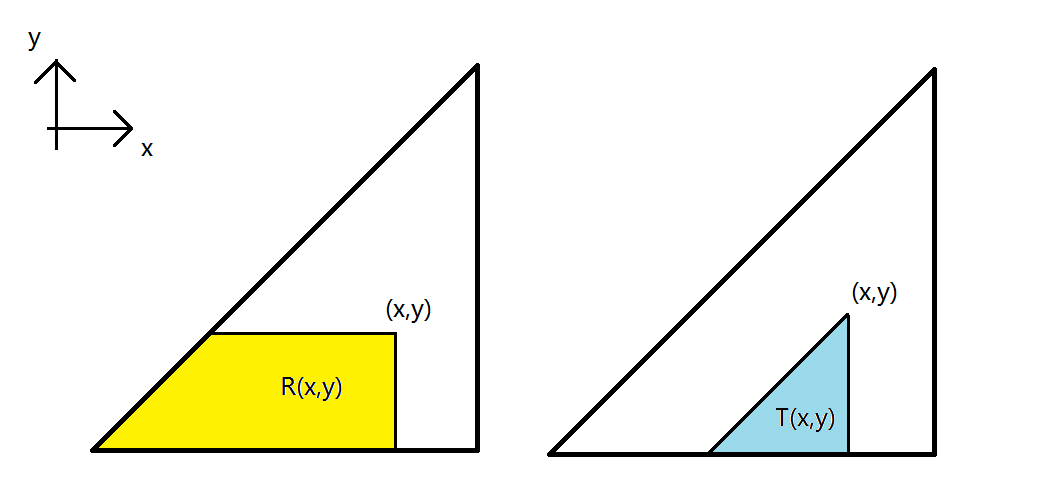

于是我们可以通过这两个前缀和加上简单的容斥解决任意一个三角形的和。

修改这样的，考虑差分

对修改数进行分块，设块长为$B$，则对于每次修改，我们考虑对平面打差分表记，你会发现如果利用朴素二维前缀和的计算方式差分每个点的值会很麻烦，直接考虑对于每一个$x$维护$y$从小到大的的话标记会是这样(红色的是要整体$+1$的三角形)

这样做一次是$O(N)$，虽然能过，不过这个$O(N)$可以变成O$(1)$的。我们对于差分的标记进行查分，维护一个从左向右的差分和从左下到右上的差分即可。

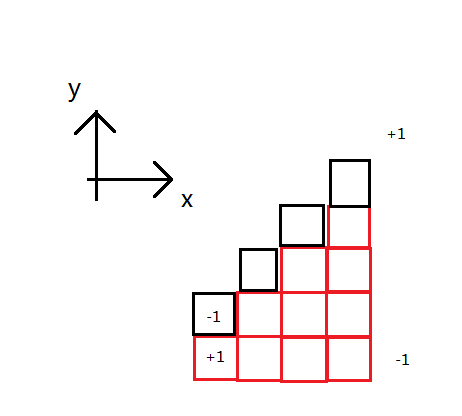
然后对于每$B$次修改，我们直接暴力重构一边当前的$T,R$，即先扫一遍差分标记的差分标记，然后差分出点的值，再更新$T,R$。对于每次询问，我们用之前修改过的整块的答案$O(1)$算出来三角形的值，再扫一遍最近的不到$B$次的修改，两个三角形面积$O(1)$求交更新答案即可。

不妨设修改询问均为$Q$次，则复杂度为$O(N^2\frac QB+Q\cdot B)$。

不难发现，当$B$取$N$时，复杂度会严格优于$O(QN)$。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define M 1010
#define BC 2500
#define mid ((l+r)>>1)
using namespace std;
LL read(){
    LL nm=0,fh=1; char cw=getchar();
    for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
    for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');
    return nm*fh;
}
const int n=read();
int tg1[M][M],tg2[M][M],p1[M][M],p2[M][M],qx[M<<2],qy[M<<2],qd[M<<2],cnt;
int F[M][M],val[M][M];
LL R[M][M],T[M][M];
void solve(){
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            p1[i][j]+=p1[i-1][j],p2[i][j]+=p2[i-1][j-1];
            F[i][j]=F[i][j-1]+p1[i][j]+p2[i][j],val[i][j]+=F[i][j];
            R[i][j]=R[i-1][j]+R[i][j-1]-R[i-1][j-1],R[i][j]+=val[i][j];
            T[i][j]=T[i-1][j-1]+R[i][j-1]-R[i-1][j-1],T[i][j]+=val[i][j];
        }
    }
    memset(p1,0,sizeof(p1));
    memset(p2,0,sizeof(p2));
}
LL getans(int x,int y,int k){
    LL sum=0;
    for(int i=1;i<=cnt;i++){
        int flr=max(y,qy[i]),rs=min(x+k-1,qx[i]+qd[i]-1);
        int ctx=max(x-y,qx[i]-qy[i]); LL len=rs-(ctx+flr)+1;
        if(len>0) sum+=((len*(len+1))>>1);
    } return sum;
}
int main(){
    for(int tpe,x,y,dt,Q=read();Q;Q--){
        tpe=read(),x=read(),y=read(),dt=read();
        if(tpe==1){
            ++cnt,qx[cnt]=x,qy[cnt]=y,qd[cnt]=dt;
            p1[x][y]++,p1[x+dt][y]--,p2[x][y+1]--,p2[x+dt][y+dt+1]++;
            if(cnt==BC) solve(),cnt=0; continue;
        }
        LL ans=T[x+dt-1][y+dt-1]-T[x-1][y-1];
        ans-=R[x+dt-1][y-1]-R[x-1][y-1];
        ans+=getans(x,y,dt),printf("%lld\n",ans);
    }
    return 0;
}