Codeforces Round #260 (Div. 2) A , B , C 标记，找规律 ， dp

A. Laptops

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

One day Dima and Alex had an argument about the price and quality of laptops. Dima thinks that the more expensive a laptop is, the better it is. Alex disagrees. Alex thinks that there are two laptops, such that the price of the first laptop is less (strictly smaller) than the price of the second laptop but the quality of the first laptop is higher (strictly greater) than the quality of the second laptop.

Please, check the guess of Alex. You are given descriptions of n laptops. Determine whether two described above laptops exist.

Input

The first line contains an integer n (1 ≤ n ≤ 105) — the number of laptops.

Next n lines contain two integers each, ai and bi (1 ≤ ai, bi ≤ n), where ai is the price of the i-th laptop, and bi is the number that represents the quality of the i-th laptop (the larger the number is, the higher is the quality).

All ai are distinct. All bi are distinct.

Output

If Alex is correct, print "Happy Alex", otherwise print "Poor Alex" (without the quotes).

Examples

input

2
1 2
2 1

output

Happy Alex

题意：第一个数为价格，第二个数为质量， 问是否有质量比另一件好，价格比另一件低的；

思路：因为ai跟bi都不同，所以直接标记，即是a有序，扫一遍就是；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
const int N=1e5+,M=4e6+,inf=1e9+;
int flag[N];
int main()
{
    int x,y,z,i,t;
    scanf("%d",&x);
    for(i=;i<=x;i++)
    {
        int y,z;
        scanf("%d%d",&y,&z);
        flag[y]=z;
    }
    int maxx=flag[];
    for(i=;i<=x;i++)
    {
        if(flag[i]<maxx)
        {
            printf("Happy Alex\n");
            return ;
        }
        maxx=flag[i];
    }
    printf("Poor Alex\n");
    return ;
}

B. Fedya and Maths

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Fedya studies in a gymnasium. Fedya's maths hometask is to calculate the following expression:

(1n + 2n + 3n + 4n) mod 5

for given value of n. Fedya managed to complete the task. Can you? Note that given number n can be extremely large (e.g. it can exceed any integer type of your programming language).

Input

The single line contains a single integer n (0 ≤ n ≤ 10105). The number doesn't contain any leading zeroes.

Output

Print the value of the expression without leading zeros.

Examples

input

4

output

4

input

124356983594583453458888889

output

0

Note

Operation x mod y means taking remainder after division x by y.

Note to the first sample:

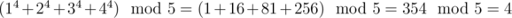
题意：(1^n + 2^n + 3^n + 4^n) mod 5，n是大数；

思路：应该mod5很容易找到规律，写了一发指数循环节；

　　　大数取模：模拟，从前往后遍历一遍就是；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
const int N=1e5+,M=4e6+,inf=1e9+;
char ch[N];
int quickmod(int x,int y,int mod)
{
    int ans=;
    while(y)
    {
        if(y&)ans*=x,ans%=mod;
        y>>=;
        x*=x;
        x%=mod;
    }
    return ans;
}
int main()
{
    int x,y,z,i,t;
    scanf("%s",ch);
    x=strlen(ch);
    int sum=;
    for(i=;i<x;i++)
    {
        sum=sum*+ch[i]-'';
        sum%=;
    }
    int ans=;
    for(i=;i<=;i++)
    ans+=quickmod(i,sum+,);
    printf("%d\n",ans%);
    return ;
}

C. Boredom

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Alex doesn't like boredom. That's why whenever he gets bored, he comes up with games. One long winter evening he came up with a game and decided to play it.

Given a sequence a consisting of n integers. The player can make several steps. In a single step he can choose an element of the sequence (let's denote it ak) and delete it, at that all elements equal to ak + 1 and ak - 1 also must be deleted from the sequence. That step brings ak points to the player.

Alex is a perfectionist, so he decided to get as many points as possible. Help him.

Input

The first line contains integer n (1 ≤ n ≤ 105) that shows how many numbers are in Alex's sequence.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 105).

Output

Print a single integer — the maximum number of points that Alex can earn.

Examples

input

2
1 2

output

2

input

3
1 2 3

output

4

input

9
1 2 1 3 2 2 2 2 3

output

10

Note

Consider the third test example. At first step we need to choose any element equal to 2. After that step our sequence looks like this[2, 2, 2, 2]. Then we do 4 steps, on each step we choose any element equals to 2. In total we earn 10 points.

题意：给你一个n个数，每次可以选择一个数x，得到的贡献是x，需要去掉所有的x+1，跟x-1，求得到的最大贡献；

思路：dp，每个数的贡献显然=该数的值*该数的个数；

　　　dp[i]表示从1-i得到的最大贡献，dp[i]=max(dp[i-1],dp[i-1]+a[i]);a[i]表示i的贡献；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
const int N=1e5+,M=4e6+,inf=1e9+;
ll dp[N];
ll a[N];
int main()
{
    int x,y,z,i,t;
    scanf("%d",&x);
    for(i=;i<=x;i++)
    {
        scanf("%d",&y);
        a[y]+=y;
    }
    dp[]=a[];
    for(i=;i<=1e5;i++)
    dp[i]=max(dp[i-],dp[i-]+a[i]);
    printf("%lld\n",dp[]);
    return ;
}